动态查找树之平衡二叉树Balanced Binary TreeAVL树.docx
《动态查找树之平衡二叉树Balanced Binary TreeAVL树.docx》由会员分享,可在线阅读,更多相关《动态查找树之平衡二叉树Balanced Binary TreeAVL树.docx(21页珍藏版)》请在冰豆网上搜索。
动态查找树之平衡二叉树BalancedBinaryTreeAVL树
动态查找树之平衡二叉树(BalancedBinaryTree,AVL树)
一、平衡二叉树的概念
平衡二叉树(Balancedbinarytree)是由阿德尔森-维尔斯和兰迪斯(Adelson-VelskiiandLandis)于1962年首先提出的,所以又称为AVL树。
定义:
平衡二叉树或为空树,或为如下性质的二叉排序树:
(1)左右子树深度之差的绝对值不超过1;
(2)左右子树仍然为平衡二叉树.
平衡因子BF=左子树深度-右子树深度.
平衡二叉树每个结点的平衡因子只能是1,0,-1。
若其绝对值超过1,则该二叉排序树就是不平衡的。
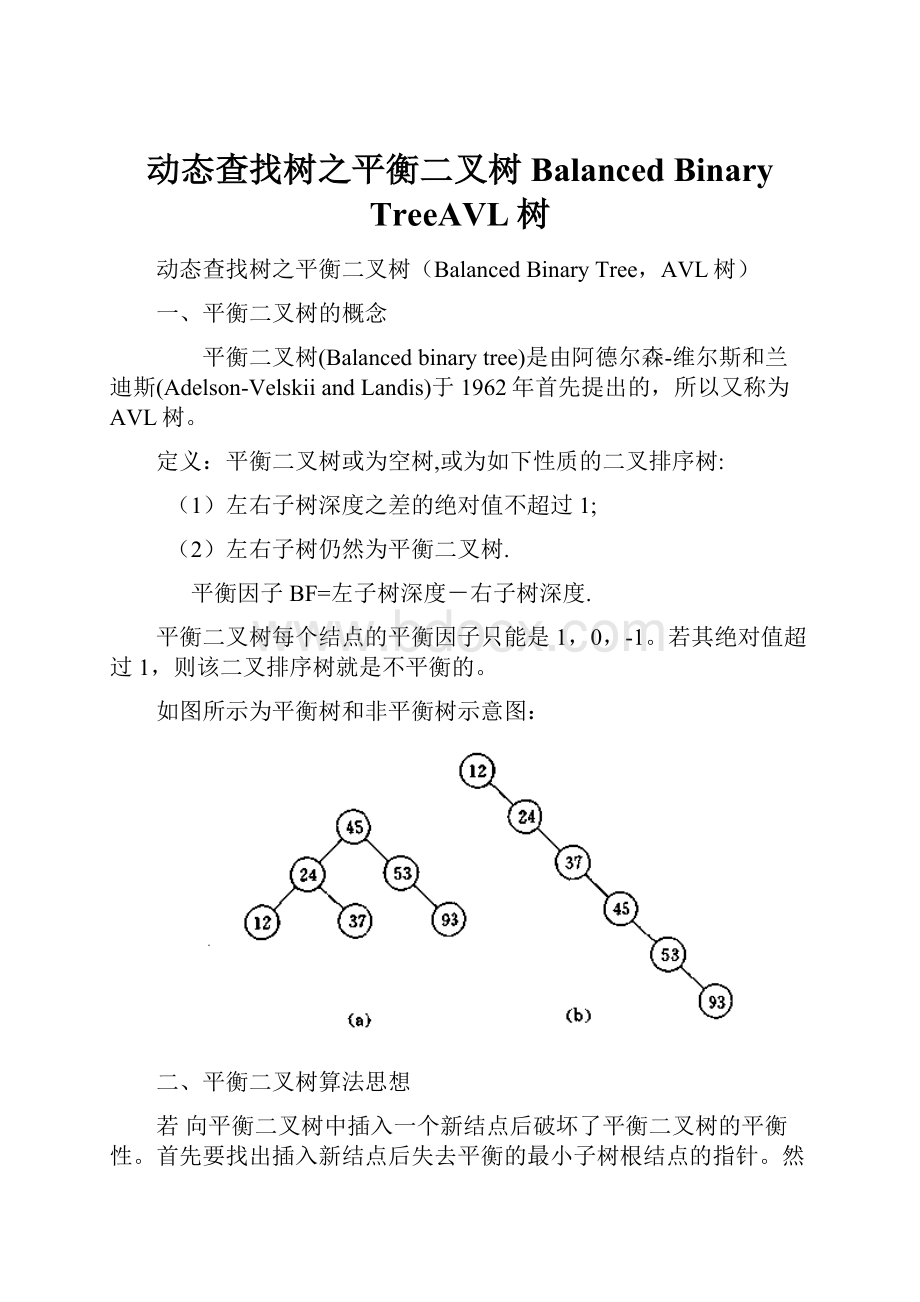
如图所示为平衡树和非平衡树示意图:
二、平衡二叉树算法思想
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
(1)LL型平衡旋转法
由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A作为根结点,A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
(2)RR型平衡旋转法
由于在A的右孩子C的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A作为根结点,A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
(3)LR型平衡旋转法
由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行两次旋转操作(先逆时针,后顺时针)。
即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置,然后再把该D结点向右上旋转提升到A结点的位置。
即先使之成为LL型,再按LL型处理。
如图中所示,即先将圆圈部分先调整为平衡树,然后将其以根结点接到A的左子树上,此时成为LL型,再按LL型处理成平衡型。
(4)RL型平衡旋转法
由于在A的右孩子C的左子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行两次旋转操作(先顺时针,后逆时针),即先将A结点的右孩子C的左子树的根结点D向右上旋转提升到C结点的位置,然后再把该D结点向左上旋转提升到A结点的位置。
即先使之成为RR型,再按RR型处理。
如图中所示,即先将圆圈部分先调整为平衡树,然后将其以根结点接到A的左子树上,此时成为RR型,再按RR型处理成平衡型。
平衡化靠的是旋转。
参与旋转的是3个节点(其中一个可能是外部节点NULL),旋转就是把这3个节点转个位置。
注意的是,左旋的时候p->right一定不为空,右旋的时候p->left一定不为空,这是显而易见的。
如果从空树开始建立,并时刻保持平衡,那么不平衡只会发生在插入删除操作上,而不平衡的标志就是出现bf==2或者bf==-2的节点。
三、二叉排序数的操作及C语言描述
插入删除是互为镜像的操作。
我们可以采用前面对二叉排序树的删除操作来进行。
然后,在删除掉结点后,再对平衡树进行平衡化处理。
删除之所以删除操作需要的平衡化可能比插入时次数多,就是因为平衡化不会增加子树的高度,但是可能会减少子树的高度,在有有可能使树增高的插入操作中,一次平衡化能抵消掉增高;在有可能使树减低的删除操作中,平衡化可能会带来祖先节点的不平衡。
四、二叉排序数的C语言实现
#include"stdio.h"
#include"stdlib.h"
#include"string.h"
#defineLH+1 //左高
#defineEH0 //等高
#defineRH-1 //右高
#defineTRUE1
#defineFALSE1
#defineEQ(a,b)((a)==(b))
#defineLT(a,b)((a)<(b))
#defineLQ(a,b)((a)<=(b))
#defineBT(a,b)((a)>(b))
typedefintKeyType;
typedefintinfo;
typedefintBoolean;
typedefstructElemType
{
KeyTypekey;
//infootherinfo;
};
typedefstructBSTNode
{
ElemTypedata;
intbf;
BSTNode*lchild,*rchild;//左右孩子指针
}BSTNode,*BSTree;
voidR_Rotate(BSTree&p)
{//右旋
BSTreelc;
lc=p->lchild;
p->lchild=lc->rchild;
lc->rchild=p;
p=lc; //p指向新的根结点
}//R_Rotate
voidL_Rotate(BSTree&p)
{//左旋
BSTreerc;
rc=p->rchild;
p->rchild=rc->lchild;
rc->lchild=p;
p=rc; //p指向新的根结点
}//L_Rotate
voidLeftBalance(BSTree&T)
{//作平衡旋转处理
BSTreelc,rd;
lc=T->lchild;
switch(lc->bf)
{
caseLH:
T->bf=lc->bf=EH;
R_Rotate(T);
break;
caseRH:
rd=lc->rchild;
switch(rd->bf)
{
caseLH:
T->bf=RH;lc->bf=EH;break;
caseEH:
T->bf=lc->bf=EH; break;
caseRH:
T->bf=EH;lc->bf=LH;break;
}//switch
rd->bf=EH;
L_Rotate(T->lchild);
R_Rotate(T);
}//switch
}//LeftBalance
voidRightBalance(BSTree&T)
{//作平衡旋转处理
BSTreerc,ld;
rc=T->rchild;
switch(rc->bf)
{
caseRH:
T->bf=rc->bf=EH;
L_Rotate(T);
break;
caseLH:
ld=rc->lchild;
switch(ld->bf)
{
caseLH:
T->bf=LH;rc->bf=EH;break;
caseEH:
T->bf=rc->bf=EH; break;
caseRH:
T->bf=EH;rc->bf=RH;break;
}//switch
ld->bf=EH;
R_Rotate(T->rchild);
L_Rotate(T);
}//switch
}//RightBalance
intInsertAVL(BSTree&T,ElemTypee,int&taller)
{//若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个
//数据元素为e的新结点,并返回1,否则返回0。
若因插入而使二叉排序树
//失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否
if(!
T)
{//插入新结点,树“长高”,置taller为TRUE
T=(BSTree)malloc(sizeof(BSTNode));
T->data=e;
T->lchild=T->rchild=NULL;
T->bf=EH;
taller=TRUE;
}
else
{
ifEQ(e.key,T->data.key)
{//树中已存在和e有相同关键字的结点则不再插入
taller=FALSE;
returnFALSE;
}
ifLT(e.key,T->data.key)
{//应继续在*T的左子树中进行搜索
if(!
InsertAVL(T->lchild,e,taller))//未插入
returnFALSE;
if(taller)// 已插入到*T的左子树中且左子树“长高”
switch(T->bf)//检查*T的平衡度
{
caseLH:
//原本左子树比右子树高,需要作左平衡处理
LeftBalance(T);
taller=FALSE;
break;
caseEH:
//原本左、右子树等高,现因左子树增高而使树增高
T->bf=LH;
taller=TRUE;
break;
caseRH:
T->bf=EH;//原本右子树比左子树高,现左、右子树等高
taller=FALSE;
}
}
else
{//应继续在*T的右子树中进行搜索
if(!
InsertAVL(T->rchild,e,taller))//未插入
returnFALSE;
if(taller)//已插入到T的右子树且右子树“长高”
switch(T->bf)//检查T的平衡度
{
caseLH:
T->bf=EH;//原本左子树比右子树高,现左、右子树等高
taller=FALSE;
break;
caseEH:
//原本左、右子树等高,现因右子树增高而使树增高
T->bf=RH;
taller=TRUE;
break;
caseRH:
//原本右子树比左子树高,需要作右平衡处理
RightBalance(T);
taller=FALSE;
}
}
}
returnTRUE;
}
BSTreeSearchBST(BSTreeT,KeyTypekey)
{//在根指针T所指二叉排序树中递归地查找某关键字等于key的数据元素,
//若查找成功,则返回指向该数据元素结点的指针,否则返回空指针。
if((!
T)||EQ(key,T->data.key))
returnT;//查找结束
elseifLT(key,T->data.key)//在左子树中继续查找
returnSearchBST(T->lchild,key);
else
returnSearchBST(T->rchild,key);//在右子树中继续查找
}//SearchBST
voidDestroyDSTable(BSTree&DT)
{//初始条件:
动态查找表DT存在。
操作结果:
销毁动态查找表DT
if(DT)//非空树
{
if(DT->lchild)//有左孩子
DestroyDSTable(DT->lchild);//销毁左孩子子树
if(DT->rchild)//有右孩子
DestroyDSTable(DT->rchild);//销毁右孩子子树
free(DT);//释放根结点
DT=NULL;//空指针赋0
}//if
}//DestroyDSTable
intInitDSTable(BSTree&DT)
{//操作结果:
构造一个空的动态查找表DT
DT=NULL;
return1;
}//InitDSTable
voidVisit(BSTreeDT)
{
//printf("DT->data.key:
->%d\nT->bf:
%d\n",DT->data.key,DT->bf);
printf("DT->data.key:
->%d\n",DT->data.key);
}//Visit
voidTraverseDSTable(BSTree&DT,void(*Visit)(BSTree))
{//初始条件:
动态查找表DT存在,Visit是对结点操作的应用函数
//操作结果:
按关键字的顺序对DT的每个结点调用函数Visit()一次且至多一次
if(DT)
{
TraverseDSTable(DT->lchild,Visit);//先中序遍历左子树
Visit(DT);//再访问根结点
TraverseDSTable(DT->rchild,Visit);//最后中序遍历右子树
}
}
intInsertAVLD(BSTree&T)
{
ElemTypee;
Booleantaller;
printf("inputthedatauntil-1\n");
scanf("%d",&e.key);
while(e.key!
=-1)
{
InsertAVL(T,e,taller);
printf("inputthedatauntil-1\n");
scanf("%d",&e.key);
}
return1;
}//InsertAVLD
voidLeftBalanceD(BSTreeT,int&shorter)
{
BSTreelc=T->lchild,rd;
switch(lc->bf)
{
caseLH:
T->bf=lc->bf=EH;
R_Rotate(T);break;
caseEH:
T->bf=LH;
lc->bf=RH;
R_Rotate(T);break;
caseRH:
rd=lc->rchild;
switch(rd->bf)
{
caseRH:
T->bf=EH;lc->bf=LH;shorter=0;break;
caseEH:
T->bf=EH;lc->bf=EH;shorter=1;break;
caseLH:
T->bf=RH;lc->bf=EH;shorter=1;break;
}//switch
rd->bf=EH;
L_Rotate(T->lchild);
R_Rotate(T);
}//switch
}//LeftBalanceD
voidRightBalanceD(BSTreeT,int&shorter)
{
BSTreerc=T->rchild,ld;
switch(rc->bf)
{
caseRH:
T->bf=rc->bf=EH;
R_Rotate(T);break;
caseEH:
T->bf=RH;
rc->bf=RH;
L_Rotate(T);shorter=0;break;
caseLH:
ld=rc->lchild;
switch(ld->bf)
{
caseRH:
T->bf=EH;rc->bf=RH;break;
caseEH:
T->bf=EH;rc->bf=EH;break;
caseLH:
T->bf=LH;rc->bf=EH;break;
}//switch
ld->bf=EH;
R_Rotate(T->rchild);
L_Rotate(T);
}//switch
}//RightBalanceD
intSearchBSTD(BSTree&T)
{
ElemTypee;
printf("\npleaseinputthenumberyouwanttosearch:
\n");
scanf("%d",&e.key);
if(SearchBST(T,e.key)!
=NULL)printf("%d",e.key);
elseprintf("failed!
");
return1;
}//SearchBSTD
intDelete(BSTree&T,KeyTypekey,int&shorter)
{
intsuccess=0;//标志成功删除与否
if(T)
{
if(EQ(key,T->data.key))
{//相等,即当前结点就是要删除的结点
if(T->lchild!
=NULL&&T->rchild!
=NULL)
{//要删除结点的左右子树都不空
BSTreeq,r;
//接下来,找到要删除数据的前驱结点,并且将数据与直接前驱
//交换。
这样我们将其前驱删除掉后,再调整平衡树就好了。
q=T->lchild;
r=q;//用r来指向其前驱接点。
while(q)
{
r=q;
q=q->rchild;
}//while(q)
KeyTypetemp=T->data.key;
T->data.key=r->data.key;
r->data.key=temp;
//接下来,在左子树上删除其前驱接点
success=Delete(T->lchild,key,shorter);
if(shorter)
{//由于删除操作导致了树变小了
switch(T->bf)
{
caseLH:
T->bf=EH;break;
caseEH:
T->bf=RH;break;
caseRH:
RightBalanceD(T,shorter);break;
}//switch
}//if
}//if-要删除结点左右子树都不空
else
{//要删除接点有一个子树不为空
BSTreep=T;
T=(T->lchild!
=NULL)?
T->lchild:
T->rchild;
deletep;
success=1;//删除成功
shorter=1;//树变短了。
}//else
}//if=
elseif(LT(key,T->data.key))
{//在左子树上查询要删除的结点
success=Delete(T->lchild,key,shorter);
if(shorter)
{
switch(T->bf)
{
caseLH:
T->bf=EH;shorter=0;break;
caseEH:
T->bf=RH;break;
caseRH:
RightBalanceD(T,shorter);break;
}//switch
}//if-shorter
}//if<
elseif(BT(key,T->data.key))
{//在右子树上查询要删除的结点
success=Delete(T->rchild,key,shorter);
if(shorter)