学年七年级下册数学华东师大新版《第9章 多边形》单元测试题有答案Word文档格式.docx

学年七年级下册数学华东师大新版《第9章 多边形》单元测试题有答案Word文档格式.docx

《学年七年级下册数学华东师大新版《第9章 多边形》单元测试题有答案Word文档格式.docx》由会员分享，可在线阅读，更多相关《学年七年级下册数学华东师大新版《第9章 多边形》单元测试题有答案Word文档格式.docx（13页珍藏版）》请在冰豆网上搜索。

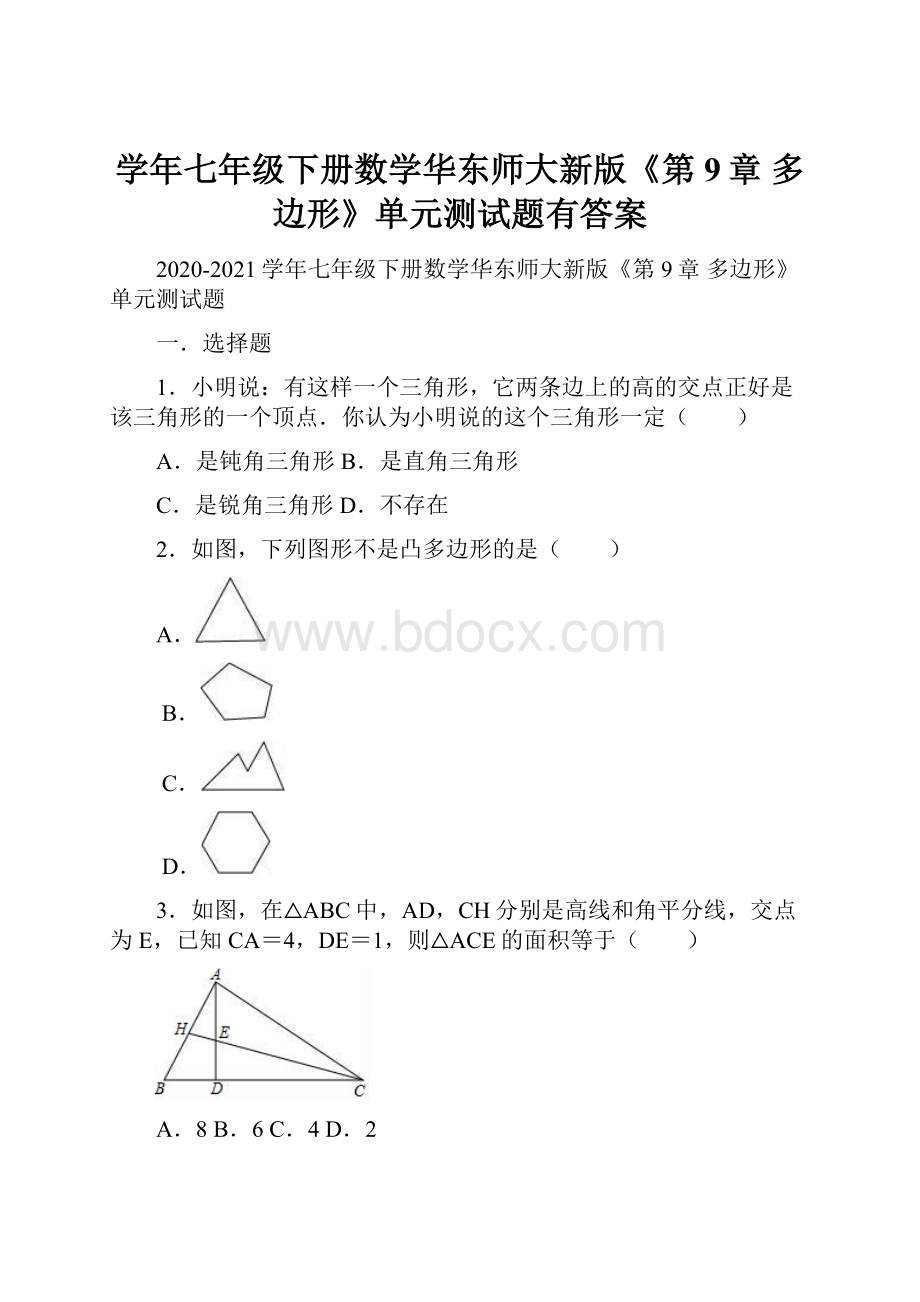
和720°

7．生活中，如图所示的情况，在电线杆上拉两条钢筋，来加固电线杆，这是利用了三角形的（　　）

A．稳定性B．全等性C．灵活性D．对称性

8．以长为3cm，4cm，7cm，11cm的四条线段中的三条线段为边，可以组成三角形的个数是（　　）

A．1B．2C．3D．0

9．若三角形中的一条边是另一条边的2倍，且有一个角为30°

，则这个三角形是（　　）

A．直角三角形B．锐角三角形C．钝角三角形D．以上都不对

10．把一副三角尺按如图所示的方式放置，则两斜边的夹角∠1＝（　　）

A．155°

B．175°

C．165°

D．135°

二．填空题

11．一些大小、形状完全相同的三角形　　密铺地板，正五边形　　密铺地板．（填“能”或“不能”）

12．如图所示的是由相同的小图案无空隙、无重叠地拼接而成，将组成它的小图案画在它右边的方框内　　．

13．已知一个多边形的每一个内角都等于150°

，则此多边形从一个顶点出发的对角线共有　　条，可以将此多边形分成　　个三角形．

14．如图所示，则x＝　　．

15．如果一个三角形三个内角的比是1：

2：

3，那么这个三角形是　　三角形．

16．若三角形的两边长分别是4和3，则第三边长c的取值范围是　　．

17．如图，在△ABC中，AD是BC边上的中线，△ABD的面积为6cm2，则△ABC的面积为　　cm2．

18．如果一个多边形的每个内角都等于150°

，那么它的边数等于　　．

19．折叠式防盗窗利用的是四边形的　　性．

20．在△ABC中，∠ACB＝90°

，CD、CE分别是斜边上的高和中线，若AC＝8，BC＝6，则ED＝　　．

三．解答题

21．如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数．

22．如图，△ABC正好可以放在长方形内，要测出△ABC的面积，现有一把刻度尺，你能做到吗？

说出你是怎样做的．

23．有一块厚度均匀的任意四边形木块，如图所示．如何用作图的方法来确定此木块的重心位置？

请写出作图步骤．

24．如图，在Rt△ABC中，∠C＝90°

，点D，E分别是边AC，BC上的点，点P是一动点．

（1）若点P在线段AB上，如图①，且∠3＝65°

，则∠1与∠2的度数和是多少？

（2）若点P在斜边AB上运动，如图②，探索∠3，∠1，∠2之间的关系，并说明理由．

25．如图，直线a上有5个点，A1，A2，…，A5，图中共有多少个三角形？

26．已知三角形的两边长分别为5cm和2cm，第三边的长是偶数，求第三边的长以及三角形的周长．

27．如图，请复制并剪出若干个纸样，通过拼图解答以下问题．

（1）这种图形能密铺平面吗？

如果你认为能，请用这种图形组成一幅镶嵌图案．

（2）若AB＝4cm，AD＝BC＝1.5cm，由20个这种图形组成的镶嵌图形面积有多大？

参考答案与试题解析

1．解：

∵只有直角三角形三条高相交于直角顶点，

∴这个三角形一定是直角三角形．

故选：

B．

2．解：

选项A、B、D中，画出这个多边形的任意一条边所在的直线，整个多边形都在这条直线的同一侧，所以都是凸多边形，只有C不符合凸多边形的定义，不是凸多边形．

C．

3．解：

过点E作EF⊥AC于F，

∵CE平分∠ACB，ED⊥BC，EF⊥AC，

∴EF＝DE＝1，

∴△ACE的面积＝

×

AC×

EF＝2，

D．

4．解：

根据三角形的内角和定理，三角形的内角至少有两个锐角，

∵∠1＝∠A+∠B，∠2＝∠B+∠C，∠3＝∠A+∠C，

∴∠1、∠2、∠3为三角形的三个外角，

∴△ABC为锐角三角形时∠1、∠2、∠3中锐角有0个，

△ABC为直角三角形时∠1、∠2、∠3中锐角有0个，

△ABC为钝角三角形时∠1、∠2、∠3中锐角有1个，

所以，锐角可能有0个或1个．

5．解：

设多边形有n条边，

则n+

＜20，即n（n﹣1）＜40，

又能被5整除，所以n＝5或6．

6．解：

设这两个正多边形的边数分别为n和2n条，

根据多边形的内角和公式则有两多边形的内角和分别为180（n﹣2）°

和180（2n﹣2）°

，

由于两内角和度数之比为3：

8，

因此

解得：

n＝5，

则180（n﹣2）＝540°

，180（2n﹣2）＝1440°

所以这两多边形的内角和分别为540°

．

7．解：

这是利用了三角形的稳定性．

8．解：

首先进行组合，则有3，7，11；

4，7，3；

3，7，11；

4，7，11，根据三角形的三边关系，没有能组成三角形的．

D

9．解：

如图：

（1）当AB是30°

角所对的边AC的2倍时，△ABC是直角三角形；

（2）当AB是30°

角相邻的边AC的2倍时，△ABC是钝角三角形．

所以三角形的形状不能确定．

10．解：

如图，延长FO交AC于E，

∵∠C＝90°

，∠F＝30°

∴∠AEF＝∠C+∠F＝90°

+30°

＝120°

∵∠A＝45°

∴∠1＝∠A+∠AEF＝45°

+120°

＝165°

11．解：

因为三角形的内角和为180°

所以360°

÷

180°

＝2，

即拼接点处有6个角．

正五边形每个内角是：

﹣360°

5＝108°

，不能整除360°

，不能密铺；

故答案为：

能，不能．

12．解：

作图如下：

13．解：

根据题意得：

360°

（180°

﹣150°

）＝360°

30°

＝12，

那么它的边数是十二．

从它的一个顶点出发的对角线共有12﹣3＝9条，可以把这个多边形分成12﹣2＝10个三角形．

9；

10．

14．解：

∵∠ACD是∠A和∠B的外角，

∴x+（x+10）＝x+70，

解得x＝60．

故答案为60．

15．解：

∵一个三角形三个内角的比是1：

3，

∴这个三角形的最大内角的度数是：

＝90°

∴这个三角形是直角三角形，

直角．

16．解：

根据三角形三边关系，

∴三角形的第三边c满足：

4﹣3＜c＜3+4，即1＜c＜7，

1＜c＜7．

17．解：

∵△ABC中，AD是BC边上的中线，△ABD的面积为6cm2，

∴△ABC的面积＝6×

2＝12cm2．

12．

18．解：

∵多边形的每一个内角都等于150°

∴多边形的每一个外角都等于180°

＝30°

∴边数n＝360°

＝12．

19．解：

折叠式防盗窗利用的是四边形的不稳定性．

20．解：

∵在△ABC中，∠ACB＝90°

，CD、CE分别是斜边上的高和中线，

∴BE＝

，CD⊥AB，

∵AC＝8，BC＝6，∴AB＝

＝10，BE＝5，

∵

•AC•BC＝

•AB•DC，

∴DC＝8×

6÷

10＝4.8．

在△BDC中，BD＝

＝

＝3.6，

∴DE＝BE﹣BD＝5﹣3.6＝1.4．

21．解：

连接CD．

∵在△CDM和△ABM中，∠DMC＝∠BMA，

∴∠A+∠B＝∠BDC+∠ACD，

∴∠A+∠B+∠C+∠D+∠E+∠F＝∠BDC+∠ACD+∠ACF+∠BDE+∠E+∠F＝∠EDC+∠FCD+∠E+∠F＝360°

22．解：

能做到．其方法是：

如图，过点A作AE⊥BC于点E．

则S△ABC＝

BC•AE，S矩形ABCD＝BC•AE，

所以，S△ABC＝

S矩形ABCD．

故只需测出矩形的长和宽即可．

23．解：

作图步骤：

（1）取AB、BC、CD三边的中点G、E、F，连接AE，AF，DE，DG；

（2）分别在AE，AF，DE，DG上取EP＝

AE，FQ＝

AF，ES＝

DE，GR＝

DG；

（3）连接PQ，RS交于O点．

O点即为所求．

24．解：

（1）如图①，连接PC，

∵∠1＝∠PCD+∠CPD，∠2＝∠PCE+∠CPE，

∴∠1+∠2＝∠PCD+∠CPD+∠PCE+∠CPE＝∠3+∠ACB，

∵∠3＝65°

，∠ACB＝90°

∴∠1+∠2＝65°

+90°

＝155°

；

（2）∠1+∠2＝90°

+∠3．

理由：

如图②，连接PC，

∵∠ACB＝90°

∴∠1+∠2＝90°

25．解：

∵直线a上有5个点，

∴直线a上的线段共有：

＝10（条），

即图中共有10个三角形．

26．解：

设第三边为acm，根据三角形的三边关系可得：

5﹣2＜a＜5+2．

即：

3＜a＜7，

由于第三边的长为偶数，

则a可以为4cm或6cm．

∴三角形的周长是2+5+6＝13cm或2+5+4＝11cm．

27．解：

（1）这种图形能密铺平面，

如图所示：

（2）∵由20个这种图形组成的镶嵌图形是有20个4×

1.5的小矩形组成，AB＝4cm，AD＝BC＝1.5cm，

∴镶嵌后图形面积为：

20×

4×

1.5＝120（cm2）．

答：

由20个这种图形组成的镶嵌图形面积为120cm2．