回归分析练习试题和参考答案解析Word文档下载推荐.docx
《回归分析练习试题和参考答案解析Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《回归分析练习试题和参考答案解析Word文档下载推荐.docx(20页珍藏版)》请在冰豆网上搜索。
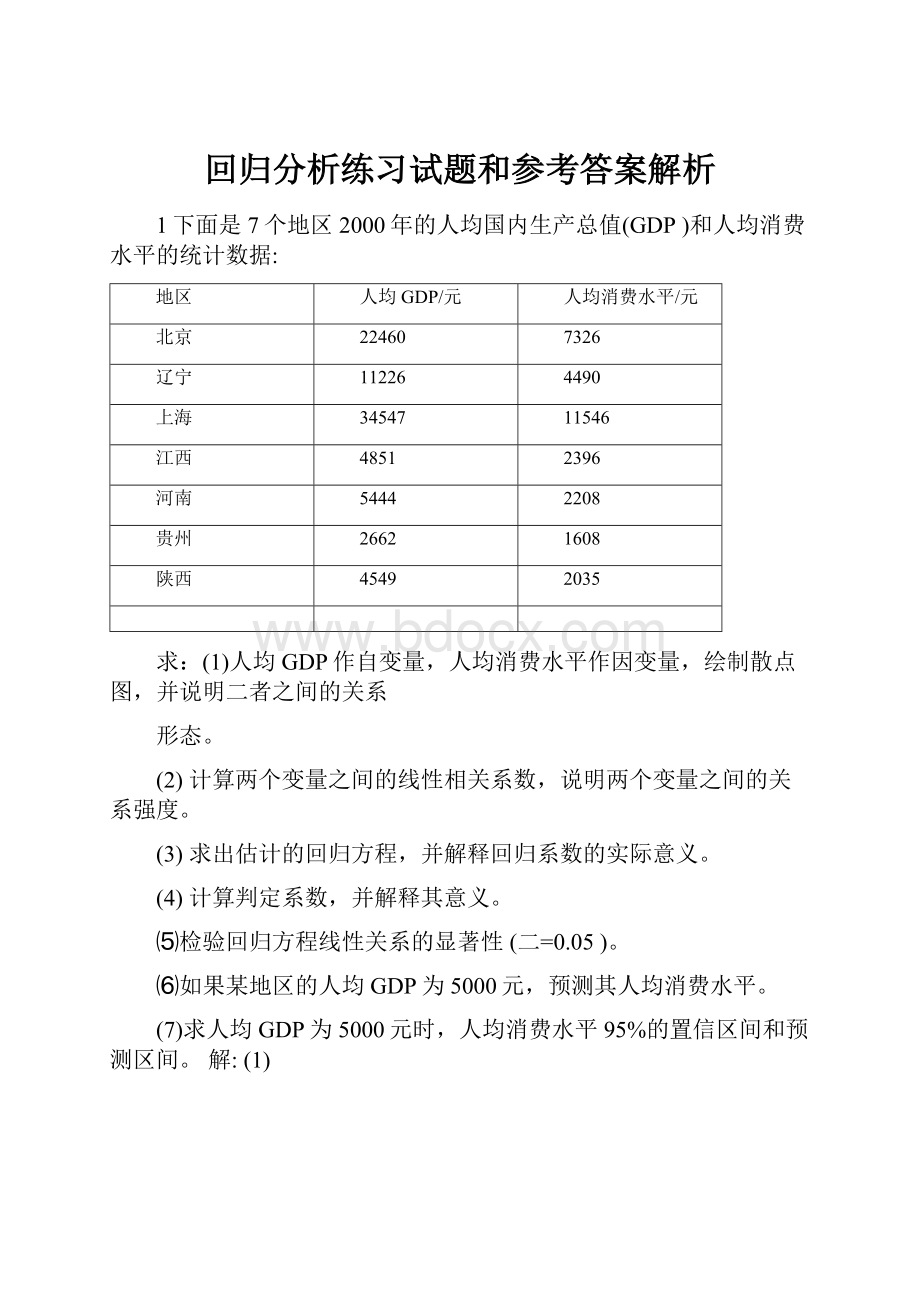
标准系数
t
Sig.
相关性
B
标准误差
试用版
零阶
偏
部分
(常量)
734.693
139.540
5.265
.003
人均GDP
.309
.008
.998
36.492
.000
a.因变量:
人均消费水平
有很强的线性关系。
(3)回归方程:
y=734.693-0.309x
回归系数的含义:
人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
注意:
图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)
标准化系数
显著性
标准误
Beta
0.003
人均GDP(元)
0.309
0.008
0.998
0.000
人均消费水平(元)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
(4)
模型汇总
R
R方
调整R方
标准估计的误
差
a
.996
247.303
a.预测变量:
(常量),人均GDP
人均GDP对人均消费的影响达到99.6%。
模型摘要
R方调整的R方估计的标准差
.998(a)
0.9960.996247.303
a.预测变量:
(常量),人均GDP(元)。
(5)F检验:
Anovab
平方和
df
均方
F
回归
81444968.680
1331.692
.000a
残差
305795.034
5
61159.007
总计
81750763.714
6
a.预测变量:
b.因变量:
回归系数的检验:
t检验
(6)
某地区的人均GDP为5000元,预测其人均消费水平为
y=734.6930.3095000=2278.693(元)。
(7)
人均GDP为5000元时,人均消费水平95%的置信区间为[1990.74915,2565.46399],预测区间为[1580.46315,2975.74999]。
2从n=20的样本中得到的有关回归结果是:
SSR(回归平方和)=60,SSE(误差平方和)
=40。
要检验x与y之间的线性关系是否显著,即检验假设:
h°
:
;
=0。
(1)线性关系检验的统计量F值是多少?
⑵给定显著性水平>-0.05,F:
.是多少?
(3)是拒绝原假设还是不拒绝原假设?
(4)假定x与y之间是负相关,计算相关系数r。
(5)检验x与y之间的线性关系是否显著?
解:
(1)SSR的自由度为k=1;
SSE的自由度为n-k-1=18;
SSR60
因此:
F=k=丄=27
SSE40
n_k-118
(2)F:
"
8=F0.051,18=4.41
(3)拒绝原假设,线性关系显著。
/、/SSRj
(4)r=,=、_0.6=0.7746,由于是负相关,因此r=-0.7746
SSRSSE
(5)从F检验看线性关系显著。
3随机抽取7家超市,得到其广告费支出和销售额数据如下:
超市
广告费支出/万兀
销售额/万元
A
l
19
2
32
C
4
44
D
40
E
10
52
14
53
G
20
54
(1)用广告费支出作自变量x,销售额作因变量y,求出估计的回归方程。
(2)检验广告费支出与销售额之间的线性关系是否显著(:
•=0.05)。
(3)绘制关于x的残差图,你觉得关于误差项;
的假定被满足了吗?
(4)你是选用这个模型,还是另寻找一个更好的模型?
解:
(1)
B标准误
广告费支出
(万元)
29.399
1.547
4.807
0.463
0.831
6.116
3.339
0.002
0.021
销售额(万元)
(2)
回归直线的
F检验:
ANOVA(b)
691.723
1691.723
11.147
.021(a)
310.277
562.055
合计1,002.0006
a.预测变量:
(常量),广告费支出
销售额(万元)显著。
回归系数的t检验:
(万元)。
t显著性
6.1160.002
广告费支出(万元)
3.3390.021
显著。
(3)未标准化残差图:
10.00000
5.00000
IauQ—sftKdeZLQradnals^u
0.00000
-5.00000
-10.00000
-15.00000=
15
标准化残差图:
1.00000
auQIS^RdeZLaraanat
-1.00000
-2.00000
I
学生氏标准化残差图:
2.00000
看到残差不全相等。
(4)应考虑其他模型。
可考虑对数曲线模型:
y=bo+biIn(x)=22.471+11.576ln(x)。
4根据下面SPSS输出的回归结果,说明模型中涉及多少个自变量?
多少个观察值?
写出回
归方程,并根据F,Se,R2及调整的R:
的值对模型进行讨论。
0.842407
0.709650
0.630463
109.429596
321946.8018
3
107315.6006
8.961759
0.002724
131723.1982
11
11974.84
453670
657.0534
167.459539
3.923655
0.002378
VAR00002
5.710311
1.791836
3.186849
0.008655
VAR00003
-0.416917
0.322193
-1.293998
0.222174
VAR00004
-3.471481
1.442935
-2.405847
0.034870
自变量3个,观察值15个。
回归方程:
y=657.0534+5.710311X1-0.416917X2-3.471481X3
拟合优度:
判定系数R2=0.70965,调整的Ra=0.630463,说明三个自变量对因变量的影响的比例占到63%。
估计的标准误差Syx=109.429596,说明随即变动程度为109.429596
回归方程的检验:
F检验的P=0.002724,在显著性为5%的情况下,整个回归方程线性关系显著。
'
-1的t检验的P=0.008655,在显著性为5%的情况下,y与X1线性关系显著。
-2的t检验的P=0.222174,在显著性为5%的情况下,y与X2线性关系
不显著。
:
3的t检验的P=0.034870,在显著性为5%的情况下,y与Xa线性关系显
著。
因此,可以考虑采用逐步回归去除X2,从新构建线性回归模型。
5下面是随机抽取的15家大型商场销售的同类产品的有关数据(单位:
元)。
企业编号
销售价格y
购进价格X1
销售费用X2
1238
966
223
1266
894
257
1200
440
387
1193
664
310
1106
791
339
1303
852
283
7
1313
804
302
8
1144
905
214
9
1286
771
304
1084
511
326
1120
505
12
1156
851
235
13
1083
659
276
1263
490
390
1246
696
316
求:
⑴计算y与xi、y与X2之间的相关系数,是否有证据表明销售价格与购进价格、销售价
格与销售费用之间存在线性关系?
(2)根据上述结果,你认为用购进价格和销售费用来预测销售价格是否有用?
(3)求回归方程,并检验模型的线性关系是否显著(0.05)。
(4)解释判定系数R2,所得结论与问题
(2)中是否一致?
⑸计算X1与X2之间的相关系数,所得结果意味着什么?
(6)模型中是否存在多重共线性?
你对模型有何建议?
(1)y与X1的相关系数=0.309,y与x?
之间的相关系数=0.0012。
对相关性进行检验:
销售价格
购进价格
销售费用
Pearson相关性
0.001
显著性(双侧)
0.263
0.997
N
-.853(**)
**.在.01水平(双侧)上显著相关。
可以看到,两个相关系数的P值都比较的,总体上线性关系也不现状,因此没有明显
的线性相关关系。
(2)意义不大。
(3)
回归统计
MultipleR
0.593684
RSquare
0.35246
AdjustedRSquare
0.244537
69.75121
观测值
方差分析
SS
MS
FSignificaneeF
回归分析
31778.1539
15889.08
3.2658420.073722
58382.7794
4865.232
90160.9333
Coeffieient
s
标准误差tStat
P-value
Lower
95%
Upper
下限
95.0%
上限
339.41056
0.29014
375.6018
21.10663
-363.91
1115.114
0.21044672.55571
x1
0.537841
41
0.0252
0.079317
0.996365
0.66770652.182380.04968
x2
1.457194
96
0.002386
2.912001
从检验结果看,整个方程在5%下,不显著;
而回归系数在5%下,均显著,说明回归
方程没有多大意义,并且自变量间存在线性相关关系。
(4)从R2看,调整后的R2=24.4%,说明自变量对因变量影响不大,反映情况基本一致。
(5)方程不显著,而回归系数显著,说明可能存在多重共线性。
(6)存在多重共线性,模型不适宜采用线性模型。
并想通过广告费
6一家电器销售公司的管理人员认为,每月的销售额是广告费用的函数,
用对月销售额作出估计。
下面是近8个月的销售额与广告费用数据:
96
5.0
1.5
90
2.0
95
4.0
92
2.5
3.0
3.3
94
3.5
2.3
4.2
(1)用电视广告费用作自变量,月销售额作因变量,建立估计的回归方程。
(2)用电视广告费用和报纸广告费用作自变量,月销售额作因变量,建立估计的回归方程。
⑶上述⑴和⑵所建立的估计方程,电视广告费用的系数是否相同?
对其回归系数分别进
行解释。
(4)根据问题
(2)所建立的估计方程,在销售收入的总变差中,被估计的回归方程所解释的比例是多少?
⑸根据问题⑵所建立的估计方程,检验回归系数是否显著(「=0.05)。
(1)回归方程为:
0=88.64+1.6x
(2)回归方程为:
y?
=83.23亠2.29x〔T.3x2
(3)不相同,
(1)中表明电视广告费用增加1万元,月销售额增加1.6万元;
(2)中表明,在报纸广告费用不变的情况下,电视广告费用增加1万元,月销售额增加2.29万丿元。
(4)判定系数R2=0.919,调整的R:
=0.8866,比例为88.66%。
(5)回归系数的显著性检验:
Coefficie标准误LowerUpper下限上限
nts差tStatP-value95%95%95.0%95.0%
1.5738652.8824.57E-
lntercept83.230099480879.1843387.2758579.1843387.27585
电视广告费用工:
x10.304067.53180.0006
(万元)2.290184599531.5085613.0718061.5085613.071806
0.320704.05660.0097
报纸广告费用x2(万元)1.300989297610.4765992.1253790.4765992.125379
假设:
H。
-1=0H1:
'
-1工0
t=」=2.29=7.53
S:
0.304
t°
.°
25(5)=2.57,t>
25(5),认为y与X1线性关系显著。
(3)回归系数的显著性检验:
t亠「3
0.32
=4.05
to.025(5)=2.57,t>
to.o25(5),认为y与X2线性关系显著。
7某农场通过试验取得早稻收获量与春季降雨量和春季温度的数据如下:
收获量y(kg/hm)
降雨量X1(mm)
温度X2(C)
2250
25
3450
33
4500
45
6750
105
7200
110
7500
115
16
8250
120
17
(1)试确定早稻收获量对春季降雨量和春季温度的二元线性回归方程。
⑵解释回归系数的实际意义。
(3)根据你的判断,模型中是否存在多重共线性?
0=-0.591亠22.386x〔亠327.672x2
(2)在温度不变的情况下,降雨量每增加1mm,收获量增加22.386kg/hm2,在降雨
量不变的情况下,降雨量每增加1度,收获量增加327.672kg/hm2。
(3)X1与X2的相关系数rx1X2=0.965,存在多重共线性。
根据企业发展战略的要求,有计划地对人力、资源进行合理配置,通过对
企业中员工的招聘、培训、使用、考核、评价、激励、调整等一系列过程,调动员工地积极性,发挥员工地潜能,为企业创造价值,确保企业战略目标的实现。
读书是一种感悟人生的艺术读杜甫的诗使人感悟人生的辛酸,读李白的诗使人领悟官场的腐败,读鲁迅的文章使人认清社会的黑暗,读巴金的文章使人感到未来的希望每一本书都是一个朋友,
教会我们如何去看待人生读书是人生的一门最不缺少的功课,阅读书籍,感悟人生,助我们走好人生的每一步