数独方法及技巧 小图Word文档格式.docx

数独方法及技巧 小图Word文档格式.docx

《数独方法及技巧 小图Word文档格式.docx》由会员分享，可在线阅读，更多相关《数独方法及技巧 小图Word文档格式.docx（39页珍藏版）》请在冰豆网上搜索。

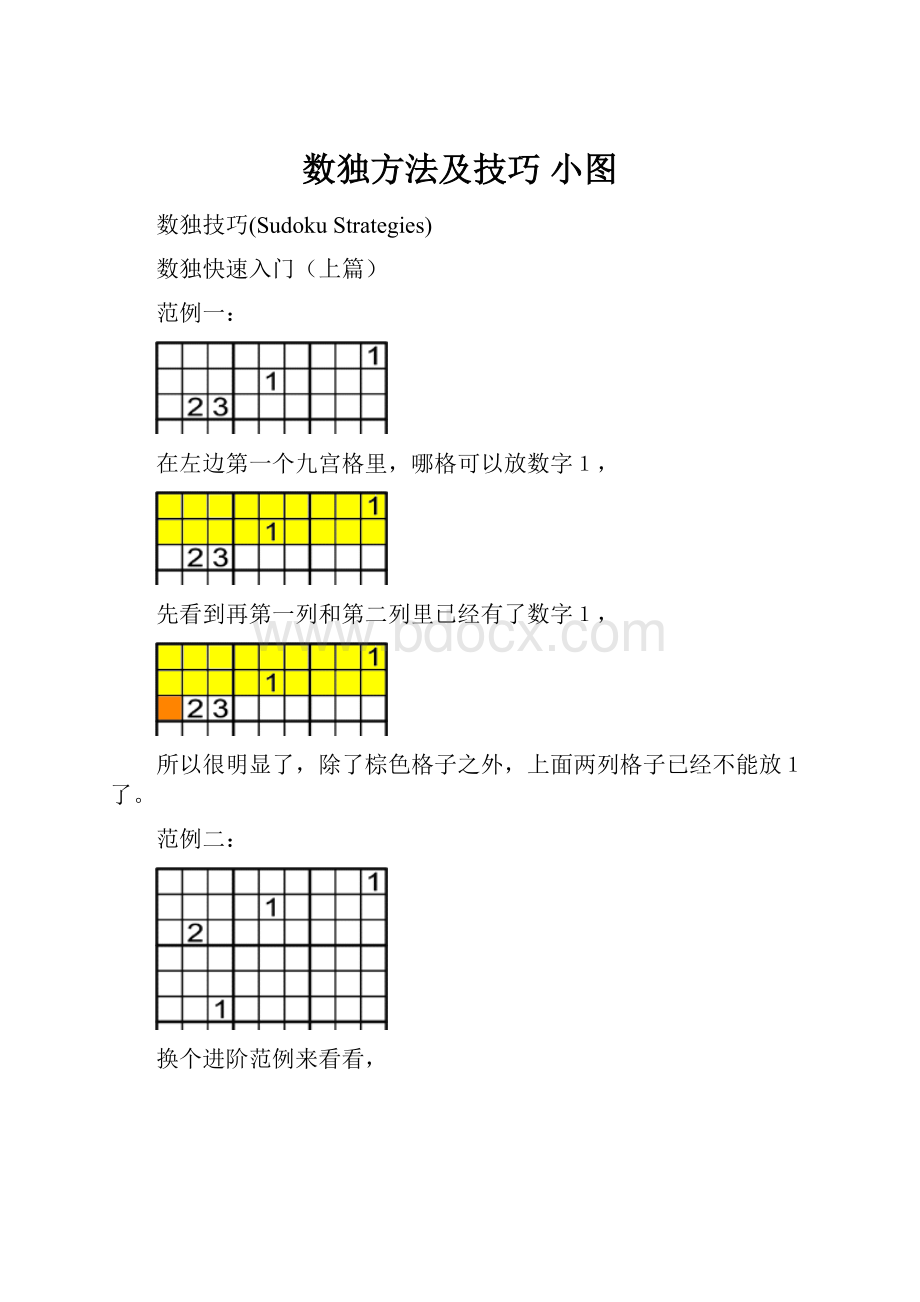
数独快速入门（中篇）

看看这个比上篇难的，想想１能放在哪里呢，

被颜色标示起来的第一列和第一行已经不能放１了，

就左上角的九宫格而言，在红色标示区域似乎是可以摆１的，

但在这里而言，似乎无法决定１放在两格红色区域的哪一格，

所以，可以先看看邻近的九宫格，发现到棕色格子能放１喔，这时候就不用怀疑马上写下１。

看看这个有技术性的，想想１能放在哪里，

看到黄色的第一列已经有１，所以不能再放１了，

就中央的九宫格而言，合理的推论，１一定是在第二列中央红色三格的其中之一了，

既然知道第二列的情况，再考虑黄色区域后，

那么可以先确定右方九宫格的１必然放在这棕色格子。

由上篇的概念再进阶，考虑这上面三个九宫格，看看能否决定１的位置，

黄色标示的第三行已先被排除，

就第一个九宫格而言，１一定在红色区域，

就黄色标示区域来看，已不能再放１了，

这时可以马上先决定右上九宫格里的棕色格子是能放１的啦。

看到这左上方九宫格的第一列，就可以马上知道缺了哪两个数字，

是不是已经看出红色格子不是１就是９了，

但是又看到第二行有１，所以很轻松知道左上棕色格子一定是１，

接下来９就确定在红色格子了。

先看看这第一列，

左上方的九宫格里，第一列绝对有１、８、９，

再考虑到第一行黄色区域，看到有８和９，

这下就可确定１绝对放在左上角的棕色格子。

数独快速入门（下篇）

来看看这个高级进阶例子，可以先把眼光放在第一列和第一行，

看到在黄色区域里都有２和３，所以此黄色区域已经不能再放２和３了，

这时可以考虑到左上九宫格里的红色格子能放２和３，

再看到第一列和第三列的黄色区域，这黄色区域里已经不能放１，

在左上九宫格里，能放１的只有红色与棕色格子，但红色格子将会被２和３所占据，所以能确定棕色格子必然为１。

看看左上方九宫格里，能否由些微线索决定１的位置，

首先，看到第一列后先排除５、６、７，又因左上方九宫格里有２、３、４，再排除这三个数字，这下，在左上方九宫格的第一列，只剩下１、８、９可以填，然后，又看到第一行有８和９，所以，棕色格子必然不会是８和９，那么，就只剩下１可以填入啦！

∙

直观法（DirectEliminationTechniques）

经常在报章杂志上看到的数独谜题，一般就算再难都可以用直观法来解决。

它不需要象那样在每个空白的单元格中用铅笔填上一大堆候选数。

你只要有相对锐利的眼光和一定的逻辑分析能力，就可以准确地把空余的数字逐个填出来。

实际上，直观法就是对数独游戏规则的充分利用。

虽然它并不如那样强大，但通常要想体会解决数独谜题的乐趣，使用直观法却是不二之选。

直观法（DirectEliminationTechniques）具有以下的特点：

轻松上手。

即便是数独新手，在拿到谜题的一刹那，就可以用直观法来解题了。

无需辅助。

在纸上解题时一般只需要一支钢笔就可以。

因为是通过推理和逻辑分析来确定哪个格填哪个数，或是哪个数填在哪个格里，所以基本不需要猜测。

容易掌握。

对于直观法（DirectEliminationTechniques）中应用的各种算法，可以很快掌握并应用于实际中。

相对简单。

比起，它的算法相对比较简单，当然能解决的谜题的复杂度也相对要低。

在直观法（DirectEliminationTechniques）中，常用的算法包括：

1.

2.

3.

4.

5.

6.

这应该算是中最简单的方法了。

基本上只需要看谜题，推理分析一概都用不上，这是因为要使用它所需满足的条件十分明显。

同样，也正是因为它简单，所以只能处理很简单的谜题，或是在处理较复杂谜题的后期才用得上。

我们先来看一个例子：

在上图中，观察行B，可以看到除了[B3]外，其他所有的单元格中都已有了数字，根据数独游戏的规则，即每行，列或区块中不能有重复的数字，则[B3]中能填入的数字只能是行B中所未出现过的，也就是数字3。

所以可以毫不犹豫地在[B3]中填入3。

这就是单元唯一法在行中的应用。

这里的单元（Unit,orgroup），指的是行，列或区块。

所以有三种情况：

当某行有8个单元格中已有数字，或

当某列有8个单元格中已有数字，或

当某区块有8个单元格中已有数字。

无论是哪种情况，我们都可以很快地在该行，列或区块剩余的空格中填入该单元还未出现过的数字。

下面是单元唯一法在列中的应用：

在第7列中，只有[F7]未填入数字，且这一列中数字8还未出现过。

所以[F7]=8。

在区块中也是一样：

在起始于[D7]的区块中，只有[E7]还未填入数字，且这个区块中数字5还未出现过，所以可以马上在[E7]中填入5。

单元唯一法在解题初期应用的几率并不高，而在解题后期，随着越来越多的单元格填上了数字，使得应用这一方法的条件也逐渐得以满足。

单元排除法是中最常用的方法，也是在平常解决数独谜题时使用最频繁的方法。

使用得当的话，甚至可以单独处理中等难度的谜题。

使用单元排除法的目的就是要在某一单元（即行，列或区块）中找到能填入某一数字的唯一位置，换句话说，就是把单元中其他的空白位置都排除掉。

它对应于中的。

那么要如何排除其余的空格呢当然还是不能忘了游戏规则，即行，列或区块中不能有重复的数字。

从另一个角度来理解，就是

如果某行中已经有了某一数字，则该行中的其他位置不可能再出现这一数字。

如果某列中已经有了某一数字，则该列中的其他位置不可能再出现这一数字。

如果某区块中已经有了某一数字，则该区块中的其他位置不可能再出现这一数字。

单纯理解上面的规则还是不足以解题，但是在实践中这些规则却可以交叉使用。

在实际解题过程中，应用最多也最方便的是对区块的单元排除法，我们可以先看下面这个例子：

对于起始于[D1]的区块，其未填数字的空格有6个之多，如果不使用单元排除法，是很难为这一区块填入任何数字的。

这时我们就可以利用行，列及区块的相互关系，即一个单元格既在某一行上，也同时在某一列上以及某一区块中的这种关系来解题。

观察数字9在谜题中的位置，可以看到它出现在[B2]，[A4]，[C7]，[D8]，[I1]和[H9]。

而这些位置中，只有[B2]，[D8]和[I1]与起始于[D1]的区块有关联。

因为[I1]=9，它所在的第1列上的其他单元格中不可能再出现9,而区块中的[D1]和[F1]正好也在第1列上，所以这两个单元格填入9的可能性被排除。

同理，因为[B2]=9，它所在的第2列中的其他单元格不可能再填入9，而区块中的[D2]和[E2]也正好在第2列上，因此，这两个单元格填入9的可能性也被排除掉了。

再看行D，因为[D8]=9，所以该行上的[D1]，[D2]和[D3]也不可能再填入9，而这些单元格正好也在起始于[D1]的区块中。

所以，这个区块中能填入数字9的位置就只剩下了[E3]，这样就通过排除法找到了答案，即[E3]=9。

下面再看一个在行中使用单元排除法的例子：

在谜题中观察数字4和行H，在行H有5个空单元格无法确定数字，但是[C3]位置上的4使得其所在的第3列中的其他单元格上不能再出现4，所以[H3]不能填入4。

[I4]上的4使得其所在的区块中也不能再填入4，它帮助行H排除了两个单元格[H4]和[H6]，而第8列上的[E8]中的数字4使得同样位于这一列上的[H8]也排除了填入4的可能。

这样，行H中能填入4的位置就只剩下[H9]了。

在列中也可以使用单元排除法：

在第7列中，我们试图确定能填入数字1的位置。

在行B中，数字1已经出现在[B2]上，所以[B7]不可能再填入数字1了。

而位于[D8]的数字1也使得[F7]排除了填入数字1的可能，因为它们位于同一区块中。

这样，第7列上就只有[A7]能填入数字1了。

通过上面的示例，可以看到，要对区块使用单元排除法，需要观察与该区块相交的行和列。

要对行使用单元排除法，需要观察与该行相交的区块和列。

要对列使用单元排除法，需要观察与该列相交的区块和行。

在实际解题过程中，行，列和区块之间的关系并不象上面这些图中所示的那么明显，所以需要一定的眼力和细心观察。

一般来说，先看哪个数字在谜题中出现得最多，就从哪个数字开始下手，找到还未填入这个数字的单元（行，列或区块），利用已填入该数字的单元格与单元之间的关系，看能不能排除一些不可能填入该数字的位置，直到剩下唯一的位置。

如果害怕搞不清已经处理过哪些数字的话，可以从数字1开始，从左上角的区块开始一直检查到右下角的区块，看能不能在这些区块中应用单元排除法。

然后测试数字2，以此类推。

单元排除法是应用得最多的，虽然在实践中经常会因为粗心而漏掉很多使用这一方法的机会，但只要勤加练习，就可以运用自如。

区块排除法是中进阶的技法。

虽然它的应用范围不如那样广泛，但用它可能找到用无法找到的解。

有时在遇到困难无法继续时，只要用一次区块排除法，接下去解题就会势如破竹了。

区块排除法实际上是利用区块与行或列之间的关系来实现的，这一点与颇为相似。

然而，它实际上是一种模糊排除法，也就是说，它并不象那样利用谜题中现有的确定数字对行，列或区块进行排除，而是在不确定数字的具体位置的情况下进行排除的。

这句话听起来似乎不好理解，让我们先从一个例子入手，看看区块排除法是怎么应用的。

对于上面这个谜题，用基本的或是都无法再找到解。

这时可以尝试使用区块排除法。

我们先从填入数字最多的区块着手，也就是起始于[G4]的区块，该区块中只有[H6]和[I5]为空，且剩余数字1和2还未填入。

这样，我们可以想办法确定这两个数字的位置。

观察全局，可以看到[D2]=2，根据单元排除法，它所在的第2列上不能再出现数字2，所以[H2]和[I2]将不能填入2，这使得起始于[G1]的区块中数字2可能出现的位置仅剩下[I1]和[I3]，见下图：

虽然我们无法确定2在起始于[G1]的区块中的确定位置，但幸运的是，能填入2的位置正好都在行I上，也就是说，无论2在[I1]还是在[I3]，行I的其他单元格中将不可能再出现数字2，所以可以毫不犹豫地排除在[I5]填入2的可能性，这样，对于起始于[G4]的区块而言，能填入数字2的位置就只剩下[H6]了。

所以[H6]=2。

接下来，当然毫无疑问，利用，在[I5]填入数字1。

先小结一下上面的求解方法：

解题时，实际上是在对目标区块（主区块）有影响的区块（辅助区块）中应用单元，使辅助区块满足某些条件并能参与对主区块的数字排除。

实际应用中，可能出现下面四种情况：

当某数字在某个区块中可填入的位置正好都在同一行上，因为该区块中必须要有该数字，所以这一行中不在该区块内的单元格上将不能再出现该数字。

当某数字在某个区块中可填入的位置正好都在同一列上，因为该区块中必须要有该数字，所以这一列中不在该区块内的单元格上将不能再出现该数字。

当某数字在某行中可填入的位置正好都在同一区块上，因为该行中必须要有该数字，所以该区块中不在该行内的单元格上将不能再出现该数字。

当某数字在某列中可填入的位置正好都在同一区块上，因为该列中必须要有该数字，所以该区块中不在该列内的单元格上将不能再出现该数字。

其中，两种情况相对常见，也比较容易判断。

上面的示例就是情况。

下面我们会看到情况的例子：

虽然在起始于[A7]的区块中，未填入数字的空单元格多达4个，但我们还是可以轻松地确定数字5的位置。

这是因为在起始于[G7]的区块中，我们欣喜地发现数字5可能出现的位置正好都在第8列上，这时5的确切位置已经不重要了，因为它已经满足了上面介绍的第2种情况的条件，因此可以参与对起始于[A7]的区块进行数字排除了。

在它的影响下，[A8]和[B8]中填入数字5的可能性已经不存在，因为它们都在第8列上。

这样，在起始于[A7]的区块中，数字5能填入的位置只剩下[A9]和[C9]了。

这时，我们再利用单元排除法，通过[A4]位置上的数字5再消除其所在行A上的[A9]，最终得到能填入5的唯一位置[C9]。

下面看几个比较少见的例子

在行C上，数字3的位置可以通过下面的方法来确定：

先看行B，利用单元排除法，通过[H2]和[F3]位置上的3进行列排除，得到行B中能填入3的位置为[B4]和[B5]。

碰巧的是，这两个单元格都在起始于[A4]的区块中，这时已经满足了上述情况的条件。

利用单元排除法的区块排除，则行C上的[C4]和[C5]都不能再填入3；

再加上[F3]的列排除的共同努力，最终确定数字3在行C上的唯一位置就是[C1]。

第种情况的例子如下：

在这个示例中，只是使用单元排除法和单元唯一法到这一步就继续不下去了。

要想求得数字8在第6列的位置，就必须要借助区块排除法。

先看第4列，通过位于[C3]和[I8]的数字8的行排除，使8在第4列可能填入的位置只剩下[D4]和[F4]，而这两个单元格正好都在起始于[D4]的区块中。

因为第4列不能没有数字8，而数字8如果填在区块中的其他位置（如[D6]，[E6]或[F6]）时将迫使[D4]和[F4]上不能再填入8，这样会导致第4列没有数字8。

因此，第6列中的[D6]，[E6]和[F6]能填入数字8的可能性被排除。

这样第6列中就只剩下[B6]能填入8了。

实际解题过程中，还会碰到比较复杂的情况，看下面的谜题：

你能确定数字3在起始于[A1]的区块中的位置吗先看位于[C5]的数字3，它不仅排除了同一行中[C1]和[C3]中填入3的可能性，也同时排除了同一行中[C8]和[C9]填入3的可能性，这使得在起始于[A7]的区块中，能填入3的位置只剩下[B8]和[B9]，见下图：

利用区块排除法，在起始于[A7]的区块中，无论3在[B8]还是[B9]，行B中的其他位置都不能再填入3，所以[B1]，[B2]和[B3]都被排除。

于是，在起始于[A1]的区块中，能填入3的位置仅剩下[A1]和[A2]了。

但至此我们还无法确定3的准确位置，这时我们还要借助于其他的辅助区块来进一步排除。

观察起始于[D1]的区块，利用[D7]位置上的3排除同一行的[D1]，以及用[G3]位置上的3排除同一列的[E3]和[F3]，使区块中可能填入3的位置只余[E2]和[F2]，刚好这两个位置都在第2列中，符合上面介绍的第2种情况，于是可以把[A2]也排除掉。

最后，我们就可以很肯定地在[A1]中填入数字3了。

这个例子同时使用了多个辅助区块同时参与排除。

在实际使用中虽然这种情况并不常见，但却也不少见。

关键在于如何能正确识别并恰当应用区块排除法。

相信通过大量的练习并勤于分析思考，这种方法就可以运用自如，得心应手。

下面是其他的一些例子，可以帮助更好地理解并掌握这种技法：

唯一余数法是中较不常用的方法。

虽然它很容易被理解，所以说明这个方法不需要很大篇辐，然而在实践中，却不易看出能够使用这个方法的条件是否得以满足，从而使这个方法的应用受到限制。

与相比，唯一余数法是确定某个单元格能填什么数的方法，而是确定某个数能填在哪个单元格的方法。

另外，应用的条件十分简单，几乎一目了然。

与相比，唯一余数法相当于。

虽然是中最简单且应用最容易的方法，但在中却正好相反。

先看一个例子：

对于单元格[G9]应该填入什么数字，就算你把前面介绍的所有直观技法都用上，也不得而知。

然而，我们通过观察它所在的行，列和区块，可以发现除了数字2以外，1到9中其他的数字都出现了，其中行G中包含了7，6，9，5，3和8，第9列中包含了数字5，8，7和1，起始于[G7]的单元格中包含了3，8，4，7，5和1。

这样，如果[G9]不填入数字2，就一定会违反游戏“行，列或区块不能出现重复数字”的规则。

所以[G9]中的数字一定是2

总结一下，就是如果某一单元格所在的行，列及区块中共出现了8个不同的数字，那么该单元格可以确定地填入还未出现过的数字。

怎么样，很简单吧，但在实践中却不那么容易识别。

看下面的谜题：

你能看出来对哪个单元格应用唯一余数法吗

还有这个谜题：

答案分别是[E6]=9和[I7]=9。

一般来说，只有在使用基本的排除方法都失效的情况下，才试着使用这个方法来解题。

组合排除法和一样，都是中进阶的技法，但它的应用范围要更小一点。

一般情况下，基本没有机会用到这种方法解题，所以要找到相应的例子也都很困难。

当然，如果你希望优先以这个技法来解题的话，还是能碰到很多能符合使用组合排除法条件的情况。

组合排除法，顾名思义，要考虑到某种组合。

这里的组合既包括区块与区块的组合，也包括单元格与单元格的组合，利用组合的关联与排斥的关系而进行某种排除。

它也是一种模糊排除法，同样是在不确定数字的具体位置的情况下进行排除的。

下面先看一个例子：

对于上面这个谜题，你能确定数字6在起始于[G4]的区块中的位置吗

要想获得正确的答案初看起来有些困难。

因为虽然在[G9]和[H3]已经存在了两个6，但是利用它们只能行排除区块中的[G4]和[H6]两个单元格，还是无法确定6到底是在[I4]还是在[I5]中。

这时候，组合排除法就派上用场了。

现在撇开起始于[G4]的区块，先看它上面的两个区块，即起始于[A4]和[D4]的区块。

这几个区块的共同特点是占有同样的几列，也就是第4列至第6列，因此它们之间的数字会相互直接影响。

对于起始于[A4]的区块，利用[A1]处已有的数字6进行行排除，可以得到这个区块中可能填入6的位置只剩下两个：

[B5]和[C6]。

对于起始于[D4]的区块，利用[E7]处已有的数字6进行行排除，可以得到这个区块中可能填入6的位置也剩下两个：

[F5]和[F6]。

这时，我们仍无法确定6在这两个区块中的确切位置。

但不妨对可能出现的情况作一下分析：

假设在起始于[A4]的区块中，[B5]=6，则同一区块中的[C6]必不为6，而且[B5]还将列排除[F5]，这样在起始于[D4]的区块中，只有[F6]=6。

假设在起始于[A4]的区块中，[C6]=6，则同一区块中的[B5]必不为6，而且[C6]还将列排除[F6]，这样在起始于[D4]的区块中，只有[F5]=6。

简单地说，只有两种可能：

[B5]=6且[F6]=6，或者[C6]=6且[F5]=6。

决不会再出现其他的情况。

但无论是其中哪一种情况，第5列和第6列都会有确定的6出现在这两个区块中，也就是说，第5列和第6列的其他位置不可能再出现数字6。

这样，原本无法肯定的6在起始于[G4]区块中的位置，一下子就变得明确了。

利用起始于[A4]和[D4]的区块对起始于[G4]的区块进行列排除，可以把[I5]排除掉，这样，就只剩下[I4]可以填入6了。

小结一下，组合排除法的要满足的条件如下：

如果在横向并行的两个区块中，某个数字可能填入的位置正好都分别占据相同的两行，则这两行可以被用来对横向并行的另一区块做行排除。

如果在纵向并行的两个区块中，某个数字可能填入的位置正好都分别占据相同的两列，则这两列可以被用来对纵向并行的另一区块做列排除。

让我们再看一个例子：

要想确定数字1在起始于[D4]的单元格中的位置，我们将设法借助于其横向上相邻两个区块的帮助。

利用[I2]的列排除，我们可以把起始于[D1]的区块中的[E2]和[F2]排除掉，这样，这个区块中能填入1的位置剩下[D1]，[D3]和[E1]。

利用[H7]的列排除，可以把起始于[D7]的区块中的[E7]和[F7]排除掉，再利用[A9]的列排除，可以把这个区块中[E9]和[F9]排除掉，这样，这个区块中能填入1的位置只剩下[D8]和[E8]。

虽然在起始于[D1]的区块中，能填入1的位置多达3个，但是它们正好只分布在行D和行E上，而且在起始于[D7]的区块中能填入1的位置所占据的也是这两行。

最终1的位置只可能有三种情况：

[D1]=1且[E8]=1；

或者[D3]=1且[E8]=1；

或者[E1]=1且[D8]=1。

无论是哪种情况，行D和行E都会有确定的1出现在这两个区块中，也就是说，这两行的其他位置不会再出现1。

于是，

借助于这两个区块的行排除，我们可以把起始于[D4]的区块中的[D4]和[D6]排除掉，再利用[G4]位置的列排除，最终确定1的位置在[F6]。

下面是其他一些使用组合排除法的例子：

在实践中，组合排除法的实际应用机会不如多。

但是，掌握这一技法无疑可以大大提高求解谜题的灵活性，从而增加解题的乐趣。

矩形排除法虽然浅显易懂，但一般在实际解题的时候应用得却比较少。

这是因为即使谜题中存在满足使用这一方法的情况，也很难直接看出来。

然而，相对而言，在解题过程中倒是能有更多的机会用上矩形排除法。

对于这个谜题，如果不用矩形排除法是无法继续下去的。

我们将通过讲解这种技法，从而找到数字8在起始于[G1]的区块中的位置。

乍看之下，好象一筹莫展。

因为[B2]和[E3]上的8只能列排除左下角这个区块中的[G2]，[H2]，[G3]和[I3]这4个单元格，这时仍剩下两个单元格[G1]和[H1]无法确定。

让我们先来留意一下第6列，这一列中暂时没有8，那么8可能会填入哪几个单元格中呢首先，[B2]中的8行排除了[B6]，而[E3]和[F4]中的8又分别行排除了[E6]和[F6]。

这样，能填入8的位置就只剩下[C6]和[I6]了。

见下图：

同样，对于第9列，由于[F4]的行排除，[F9]不可能填8，所以这一列能填入8的位置也就只剩下[C9]和[I9]了。

凑巧的是，这两列中能填入8的位置都在同样的两行上，即行C和行I。

这时就为我们应用矩形排除法创造了前提条件。

如果第6列中[C6]=8，那么[I6]和[C9]一定不能是8。

而第9列这时就只剩下[I9]能填入8了；

又或者如果第6列中[I6]=8，那么[C6]和[I9]一定不能是8，而第9列就只剩下[C9]能填入8了。

不可能再有第3种情况。

所以，要么[C6]=8且[I9]=8，要么[I6]=8且[C9]=8。

但无论是哪种情况，不难发现，行C和行I都已填入了8，所以这两行的其他位置不可能再填入8。

我们正好可以利用这一点来进行排除。

观察起始于[G1]的区块，我们已经知道现在只剩下[G1]和[I1]两个单元格无法确定了，通过上面的分析，利用矩形排除法排除位于行I上的[I1]，就可以确定数字8一定在[G1]上。

总结一下，使用矩形排除法的条件如下：

如果一个数字在某两行