不规则图形面积计算Word文件下载.docx

不规则图形面积计算Word文件下载.docx

《不规则图形面积计算Word文件下载.docx》由会员分享，可在线阅读，更多相关《不规则图形面积计算Word文件下载.docx（6页珍藏版）》请在冰豆网上搜索。

1.5h

学习目标

掌握不规则图形面积公式

授课时间

重点难点

面积公式的应用

学习过程

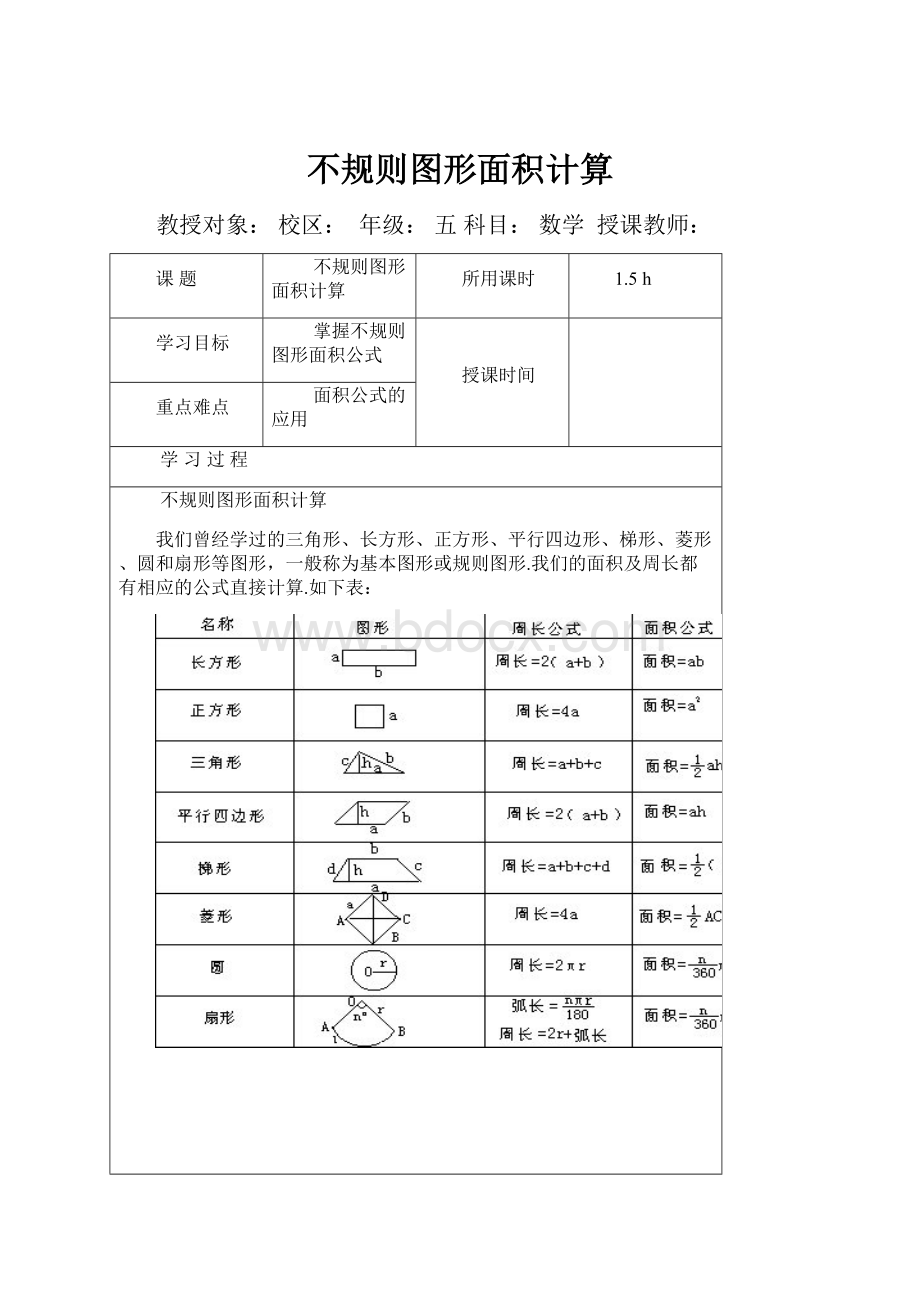
我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：

实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？

我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

一、例题与方法指导

例1、如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

思路导航：

阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2、如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.

∵△ABE、△ADF与四边形AECF的面积彼此相等，

∴四边形AECF的面积与△ABE、△ADF的面积都等于正方形ABCD的

。

在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，

∴△ECF的面积为2×

2÷

2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3、两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

在等腰直角三角形ABC中

∵AB=10

∵EF=BF=AB-AF=10-6=4，

∴阴影部分面积=S△ABG-S△BEF=25-8=17（平方厘米）。

例4、如右图，A为△CDE的DE边上中点，BC=CD，若△ABC（阴影部分）面积为5平方厘米.

求△ABD及△ACE的面积.

取BD中点F，连结AF.因为△ADF、△ABF和△ABC等底、等高，

所以它们的面积相等，都等于5平方厘米.

　∴△ACD的面积等于15平方厘米，△ABD的面积等于10平方厘米。

例5、一个正方形，将它的一边截去15厘米，另一边截去10厘米，剩下的长方形比原

来正方形的面积减少1725厘米2，求剩下的长方形的面积。

分析与解：

根据已知条件画出下页图，其中甲、乙、丙为截去的部分。

由左上图知，丙是长15厘米、宽10厘米的矩形，面积为15×

10=150（厘米2）。

因为甲、丙形成的矩形的长等于原正方形的边长，乙、丙形成的矩形的长也等于

原正方形的边长，所以可将两者拼成右上图的矩形。

右上图矩形的宽等于10+15=25

（厘米），长等于原正方形的边长，面积等于（甲+丙）+（乙+丙）

=（甲+乙+丙）+丙

=1725+150=1875（厘米2）。

所以原正方形的的边长等于1875÷

25=75（厘米）。

剩下的长方形的面积等于75

×

75-1725=3900（厘米2）。

六、有红、黄、绿三块同样大小的正方形纸片，放在一个正方形盒的底部，它们之间

互相叠合（见右图）。

已知露在外面的部分中，红色面积是20，黄色面积是14，绿

色面积是10，求正方形盒子底部的面积。

把黄色正方形纸片向左移动并靠紧盒子的左边。

由于三个正方形纸片

面积相等，所以原题图可以转化成下页右上图。

此时露出的黄、绿两部分的面积相等，

都等于

（14+10）÷

2=12

因为绿：

红=A∶黄，所以绿×

黄=红×

A，

A=绿×

黄÷

红

=12×

12÷

20=7.2。

正方形盒子底部的面积是红+黄+绿+A=20+12+12+7.2=51.2。

　又由于△ACE与△ACD等底、

等高，所以△ACE的面积是15平方厘米。

二、巩固训练

1.如右图，在正方形ABCD中，三角形ABE的面积是8平方厘米，它是三角形DEC的面积的0.8倍，求正方形ABCD的面积。

2.如右图，正方形ABCD的边长是4厘米，CG=3厘米，矩形DEFG的长DG为5厘米，求它的宽DE等于多少厘米

3.如右图，梯形ABCD的面积是45平方米，高6米，△AED的面积是5平方米，BC=10米，求阴影部分面积.

4.如右图，四边形ABCD和DEFG都是平行四边形，证明它们的面积相等.

3、练习

1、如左下图所示，平行四边形ABCD的周长是75厘米，以BC为底的高是14厘米，以CD为底的高是16厘米。

求平行四边形ABCD的面积。

2、如下图，在三角形ABC中，BD=DF=FC，BE=EA。

若三角形EDF的面积是1，则三角形ABC的面积是多少？

3、如下图所示，四边形ABCD的面积是1，将BA，CB，DC，AD分别延长一倍到E，F，G，H，连结E，F，G，H。

问：

得到的新四边形EFGH的面积是多少？

教学部意见：

教学校长：

年月日

WelcomeTo

Download!

!

欢迎您的下载，资料仅供参考！