初二轴对称经典习题附答案Word文档格式.docx

初二轴对称经典习题附答案Word文档格式.docx

《初二轴对称经典习题附答案Word文档格式.docx》由会员分享，可在线阅读，更多相关《初二轴对称经典习题附答案Word文档格式.docx（21页珍藏版）》请在冰豆网上搜索。

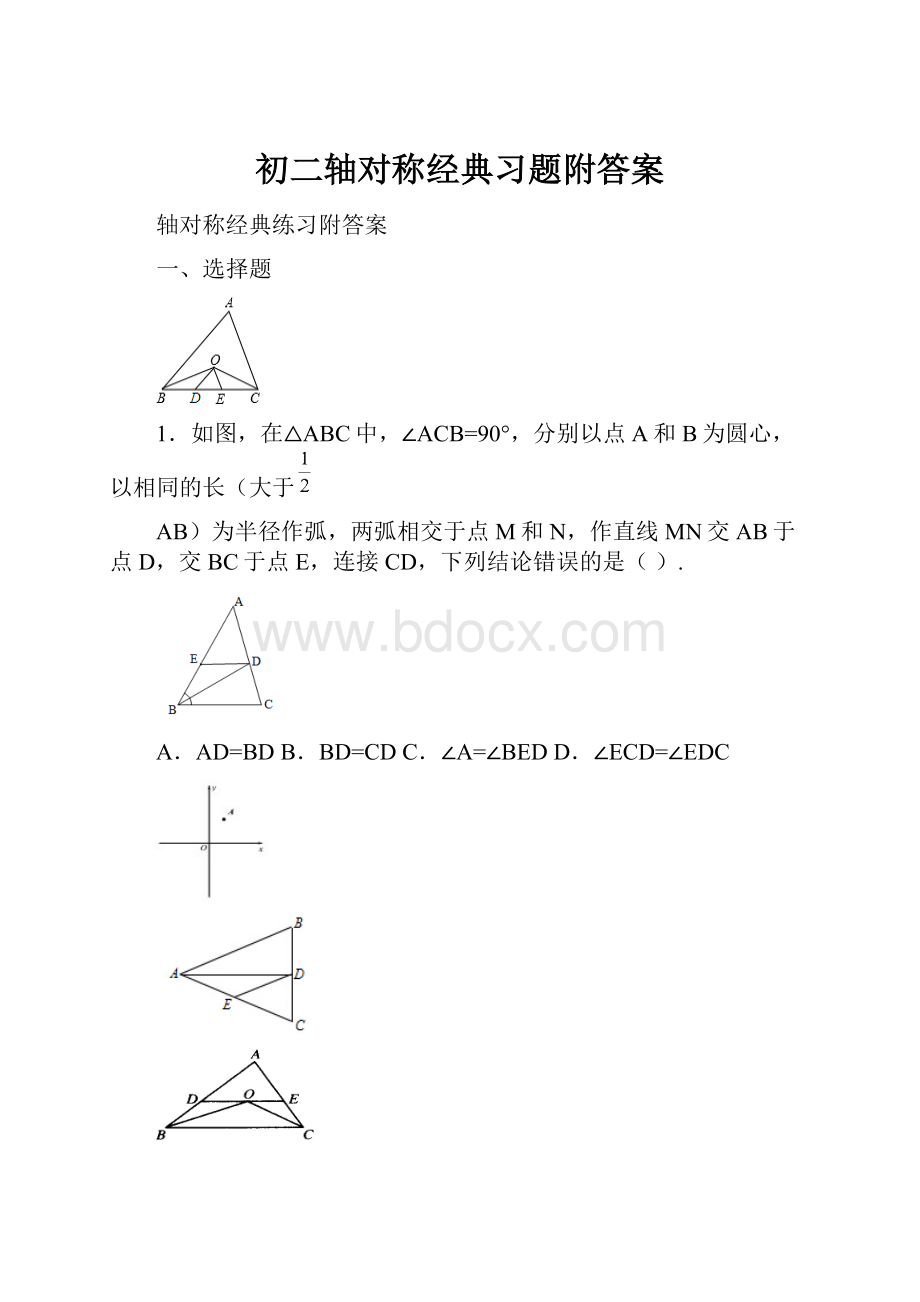
，D为△ABC内一点，∠BAD＝15°

，AD＝AC，CE⊥AD于E，且CE＝5.

（1）求BC的长；

（2）求证：

BD＝CD.

24．如图，△ABC中，AC=BC，∠ACB=120°

，点D在AB边上运动（D不与A、B重合），连结CD．作∠CDE=30°

，DE交AC于点E．

（1）当DE∥BC时，△ACD的形状按角分类是直角三角形；

（2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？

若可以，请求出∠AED的度数；

若不可以，请说明理由．

25．如图，在△ABC中，AC=BC，∠C=90°

，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：

DE=DF．

参考答案

1．D.

【解析】

试题分析：

∵MN为AB的垂直平分线，∴AD=BD，∠BDE=90°

；

∵∠ACB=90°

，∴CD=BD；

∵∠A+∠B=∠B+∠BED=90°

，∴∠A=∠BED；

∵∠A≠60°

，AC≠AD，∴EC≠ED，∴∠ECD≠∠EDC．

故选：

D．

考点：

作图—基本作图；

线段垂直平分线的性质；

直角三角形斜边上的中线．

2．C

根据AB=AC，AD平分∠BAC，则点D为BC的中点，AD⊥BC，则CD=4，根据直角三角形斜边上的中线的性质可得：

DE=AE，则△CDE的周长=DE+EC+CD=AE+EC+CD=AC+CD=12+4=16.

（1）、等腰三角形的性质；

（2）、直角三角形的性质

3．C

根据等腰三角形的性质可得：

点M的坐标为（0,2）；

（0，-2）；

（2,0）；

（-2,0）；

（0,2

）；

（0，

）共6个点.

等腰三角形的性质

4．A

根据角平分线的性质可得：

∠OBD=∠OBC，∠OCB=∠OCE，根据平行线的性质可得：

∠OBD=∠DOB，∠OCE=∠COE，则BD=DO，CE=OE，即DE=DO+OE=BD+CE=5.

5．C．

∵BD平分∠ABC，∴∠ABD=∠CBD，∵ED∥BC，∴∠CBD=∠BDE，∴∠ABD=∠BDE，∴BE=DE，△AED的周长=AE+DE+AD=AE+BE+AD=AB+AD，∵AB=3，AD=1，∴△AED的周长=3+1=4．故选C．

等腰三角形的判定与性质；

平行线的性质．

6．2

或2

当∠APB=90°

时（如图1），

∵AO=BO，

∴PO=BO，

∵∠AOC=60°

，

∴∠BOP=60°

∴△BOP为等边三角形，

∵AB=BC=4，

∴AP=ABsin60°

=4×

=2

当∠ABP=90°

时（如图2），

∵∠AOC=∠BOP=60°

∴∠BPO=30°

∴BP=

在直角三角形ABP中，

AP=

情况二：

如图3，∵AO=BO，∠APB=90°

∴PO=AO，

∴△AOP为等边三角形，

∴AP=AO=2，

故答案为：

2

或2．

勾股定理．

7．15°

或30°

或60°

或75°

或150°

根据点P在等边△ABC外部，且与等边△ABC三个顶点中的任意两个顶点形成的三角形都是等腰三角形，找出点P的位置，求得∠APC的度数即可．根据点P在等边△ABC外部，且与等边△ABC三个顶点中的任意两个顶点形成的三角形都是等腰三角形，作出如下图形：

由图可得：

∠AP1C=15°

，∠AP2C=30°

，∠AP3C=60°

，∠AP4C=75°

，∠AP5C=150°

（1）、等边三角形的性质；

（2）、等腰三角形的性质

8．105°

根据AC=AD可得：

∠CDA=∠A=50°

，则∠ACD=80°

，根据中垂线的性质以及外角的性质可得：

∠B=∠BCD=25°

，则∠ACB=80+25=105°

.

9．5

根据等腰三角形的判定定理可得：

△ADE、△BDE、△BDC、△ABD和△ABC为等腰三角形.

等腰三角形的判定

10．42°

根据AB=AC，∠A=32°

，则∠ABC=∠C=74°

，根据中垂线的性质可得：

∠ABD=32°

，则∠CBD=∠ABC－∠ABD=74°

－32°

=42°

中垂线的性质

11．15°

设∠F=x°

，根据等腰三角形和外角的性质可得：

∠DEC=2x°

，∠ACB=4x°

，根据等边三角形的性质可得：

4x=60°

，则x=15°

，即∠F=15°

12．70°

或110°

本题需要分两种情况来进行讨论，分别画出图形得出答案.两种情况即为锐角三角形和钝角三角形.

（2）、分类讨论思想

13．5

过点P作PE⊥MN，根据等腰三角形底边上的三线合一定理可得ME=

MN=1，根据∠O=60°

可得∠OPE=30°

，则OE=

OP=6，则OM=OE－ME=6－1=5.

勾股定理.

14．10

根据角平分线的性质以及平行线的性质，把△ODE三条边转移到同一条线段BC上，即可解答．

解：

∵OC、OB分别是∠ACB、∠ABC的角平分线，

∴∠5=∠6，∠1=∠2，

∵OD∥AB，OE∥AC，

∴∠4=∠6，∠1=∠3．

∴∠4=∠5，∠2=∠3，

即OD=BD，OE=CE．

∴△ODE的周长=OD+DE+OE=BD+DE+CE=BC=10cm．

10．

【点评】此题比较简单，利用的是角平分线的定义，平行线及等腰三角形的性质．

15．

要求EM+CM的最小值，需考虑通过作辅助线转化EM，CM的值，从而找出其最小值求解．

连接BE，与AD交于点M．则BE就是EM+CM的最小值．

取CE中点F，连接DF．

∵等边△ABC的边长为6，AE=2，

∴CE=AC﹣AE=6﹣2=4，

∴CF=EF=AE=2，

又∵AD是BC边上的中线，

∴DF是△BCE的中位线，

∴BE=2DF，BE∥DF，

又∵E为AF的中点，

∴M为AD的中点，

∴ME是△ADF的中位线，

∴DF=2ME，

∴BE=2DF=4ME，

∴BM=BE﹣ME=4ME﹣ME=3ME，

∴BE=

BM．

在直角△BDM中，BD=

BC=3，DM=

AD=

∴BM=

=

∵EM+CM=BE

∴EM+CM的最小值为

点评：

考查等边三角形的性质和轴对称及勾股定理等知识的综合应用．

16．

＜x＜5．

试题解析：

依题意得：

10-2x-x＜x＜10-2x+x，

解得

1.等腰三角形的性质；

2.解一元一次不等式组；

3.三角形三边关系．

17．2

作PE⊥OA于E，根据角平分线的性质可得PE=PD，根据平行线的性质可得∠ACP=∠AOB=30°

，由直角三角形中30°

的角所对的直角边等于斜边的一半，可求得PE，即可求得PD．

作PE⊥OA于E，∵∠AOP=∠BOP，PD⊥OB，PE⊥OA，∴PE=PD（角平分线上的点到角两边的距离相等），

∵∠BOP=∠AOP=15°

，∴∠AOB=30°

，∵PC∥OB，∴∠ACP=∠AOB=30°

∴在Rt△PCE中，PE=

PC=

×

4=2（在直角三角形中，30°

角所对的直角边等于斜边的一半），

∴PD=PE=2，

（1）角平分线的性质；

（2）含30度角的直角三角形．

18．36

连接BD，

∵AB=AC，∠A=36°

∴∠C=∠ABC=72°

∵BE=BD=BC，

∴∠BDC=72°

∴∠DBC=36°

∴∠EBD=36°

∴∠EDB=72°

∴∠ADE=180°

﹣72°

=36°

36

19．

如图，作EF⊥AB垂足为F，连接CF．

∴∠ABC=60°

∵△EBD是等边三角形，

∴BE=BD，∠EBD=60°

∴∠EBD=∠ABC，

∴∠EBF=∠DBC，

又∵EB=BD，

∴△EBF≌△DBC，

∴BF=BC，EF=CD，

∵∠FBC=60°

∴△BFC是等边三角形，

∴CF=BF=BC，

∵BC=

AB，

∴BF=

∴AF=FB，

∴点E在AB的垂直平分线上，

∴在点D从点A移动至点C的过程中，点E移动的路线和点D运动的路线相等，

∴在点D从点A移动至点C的过程中，点E移动的路线为

等边三角形的性质；

含30度角的直角三角形．

20．10．

因为2+2＜4，所以等腰三角形的腰的长度是4，底边长2，周长：

4+4+2=10，答：

它的周长是10，故答案为：

等腰三角形的性质；

三角形三边关系．

21．55.

∵∠AFD=145°

，∴∠CFD=35°

又∵FD⊥BC于D，DE⊥AB于E

∴∠C=180°

-（∠CFD+∠FDC）=55°

∵AB=AC

∴∠B=∠C=55°

，∴∠A=70°

根据四边形内角和为360°

可得：

∠EDF=360°

-（∠AED+∠AFD+∠A）=55°

∴∠EDF为55°

2.三角形内角和定理．

22．

（1）、10；

（2）、证明过程见解析

（1）、根据等腰直角三角形的性质得出∠BAC=45°

，从而得出∠CAD=30°

，根据垂直得出AC=BC=10；

（2）、过D作DF⊥BC于F，然后证明Rt△DCE和Rt△DCF全等，从而得出CF=CE=5，根据BC=10得出BF=FC，从而得出答案.

（1）、在△ABC中，∵AC＝BC，∠ACB＝90°

，∴∠BAC＝45°

∵∠BAD＝15°

，∴∠CAD＝30°

．∵CE⊥AD，CE＝5，∴AC＝10．∴BC＝10．

（2）、过D作DF⊥BC于F.在△ADC中，∠CAD＝30°

，AD＝AC，∴∠ACD＝75°

∵∠ACB＝90°

，∴∠FCD＝15°

．在△ACE中，∠CAE＝30°

，CE⊥AD，∴∠ACE＝60°

∴∠ECD＝∠ACD－∠ACE＝15°

．∴∠ECD＝∠FCD.∴DF＝DE.

在Rt△DCE与Rt△DCF中，

∴Rt△DCE≌Rt△DCF.

∴CF＝CE＝5．∵BC＝10，∴BF＝FC．∵DF⊥BC，∴BD＝CD．

（1）、三角形内角和定理；

（2）、三角形全等的判定与性质

23．

（1）、证明见解析；

（2）、直角三角形、理由见解析；

（3）、不能，理由见解析；

（4）、α=110°

或125°

或140°

（1）、根据△BOC≌△ADC得到OC=DC，结合∠OCD=60°

，从而得出等边三角形；

（2）、根据△BOC≌△ADC，∠α=150°

得到∠ADC=∠BOC=150°

，根据等边三角形得到∠ODC=60°

，从而得出∠ADO=90°

，从而得到三角形的形状；

（3）、由△BOC≌△ADC，得∠ADC=∠BOC=∠α，当△AOD为等边三角形时，则∠ADO=60°

，结合∠ODC=60°

得出∠ADC=120°

，又根据∠AOD=∠DOC=60°

得出∠AOC=120°

，从而求出∠AOC+∠AOB+∠BOC≠360°

，从而得到答案；

（4）、根据△OCD是等边三角形得到∠COD=∠ODC=60°

，根据三角形的性质得出∠ADC=∠BOC=α，∠AOD=190°

－α，∠OAD=50°

，然后分三种情况分别求出α的大小.

（1）、∵△BOC≌△ADC，∴OC=DC．∵∠OCD=60°

，∴△OCD是等边三角形．

（2）、△AOD是Rt△．理由如下：

∵△OCD是等边三角形，∴∠ODC=60°

，∵△BOC≌△ADC，∠α=150°

，∴∠ADC=∠BOC=∠α=150°

∴∠ADO=∠ADC-∠ODC=150°

-60°

=90°

，∴△AOD是Rt△．

（3）、不能理由：

由△BOC≌△ADC，得∠ADC=∠BOC=∠α.

若△AOD为等边三角形，则∠ADO=60°

，又∠ODC=60°

，∴∠ADC=∠α=120°

又∠AOD=∠DOC=60°

，∴∠AOC=120°

，又∵∠AOB=110°

∴∠AOC+∠AOB+∠BOC=120°

+120°

+110°

=350°

<

360°

．所以△AOD不可能为等边三角形.

（4）、∵△OCD是等边三角形，∴∠COD=∠ODC=60°

．∵∠AOB=110°

，∠ADC=∠BOC=α，

∴∠AOD=360°

-∠AOB-∠BOC-∠COD=360°

-110°

-α-60°

=190°

-α，∠ADO=∠ADC-∠ODC=α-60°

∴∠OAD=180°

-∠AOD-∠ADO=180°

-（190°

-α）-（α-60°

）=50°

①当∠AOD=∠ADO时，190°

-α=α-60°

，∴α=125°

②当∠AOD=∠OAD时，190°

-α=50°

，∴α=140°

③当∠ADO=∠OAD时，α-60°

=50°

，∴α=110°

综上所述：

当α=110°

时，△AOD是等腰三角形．

（1）、三角形全等；

（2）、分类讨论思想.

24．

（1）、直角三角形；

（2）、△ECD可以是等腰三角形，∠AED=60°

或105°

（1）、由DE∥BC得到∠BCD=∠CDE=30°

，再由∠ACB=120°

，得到∠ACD=120°

﹣30°

，则△ACD是直角三角形；

（2）、分类讨论：

当∠CDE=∠ECD时，EC=DE；

当∠ECD=∠CED时，CD=DE；

当∠CED=∠CDE时，EC=CD；

然后利用等腰三角形的性质和三角形的内角和定理进行计算．

（1）、∵△ABC中，AC=BC，∴∠A=∠B=

=30°

∵DE∥BC，∴∠ADE=∠B=30°

，又∵∠CDE=30°

，∴∠ADC=∠ADE+∠CDE=30°

+30°

=60°

∴∠ACD=180°

﹣∠A﹣∠ADC=180°

﹣60°

，∴△ACD是直角三角形；

（2）、△ECD可以是等腰三角形．理由如下：

①当∠CDE=∠ECD时，EC=DE，∴∠ECD=∠CDE=30°

，∵∠AED=∠ECD+∠CDE，∴∠AED=60°

②当∠ECD=∠CED时，CD=DE，∵∠ECD+∠CED+∠CDE=180°

∴∠CED=

=75°

，∴∠AED=180°

﹣∠CED=105°

③当∠CED=∠CDE时，EC=CD，∠ACD=180°

﹣∠CED﹣∠CDE=180°

=120°

∵∠ACB=120°

，∴此时，点D与点B重合，不合题意．

综上，△ECD可以是等腰三角形，此时∠AED的度数为60°

（2）、分类讨论思想的运用；

（3）、等腰三角形的判定与性质．

25．证明过程见解析．

首先可判断△ABC是等腰直角三角形，连接CD，根据全等三角形的判定易得到△ADE≌△CDF，继而可得出结论．

如图，连接CD．∵BC=AC，∠BCA=90°

∴△ABC是等腰直角三角形∵D为AB中点

∴BD=CD=AD，CD平分∠BCA，CD⊥AB∵∠A+∠ACD=∠ACD+∠FCD=90°

∴∠A=∠FCD

∵∠CDF+∠CDE=90°

∠CDE+∠ADE=90°

∴∠ADE=∠CDF，在△ADE和△CFD中，

∵∠A=∠FCD，AD=CD，∠ADE=∠CDF∴△ADE≌△CFD（ASA）∴DE=DF．

（1）、全等三角形的判定与性质；

（2）、等腰直角三角形．

26．∠BAD=20°

∠EDC=30°

根据DE⊥AC，AD=AE，∠DAE=80°

得出∠ADE=∠E=50°

，∠DAF=∠EAF=40°

，根据等边三角形的性质得出∠BAD的度数，根据三角形内角和定理得出∠EDC的度数.

当DE⊥AC时，∵AD=AE，∠DAE=80°

∴∠ADE=∠E=50°

∠DAF=∠EAF=40°

∵△ABC是等边三角形∴∠BAC=60°

∴∠BAD=60°

﹣40°

=20°

∵∠B+∠BAD=∠ADE+∠EDC∴60°

+20°

+∠EDC∴∠EDC=30°

三角形内角和定理