最新高考数学总复习讲+练+测 专题3Word格式文档下载.docx

最新高考数学总复习讲+练+测 专题3Word格式文档下载.docx

《最新高考数学总复习讲+练+测 专题3Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《最新高考数学总复习讲+练+测 专题3Word格式文档下载.docx（12页珍藏版）》请在冰豆网上搜索。

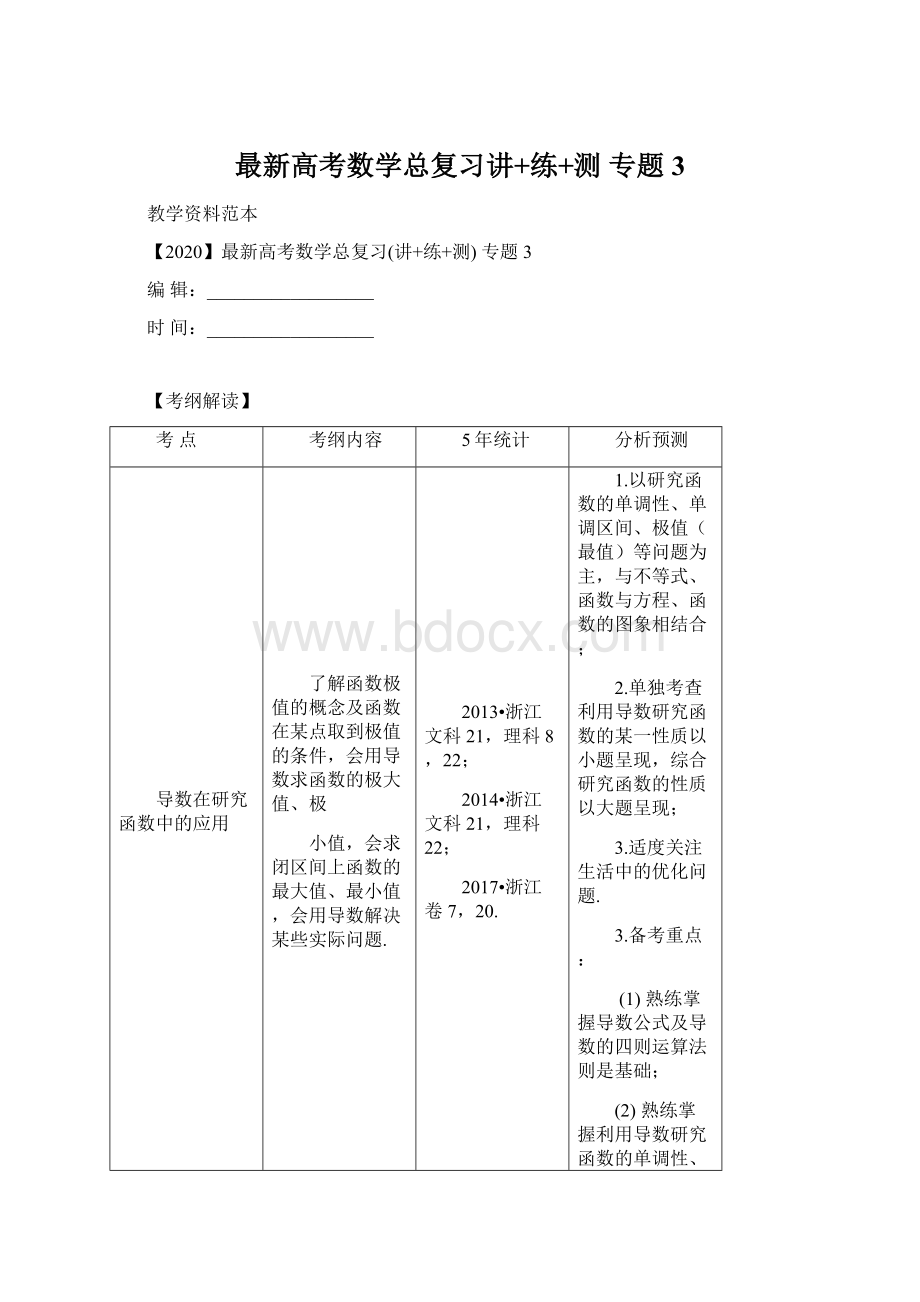
【答案】D

2．与函数零点有关的参数范围问题

1．方程有实根函数的图象与轴有交点函数有零点．

2．求极值的步骤：

①先求的根（定义域内的或者定义域端点的根舍去）；

②分析两侧导数的符号：

若左侧导数负右侧导数正，则为极小值点；

若左侧导数正右侧导数负，则为极大值点.

3．求函数的单调区间、极值、最值是统一的，极值是函数的拐点，也是单调区间的划分点，而求函数的最值是在求极值的基础上，通过判断函数的大致图像，从而得到最值,大前提是要考虑函数的定义域.

4．函数的零点就是的根，所以可通过解方程得零点，或者通过变形转化为两个熟悉函数图象的交点横坐标.

【20xx新课标1卷】已知函数有两个零点.

（I）求a的取值范围；

（II）设x1,x2是的两个零点,证明：

.

【答案】

【解析】

（Ⅰ）．

（i）设,则,只有一个零点．

（ii）设,则当时,；

当时,．所以在上单调递减,在上单调递增．

又,,取满足且,则

故存在两个零点．

（Ⅱ）不妨设,由（Ⅰ）知,,在上单调递减,所以等价于,即．

由于,而,所以

．

设,则．

所以当时,,而,故当时,．

从而,故．

3．与不等式恒成立、有解、无解等问题有关的参数范围问题

不等式的恒成立问题和有解问题、无解问题是联系函数、方程、不等式的纽带和桥梁，也是高考的重点和热点问题，往往用到的方法是依据不等式的特点，等价变形，构造函数，借助图象观察，或参变分离，转化为求函数的最值问题来处理．

：

设，函数，若对任意的，都有成立，则的取值范围为．

4．利用导数证明、解不等式问题

无论不等式的证明还是解不等式，构造函数，运用函数的思想，利用导数研究函数的性质（单调性和最值），达到解题的目的，是一成不变的思路，合理构思，善于从不同角度分析问题，是解题的法宝.

【20xx课标II，理】已知函数，且。

（1）求；

（2）证明：

存在唯一的极大值点，且。

（1）；

（2）证明略。

（2）由

（1）知，。

设，则。

当时，；

当时，，

所以在单调递减，在单调递增。

【考点深度剖析】

导数是研究函数性质的重要工具，它的突出作用是用于研究函数的单调性、极值与最值、函数的零点等．从题型看，往往有一道选择题或填空题，有一道解答题.其中解答题难度较大，常与不等式的证明、方程等结合考查，且有综合化更强的趋势．

【重点难点突破】

考点1利用导数研究函数的图象与性质

【1-1】【20xx河南开封10月月考】函数y=4cosx-e|x|（e为自然对数的底数）的图象可能是

ABCD

:

【答案】A

【解析】函数为偶函数，图象关于轴对称，排除B、D，若时，，当，当时，

，，，则，函数在上为减函数，选A.

【1-2】【20xx·

全国卷Ⅰ】函数y＝2x2－e|x|在[－2,2]的图象大致为（　　）

【答案】D

【领悟技法】

导数图象与原函数图象的关系：

若导函数图象与轴的交点为，且图象在两侧附近连续分布于轴上下方，则为原函数单调性的拐点，运用导数知识来讨论函数单调性时，由导函数的正负，得出原函数的单调区间．

【触类旁通】

【变式一】【20xx江西新余二模】将函数图象上各点的横坐标伸长为原来的2倍（纵坐标不变）后得到的图象，设，则的图象大致为（）

【变式二】【20xx·

丽水模拟】设函数f（x）在R上可导，其导函数为f′（x），且函数y＝（1－x）f′（x）的图象如图所示，则下列结论中一定成立的是（　　）

A．函数f（x）有极大值f

（2）和极小值f

（1）

B．函数f（x）有极大值f（－2）和极小值f

（1）

C．函数f（x）有极大值f

（2）和极小值f（－2）

D．函数f（x）有极大值f（－2）和极小值f

（2）

【解析】由题图，当x＜－2时，f′（x）＞0；

当－2＜x＜1时，f′（x）＜0；

当1＜x＜2时，f′（x）＜0；

当x＞2时，f′（x）＞0.由此可以得到函数f（x）在x＝－2处取得极大值，在x＝2处取得极小值．

考点2与函数零点有关的参数范围问题

【2-1】【20xx浙江杭州二模】设方程（，为自然对数的底数），则（）

A.当时，方程没有实数根B.当时，方程有一个实数根

C.当时，方程有三个实数根D.当时，方程有两个实数根

【2-2】【20xx课标3，理11】已知函数有唯一零点，则a=

A．B．C．D．1

【答案】C

试题分析：

函数的零点满足，

设，则，

当时，，当时，，函数单调递减，

当时，，函数单调递增，

当时，函数取得最小值，

设，当时，函数取得最小值，

1.确定零点的个数问题：

可利用数形结合的办法判断交点个数，如果函数较为复杂，可结合导数知识确定极值点和单调区间从而确定其大致图象.

2.方程的有解问题就是判断是否存在零点的问题，可参变分离，转化为求函数的值域问题处理.

3.与函数零点有关的参数范围问题，往往利用导数研究函数的单调区间和极值点，并结合特殊点，从而判断函数的大致图像，讨论其图象与轴的位置关系，进而确定参数的取值范围；

或通过对方程等价变形转化为两个函数图象的交点问题．

【变式一】【20xx湖南长沙二模】已知函数是定义在上的奇函数，且当时，，则对任意，函数的零点个数至多有（）

A.3个B.4个C.6个D.9个

【解析】当时,由此可知在上单调递减，在上单调递增，,且,数是定义在上的奇函数，，而时，,所以的图象如图，令,则，由图可知，当时方程至多3个根，当时方程没有根，而对任意，至多有一个根，从而函数的零点个数至多有3个.

【变式二】【20xx安徽阜阳二模】已知函数是自然对数的底数）.

（1）当是，求证：

；

（2）若函数有两个零点，求的取值范围.

（Ⅰ）见解析;

（Ⅱ）

试题解析：

（Ⅰ），

.得：

且在上单增，在上单减

故等价于在上有唯一极大值点

得：

故

令

，则

又在上单增，由，得

综上，

考点3与不等式恒成立、有解、无解等问题有关的参数范围问题

【3-1】若不等式对恒成立，则实数的取值范围是.

【答案】

所以在上是增函数，在是减函数.所以，所以.

（2）令，则，因为，所以，所以易知，所以在上是增函数.易知当时，，故在上无最小值，所以在上不能恒成立.综上所述，，即实数的取值范围是.

【3-2】已知函数．

（1）求在上的最小值；

（2）若关于的不等式只有两个整数解，求实数的取值范围．

（1）；

（2）.

∴若，的最小值为，．．．4分若，的最小值为，

综上，当时，的最小值为；

当，的最小值为

（2）由

（1）知，的递增区间为，递减区间为，

且在上，又，则．又．

∴时，由不等式得或，而解集为，整数解有无数多个，不合题意；

时，由不等式得，解集为，

整数解有无数多个，不合题意；

时，由不等式得或，

∵解集为无整数解，

若不等式有两整数解，则，

∴

综上，实数的取值范围是

含参数的不等式恒成立、有解、无解的处理方法：

①的图象和图象特点考考虑；

②构造函数法，一般构造，转化为的最值处理；

③参变分离法，将不等式等价变形为，或，进而转化为求函数的最值.

【变式一】已知函数，若存在，使得不等式成立，则实数的取值范围为（）

A．B．

C．D．

【变式二】【20xx福建三明5月质检】已知函数，．

（Ⅰ）当时，求证：

过点有三条直线与曲线相切；

（Ⅱ）当时，，求实数的取值范围．

（I）详见解析；

（II）.

解法一：

（Ⅰ）当时，，

设直线与曲线相切，其切点为，

则曲线在点处的切线方程为：

，

因为切线过点，所以，

即，

∵，∴，

设，

∵，，，

∴在三个区间上至少各有一个根

又因为一元三次方程至多有三个根，所以方程恰有三个根，

故过点有三条直线与曲线相切．

（1）当时，∵，∴，从而（当且仅当时，等号成立）

∴在上单调递增，

又∵，∴当时，，从而当时，，

∴在上单调递减，又∵，

从而当时，，即

于是当时，．

（2）当时，令，得，∴，

故当时，，

∴在上单调递减，

又∵，∴当时，，

从而当时，，

解法二：

则曲线在点处的切线方程为，

∵，∴

设，则，令得

当变化时，，变化情况如下表：

+

-

↗

极大值

↘

极小值

考点4利用导数证明、解不等式问题

【4-1】若的定义域为，恒成立，，则解集为（）

A．B．C．D．

【答案】B

【解析】构造函数，则，所以函数在定义域上单调递增，又，所以解集为.

【4-2】【20xx浙江温州二模】.证明：

（1）当，；

（2）对任意，当时，.

（1）详见解析；

（2）详见解析.

【解析】试题解析：

证明：

（1）考虑函数，，

则的导数，

从而，

故在内递减，在内递增，

因此对任意，都有，

即（当且仅当时，等号成立）①，

所以当时，，即；

（2）由①可知当时，，

即当时，②；

当时，③.

令函数，，

注意到，故要证②与③，只需证明在内递减，在内递增.

1.利用导数方法证明不等式f（x）>

g（x）在区间D上恒成立的基本方法是构造函数h（x）＝f（x）－g（x），然后根据函数的单调性，或者函数的最值证明函数h（x）>

0，其中一个重要技巧就是找到函数h（x）在什么地方可以等于零，这往往就是解决问题的一个突破口.

2.利用导数解不等式的基本方法是构造函数，通过研究函数的单调性，从而解不等式的方法.

【变式一】【20xx广东佛山二模】设函数，其中，是自然对数的底数.

（Ⅰ）若是上的增函数，求的取值范围；

（Ⅱ）若，证明：

.

（Ⅰ）;

（Ⅱ）见解析.

【解析】试题分析：

（I）由于函数单调递增，故导函数恒为非负数，分离常数后利用导数求得的最小值，由此得到的取值范围；

（II）将原不等式，转化为，令，求出的导数，对分成两类，讨论函数的最小值，由此证得，由此证得.

令，，是上的减函数，

又，故1是的唯一零点，

当，，，递增；

当，，，递减；

故当时，取得极大值且为最大值，

所以，即的取值范围是.

（Ⅱ）.

令（），以下证明当时，的最小值大于0.

求导得.

①当时，，；

②当时，，令，

则，又，

取且使，即，则，

因为，故存在唯一零点，

即有唯一的极值点且为极小值点，又，

【变式二】【20xx课标3，理21】已知函数.

（1）若，求a的值；

（2）设m为整数，且对于任意正整数n，求m的最小值.

（2）

【易错试题常警惕】

易错典例：

已知函数.

（Ⅰ）求的单调区间；

（Ⅱ）设，若对任意，均存在，使得＜，求的取值范围．

易错分析：

（Ⅰ）忽视定义域致误；

（Ⅱ）对全称量词和特称量词理解不深刻致误．

正确解析：

（Ⅰ）.①当时，，，在区间上，；

在区间上，故的单调递增区间是，单调递减区间是.

②当时，，在区间和上，；

在区间上，

故的单调递增区间是和，单调递减区间是.

③当时，，故的单调递增区间是.

④当时，，

在区间和上，；

故的单调递增区间是和，单调递减区间是.

②当时，在上单调递增，在上单调递减，

故.

由可知，，，

所以，，，

综上所述，,

温馨提醒：

（1）研究函数问题应竖立定义域优先原则；

（2）任意，指的是区间内的任意一个自变量；

存在，指的是区间内存在一个自变量，故本题是恒成立问题和有解问题的组合.

【学科素养提升之思想方法篇】

——————化抽象为具体——数形结合思想

数形结合是一种重要的数学思想方法，包含“以形助数”和“以数辅形”两个方面，其应用大致可以分为两种情形：

或者是借助形的生动和直观性来阐明数之间的联系，即以形作为手段，数为目的，比如应用函数的图像来直观地说明函数的性质；

或者是借助于数的精确性和规范严密性来阐明形的某些属性，即以数作为手段，形作为目的，如应用曲线的方程来精确地阐明曲线的几何性质. 

数形结合的思想，其实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化，它可以使代数问题几何化，几何问题代数化.在运用数形结合思想分析和解决问题时，要注意三点：

第一要彻底明白一些概念和运算的几何意义以及曲线的代数特征，对数学题目中的条件和结论既分析其几何意义又分析其代数意义；

第二是恰当设参、合理用参，建立关系，由数思形，以形想数，做好数形转化；

第三是正确确定参数的取值范围.,

在解答导数问题中，主要存在两类问题，一是“有图考图”，二是“无图考图”，如：

【典例1】已知是常数，函数的导函数的图像如图所示，则函数的图像可能是（）

【典例2】已知函数（a为常数，e为自然对数的底数）的图象在点A（e,1）处的切线与该函数的图象恰好有三个公共点，则实数a的取值范围是_____.