SPC统计制程品管.doc
《SPC统计制程品管.doc》由会员分享,可在线阅读,更多相关《SPC统计制程品管.doc(37页珍藏版)》请在冰豆网上搜索。
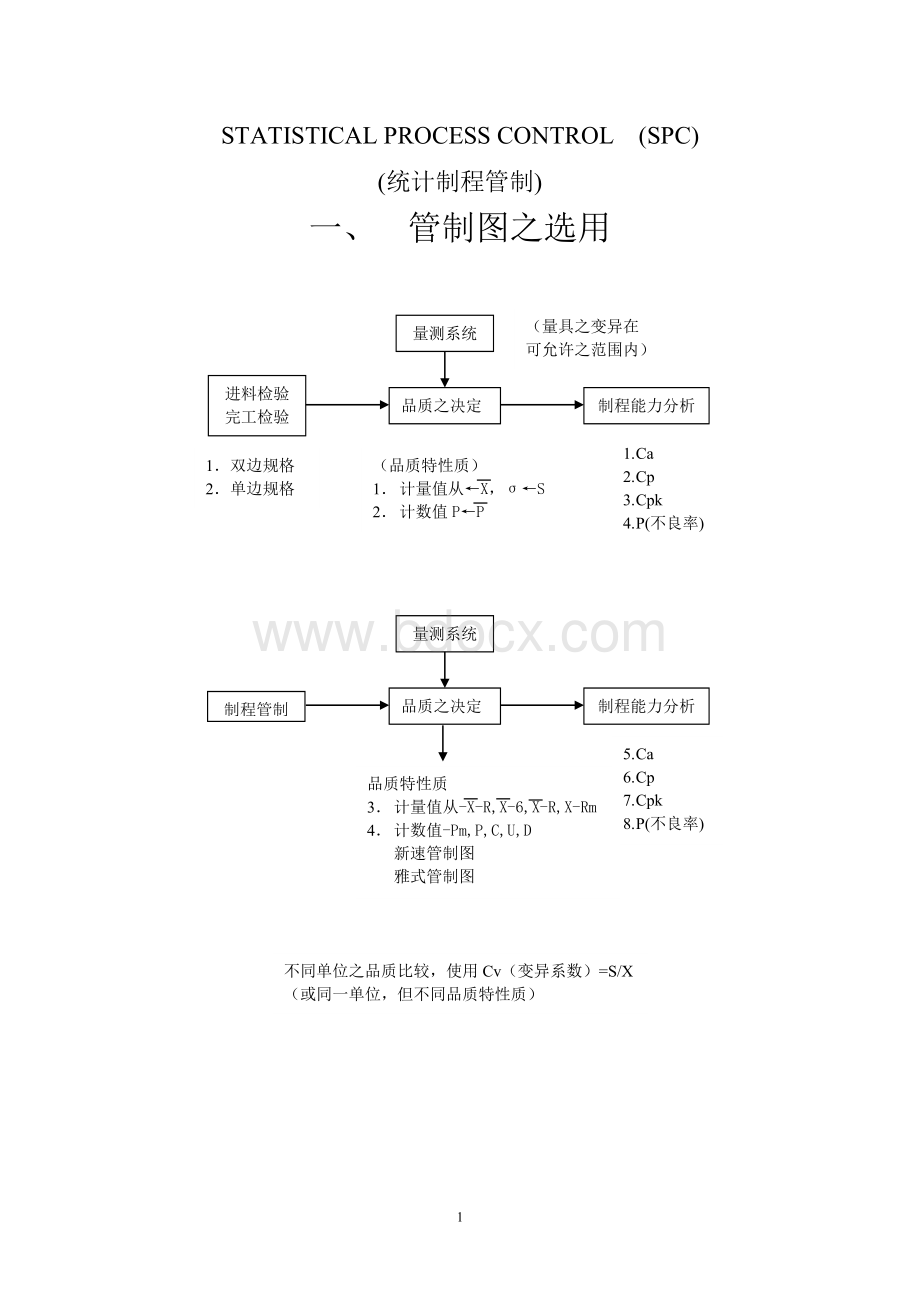
STATISTICALPROCESSCONTROL(SPC)
(统计制程管制)
一、管制图之选用
量测系统
(量具之变异在
可允许之范围内)
品质之决定
进料检验
完工检验
制程能力分析
1.双边规格
2.单边规格
(品质特性质)
1.计量值从←X,σ←S
2.计数值P←P
1.Ca
2.Cp
3.Cpk
4.P(不良率)
量测系统
品质之决定
制程管制
制程能力分析
品质特性质
3.计量值从-X-R,X-6,X-R,X-Rm
4.计数值-Pm,P,C,U,D
新速管制图
雅式管制图
5.Ca
6.Cp
7.Cpk
8.P(不良率)
不同单位之品质比较,使用Cv(变异系数)=S/X
(或同一单位,但不同品质特性质)
37
以管制图进行制程能力分析
一组数据之变化情形,除了可以用图形法来表示外,数量化之描述亦以提供有用之情报。
数据之量化表示有很多种,常用的有平均数(mean)、中位数(median)、众数(mode)、变异数(variance)、标准差(standarddeviation)。
1.平均数
假设X1,X2,…,Xn为样本中之观测值,样本数据之集中趋势可由样本平均数来衡量,样本平均数定义为
2.变异数
变异数是用来衡量数据之散布情形。
样本变异数S2为
S2=
计数值管制图
1.不良率管制图(pchart)
CLp=
UCLp=
LCLp=
2.不良数管制图(pnchart)
CLpn=
UCLpn=
LCLpn=
(σpn=)
3.缺点数管制图(cchart),样本大小相同
CLc=
UCLc=
LCLc=
4.单位缺点数(uchart),样本大小不相同
CLu=
UCLu=
LCLu=
计量值管制图
管制图
管制图类别
群体之μ及σ未知时
群体之μ及σ已知时
平均值管制图
全距管制图
CLR=d2σ
UCLR=D2σ
LCLR=D1σ
-S管制界限公式
图别
群体情况未知
群体情况已知
平均值管制图
CLX=μ
UCLX=μ+Aσ
LCLX=μ-Aσ
标准差管制图
CLS=C2σ
UCLS=B2σ
LCLS=B1σ
管制图
图别
群体情况未知
群体情况已知
中位值管制图
CLX=μ
全距管制图
CLR=d2σ
UCLR=D2σ
LCLR=D1σ
X-Rm管制图
X管制图 管制图
机遇原因之变异
(commoncause)
非机遇原因之变异
(specialcause)
1.大量之微小原因所引起。
2.不管发生何种之机遇原因,其个别之变异极为微小。
3.几个较为代表性之机遇原因如下:
(1)原料之微小变异。
(2)机遇之微小振动。
(3)机器测定时不十分精确之作法。
4.实际上要除去制程上之机遇变异原因,是件非常不经济之处置。
1.一个或少数几个较大原因所引起。
2.任何一个非机遇原因,都可能发生大之变异。
3.几个较为代表性之非机遇原因如下:
(1)原料群体之不良。
(2)不完全之机遇调整。
(3)新手之作业员。
4.非机遇原因之变异不但可以找出其原因,并且除去这些原因之处置,在经济观点上讲常是正确者。
管制图之选定原则
管制图之选定
资料性
质?
资料是不良数或缺点数?
样本大小n≥2?
中心线CL之性质?
n是否
一定?
单位大小是否一定?
n是否较大?
X―σ
图
X―R
图
X―Rm
图
―R
图
pn
图
p
图
C
图
u
图
计量值
计数值
n≥2
n=1
不良数
缺点数
一定
不一定
一定
不一定
X
n=2~5
0管制图之比较
优点
缺点
计量值管制图
1.用于制程之管制,甚灵敏,很容易调查事故发生之原因,因此可以预测将发生之不良状况。
2.能及时并正确地找出不良原因,可使品质稳定,为最优良之管制工具。
在制造成过程需要经常抽样并邓以测定以及讲算,且需点上管制图,较为麻烦而费时间。
计数值管制图
1.只有生产完成后,才抽本,将其区分为良品与不良品,所需数据,能以简单方法获得之。
2.对于工厂整个品质情况了解非常方方便。
只靠此种管制图,有时无法寻求不良之真正原因,而不能及时采取处理措施,而延误时机。
管制图之绘制流程(步骤)
决定管制项目
标准化
搜集数据
绘制解析用管制图
解析
安定状态?
绘制直方图
满足规格?
管制用管制图
追求、去除异常原因以达安定状态。
检讨机械、设备等等
提升制程能力
满足
不满足
安定状态
非安定状态
1.检定规则一:
有单独一个点子,出现在三个标准差区域之外者。
(有一点落在管制界限之外者)。
如图22。
UCL
CL
+3σ
+2σ
+1σ
A区
B区
C区
图22
2.检定规则二:
连续三点之中有两点落在A区或甚至于A区以外者。
(在中心线之同侧三个连续点中有两点出现在两个标准差之外者)。
如图23。
UCL
CL
+3σ
+2σ
+1σ
A区
B区
C区
图23
3.检定规则三:
连续五点之中有四点落在B区或甚至于以外者。
(在中心线同侧,五个连续点中有四个点超出一个标准差者)。
如图24。
UCL
CL
+3σ
+2σ
+1σ
A区
B区
C区
图24
4.检定规则四:
连续有八点落在C区或甚至于在C区以处者。
(八个连续点子落在C区或其中连续七点出现在中心线之同一侧者)。
UCL
CL
+3σ
+2σ
+1σ
A区
B区
C区
图25
5.检定规则五:
连续几点同一方向时:
(如下图)
(1)连续五点继续上升(或下降)——注意以后动态。
(如图26a)
(2)连续六点继续上升(或下降)——开始调查原因。
(如图26b)
(3)连续七点继续上升(或下降)——必有原因,应立即采取措施。
(如图26c)
图26a
图26b
图26c
UCL
CL
+3σ
+2σ
+1σ
LCL
-1σ
-2σ
-3σ
不合格率管制图(P管制图)
〔例〕考虑某一生产铝箔包之机器,此机器系以三班制连续生产,其考虑之品质特性为铝箔包之缝合是否良好。
为了设立管制图,30组大小为n=50之样本从三班以半小时之间隔收集,其数据显示在表5-1。
从这些数据可建立一试用管制图,由于30组样本共包含个不合格品,因此
===0.2313
利用当做是制程不合格率之估计值,可得管制界限为
=0.2313=0.23130.1789
亦即
上管制界限=0.4102
下管制界限=0.0524
表5-1试用管制界限数据,n=50
样本
不合格品数
不合格率
样本
不合格品数
不合格率
1
8
0.16
16
8
0.16
2
12
0.24
17
8
0.16
3
8
0.16
18
6
0.12
4
10
0.2
19
13
0.26
5
6
0.12
20
10
0.2
6
7
0.14
21
20
0.4
7
16
0.32
22
18
0.36
8
9
0.18
23
25
0.5
9
14
0.28
24
15
0.3
10
10
0.2
25
9
0.18
11
7
0.14
26
12
0.24
12
6
0.12
27
7
0.14
13
22
0.44
28
14
0.28
14
12
0.24
29
9
0.18
15
18
0.36
30
8
0.16
不合格品数总和=347,=0.2313
样本编号
样本不合格率
0.4102
0.2313
0.0524
样本编号
样本不合格率
0.4102
0.2313
0.0524
P管制图
平均值:
0.2143
标准差:
0.0580
样本大小:
50
样本编号
0.3884
0.2143
0.0402
样本不合格率
P管制图
平均值:
0.2143
标准差:
0.0580
样本大小:
50
机器调整后之数据,n=50
样本
不合格品数
不合格率
样本
不合格品数
不合格率
31
8
0.16
43
3
0.06
32
6
0.12
44
6
0.12
33
11
0.22
45
7
0.14
34
5
0.10
46
4
0.08
35
6
0.12
47
8
0.16
36
4
0.08
48
5
0.10
37
6
0.12
49
6
0.12
38
4
0.08
50
7
0.14
39
7
0.14
51
4
0.08
40
6
0.12
52
6
0.12
41
3
0.06
53
4
0.08
42
4
0.08
54
5
0.10
不合格品数总和=135,=0.1125
P管制图
平均值:
0.2143
标准差:
0.0580
样本大小:
50
0.3884
0.2143
0.0402
样本编号
样本不合格率
机器调整后之管制图
检定:
1=0.2143,α=0.05
2=0.1125
Ho:
P1-P2=0
H1:
P1-P2>0
Z=
=0.1673
所以
Z==6.933
Z=6.933>Zα=1.645,
故acceptH1,显示不合格率经调校后已有显著改善。
由于改善成功,可以利用(样本31#~54#)之数据重新计算管制界限。
Cp=
=0.1125
UCL=
LCL=(设为零)
新的不合格率数据,n=50
样本
不合格品数
不合格率
样本
不合格品数
不合格率
55
7
0.14
75
6
0.12
56
8
0.16
76
8
0.16
57
5
0.10
77
11
0.22
58
6
0.12
78
9
0.18
59
4
0.08
79
7
0.14
60
5
0.10
80
4
0.08
61
2
0.04
81
5
0.10
62
3
0.06
82
2
0.04
63
4
0.08
83
1
0