已知一边一角构造全等三角形Word文档下载推荐.docx

已知一边一角构造全等三角形Word文档下载推荐.docx

《已知一边一角构造全等三角形Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《已知一边一角构造全等三角形Word文档下载推荐.docx（9页珍藏版）》请在冰豆网上搜索。

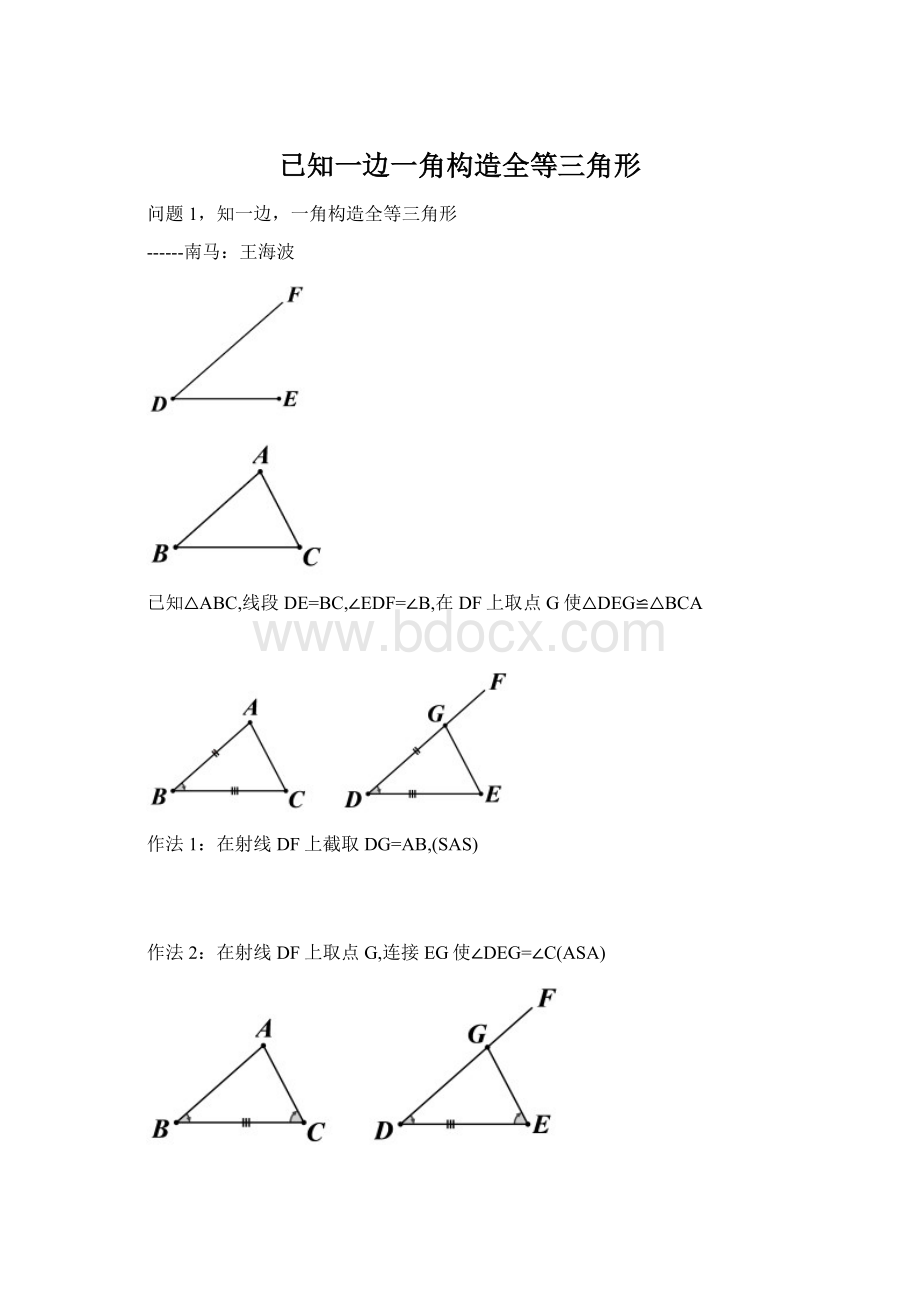
作法2：

在射线DF上取点G,连接EG使∠DEG=∠C（ASA）

作法3：

1.在△ACB中,∠ACB=90°

，且S△ACB=24,AC>

BC,以AB为边做△ADB,点D与点C在AB的同侧,∠ADB=90°

，AD=BD,做DE⊥BC于点E,若DE=1,

则AC=

2.已知在△ABC中,∠B=30°

，点D、E分别在AB、BC边上，连接DE,若∠ADE=∠C,AC=DE,若AD=5,S△BDE=12,BE>

BD则BE=

3.如图在△ABC中AD、BE是高，连接DE,AD=BD,若AE=2,S△BDE=12,

则BE=

4.如图在△ACB中,∠C=90°

点O是AB边的中点E、F两点分别在AC边、BC边上,∠EOF=90°

连接OE、OF、EF,过点B做BG⊥OF于点G,∠AOE=∠BOF

若S△EOF=12,GF=1,OF>

OE,则OE=

5.如图在△ABC中,点D在AB边上,DE⊥AC于点E,点F在AC的延长线上,连接DF交BC于点G,DF=BC,∠BGF=2∠A,,AE=2，CF=

6.如图在四边形ABCD中，连接对角线AC，∠DAC=90°

，∠ACB=60°

，∠D=∠BAC,AB=CD,AC=8,AD=3,则BC=

7.如图，在等边△ABC中，D为BC边上一点，E为AC上一点，且∠ADB+∠EDC=120°

AD:

DE=8:

5,BC=16,则BD的长为_____.

8.如图，在等边△ABC中，点D是BC中点，点E在BA的延长线上，ED=EC，AC和ED交于点F，若AE=

，则CF=__________.

9.如图，△ABC中，∠ACB=60°

，点D在AB边上，CD=14,∠BDC=60°

，延长CB至点E,使CE=AC,过点E作EF⊥CD于点F，交AB于点G,AD=3DG则DF=。

10.如图在△ABC中,∠BAC=90°

AD⊥BC于D,AF⊥BE于G,∠AFD=∠C,AF=AB,AD=2DF，∠DAF=∠CBE,BG=3,则AE=

11.如图在△ABC中,AB=10,AC=6,CD∥AB,CD=AC,在AC上取点E,连接DE交BC于点F,DE=BC,∠DFB=30°

，则S△ABC=

12.如图在△ABC中，∠BAC=90°

AB=AC,点E在BC上，点D、F在AC上,连接AD、AE、EFAE⊥AD于G，AD=CF，求证∠AEB=∠CEF

13.如图，在△ABC中,BG是高，BE∥AC,BE=AB,在AB边上取点D,连接DE,DE=BC,DE与BC交于点F,若∠CFE=∠A,S△ABC=5S△BDE,AG=4,则CG=

14.如图在△ABC中,AB=AC,点D在BC上,连接AD，作BE⊥AD于点E，∠C=∠BAD，AE=2DE,BC=4,则AD=

15.如图在∆ABC中，点D在AC边上,点F在BC边上,BD=CD,∠A=∠BDF=∠BFD,S∆CDF:

S∆ABD=2:

3,AG=1,则BG=

16.如图在∆ABC中，点D在AC边上,点E是BC边中点,BC=CD,∠CED=2∠A，∆CDE的周长为9则AD=

17.如图，在△ABC中∠ACB=∠ABC=75°

∠ADC=150°

S△ABD=

则AD=

18.如图，△ACB中,AC=BC,∠ACB=90°

点D在AB边上,点E在AC边上,连接CD,连接BE交于G,若CD⊥BE,BG=6DG,CG=3,则S△ACD=

19.如图,在△ABC中,∠ABC=135°

分别过A、B两点做AC、BC的垂线,交于点D,再做AE⊥BD于点E,若BD=2BC,BE=1,则AC=

20.如图：

在△ABD中,AG是高,点F在AD边上,点C在BD边上,连接BF,AB=BC,∠AFB=∠ABD,过点C做AB的平行线与射线BF交于点E,S△BCE:

S△ABD=2:

3,BG=1,则CE=

21.已知在△BEC中,CE=CB,EF⊥BC于F,延长BE至点A使BE=AE,再延长BC至点D,连接DE、AC,且∠B=∠A+∠D,求证;

CD=2BF

22.如图在等边∆ABC中,点D在BC上,点E在CA的延长线上,连接BE、AD,若∠ADB=2∠E,求证：

AE+CD=AD

23.如图在△ABC中，∠C:

=300,点D在BC边上，连接AD,BD=AB,在AC上截取AE=AB，在AB边上取点F,连接EF交AD于G，再做AN⊥EF于点N若∠AGF:

60°

，若S△AND=18则AD=

24.如图在△ABC中AB=AC．∠BAC=45°

，在其内部取一点D，连接AD、BD、CD，AD⊥CD．∠ADB=∠BDC．AD=2,S△ADC=24,则AD=

25.如图，在△ABC中,∠BAC=45°

，BG是高,在AC上取点D,在BA的延长线上取点E,连接DE,∠E=∠C,DE=BC,若S△ABC=20,AE=2,则AC=

26.如图在△ABC中,∠ABC=45°

，在AB上取点E,在CB的延长线上取点D,连接DE,∠DEB=∠A,DE=AC,S△ABC=20,BE=2,则AB=

27.如图：

在△ABC中，∠ACB=90°

，AC=BC，点D在AB上连接CD,

若AD=AC,S△BCD=9，则CD=

28.如图，在△ABC中,AC=BC,AD是中线,做BE⊥AB交射线AD于点E,连接CE,∠BCE=∠CAD,△ECD的周长为3,△ACD的周长为5,则AB=

29.如图,在△ABC中,AC=BC，点D是△ABC外一点,连接CD、BD、AD，若∠BCD=∠CAD,∠ADC=90°

，S△BCD=18,则BD=

30.如图在△ABC中,AC=BC，点D在BC上;

点E在AB上,连接AD、CE，AD与CE交于点G,若∠AGE=∠ACB,∠ADC=2∠AEC，EG=3,AG=5,则CG=