三年高考数学文真题分类解析专题13等差与等比数列Word下载.docx

三年高考数学文真题分类解析专题13等差与等比数列Word下载.docx

《三年高考数学文真题分类解析专题13等差与等比数列Word下载.docx》由会员分享，可在线阅读，更多相关《三年高考数学文真题分类解析专题13等差与等比数列Word下载.docx（18页珍藏版）》请在冰豆网上搜索。

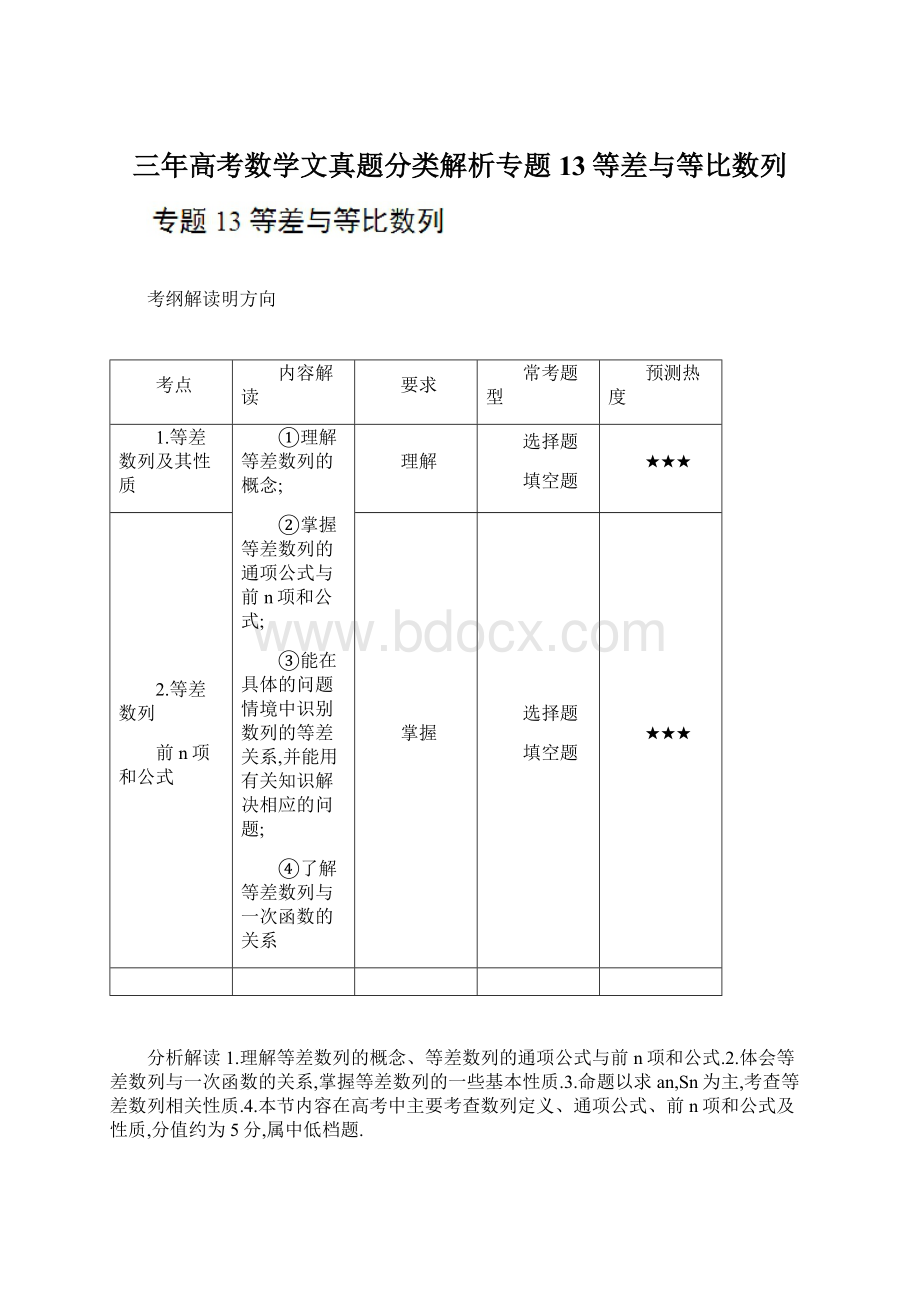
解答题

2.等比数列前

n项和公式

分析解读1.理解等比数列的概念、掌握等比数列的通项公式和前n项和公式.2.体会等比数列与指数函数的关系.3.求通项公式、求前n项和及等比数列相关性质的应用是高考热点.

2018年高考全景展示

1.【2018年文北京卷】】“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于

.若第一个单音的频率f，则第八个单音频率为

A.

B.

C.

D.

【答案】D

【解析】分析：

根据等比数列的定义可知每一个单音的频率成等比数列，利用等比数列的相关性质可解.

详解：

因为每一个单音与前一个单音频率比为

，所以

，又

，则

，故选D.

点睛：

此题考查等比数列的实际应用，解决本题的关键是能够判断单音成等比数列.等比数列的判断方法主要有如下两种：

（1）定义法，若

（

）或

），数列

是等比数列；

（2）等比中项公式法，若数列

中，

且

），则数列

是等比数列.

2.【2018年文北京卷】设

是等差数列，且

.

（Ⅰ）求

的通项公式；

（Ⅱ）求

【答案】

（I）

（II）

（1）设公差为

，根据题意可列关于

的方程组，求解

，代入通项公式可得；

（2）由

（1）可得

，进而可利用等比数列求和公式进行求解.

等差数列的通项公式及前

项和共涉及五个基本量

，知道其中三个可求另外两个，体现了用方程组解决问题的思想.

3.【2018年全国卷Ⅲ文】等比数列

．

（1）求

（2）记

为

的前

项和．若

，求

（1）

或

（2）

（1）列出方程，解出q可得；

（2）求出前n项和，解方程可得m。

（1）设

的公比为

，由题设得

．由已知得

，解得

（舍去），

故

（2）若

．由

得

，此方程没有正整数解．

若

．综上，

本题主要考查等比数列的通项公式和前n项和公式，属于基础题。

4.【2018年新课标I卷文】已知数列

满足

，

，设

；

（2）判断数列

是否为等比数列，并说明理由；

（3）求

的通项公式．

（1）b1=1，b2=2，b3=4．

（2）{bn}是首项为1，公比为2的等比数列．理由见解析.（3）an=n·

2n-1．

（1）根据题中条件所给的数列

的递推公式

，将其化为an+1=

，分别令n=1和n=2，代入上式求得a2=4和a3=12，再利用

，从而求得b1=1，b2=2，b3=4．

（2）利用条件可以得到

，从而可以得出bn+1=2bn，这样就可以得到数列{bn}是首项为1，公比为2的等比数列．（3）借助等比数列的通项公式求得

，从而求得an=n·

该题考查的是有关数列的问题，涉及到的知识点有根据数列的递推公式确定数列的项，根据不同数列的项之间的关系，确定新数列的项，利用递推关系整理得到相邻两项之间的关系确定数列是等比数列，根据等比数列通项公式求得数列

的通项公式，借助于

的通项公式求得数列

的通项公式，从而求得最后的结果.

2017年高考全景展示

1.【2017浙江，6】已知等差数列{an}的公差为d，前n项和为Sn，则“d>

0”是“S4+S6>

2S5”的

A．充分不必要条件B．必要不充分条件

C．充分必要条件D．既不充分也不必要条件

【答案】C

【解析】

【考点】等差数列、充分必要性

【名师点睛】本题考查等差数列的前

项和公式，通过公式的套入与简单运算，可知

，结合充分必要性的判断，若

是

的充分条件，若

的必要条件，该题“

”

“

”，故为充要条件．

2.【2017江苏，9】等比数列

的各项均为实数,其前

项的和为

已知

则

=▲.

【答案】32

【解析】当

时，显然不符合题意；

当

时，

【考点】等比数列通项

【名师点睛】在解决等差、等比数列的运算问题时，有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;

二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现，是解决等差、等比数列问题既快捷又方便的工具，应有意识地去应用.但在应用性质时要注意性质的前提条件，有时需要进行适当变形.在解决等差、等比数列的运算问题时，经常采用“巧用性质、整体考虑、减少运算量”的方法.

3.【2017课标1，文17】记Sn为等比数列

的前n项和，已知S2=2，S3=-6．

（2）求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列．

，证明见解析．

试题分析：

（1）由等比数列通项公式解得

（2）利用等差中项证明Sn+1，Sn，Sn+2成等差数列．

【考点】等比数列

【名师点睛】等差、等比数列的性质是两种数列基本规律的深刻体现，是解决等差、等比数列问题既快捷又方便的工具，应有意识地去应用．但在应用性质时要注意性质的前提条件，有时需要进行适当变形．在解决等差、等比数列的运算问题时，经常采用“巧用性质、整体考虑、减少运算量”的方法．

4.【2017课标II，文17】已知等差数列

项和为

，等比数列

（1）若

（Ⅰ）

（Ⅱ）当

.当

【解析】试题分析：

（1）根据等差数列及等比数列通项公式，表示条件，得关于公差与公比的方程组，解方程组得公比，代入等比数列通项公式即可，

（2）由等比数列前三项的和求公比，分类讨论，求公差，再根据等差前三项求和.

【考点】等差、等比数列通项与求和

二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现，是解决等差、等比数列问题既快捷又方便的工具，应有意识地去应用.但在应用性质时要注意性质的前提条件，有时需要进行适当变形.在解决等差、等比数列的运算问题时，经常采用“巧用性质、整体考虑、减少运算量”的方法.

2016年高考全景展示

1.【2016高考新课标2文数】等差数列{

}中，

（Ⅰ）求{

}的通项公式；

（Ⅱ）设

，求数列

的前10项和，其中

表示不超过

的最大整数，如[0.9]=0,[2.6]=2.

（Ⅱ）24.

（Ⅰ）题目已知数列{

}是等差数列，根据通项公式列出关于

的方程，解方程求得

，从而求得

（Ⅱ）根据条件

的最大整数，求

，需要对

分类讨论，再求数列

的前10项和.

考点：

等差数列的性质，数列的求和.

【名师点睛】求解本题会出现以下错误：

①对“

的最大整数”理解出错；

2.【2016高考北京文数】

（本小题13分）

已知

是等差数列，

（2）设

的前n项和.

，）；

（Ⅰ）求出等比数列

的公比，求出

的值，根据等差数列的通项公式求解；

（Ⅱ）根据等差数列和等比数列的前

项和公式求数列

项和.

试题解析：

（I）等比数列

的公比

所以

设等差数列

的公差为

因为

，即

，）．

等差、等比数列的通项公式和前n项和公式，考查运算能力.

【名师点睛】1.数列的通项公式及前n项和公式都可以看作项数n的函数，是函数思想在数列中的应用.数列以通项为纲，数列的问题，最终归结为对数列通项的研究，而数列的前n项和Sn可视为数列{Sn}的通项.通项及求和是数列中最基本也是最重要的问题之一；

2.数列的综合问题涉及到的数学思想：

函数与方程思想（如：

求最值或基本量）、转化与化归思想（如：

求和或应用）、特殊到一般思想（如：

求通项公式）、分类讨论思想（如：

等比数列求和，

）等.

3.【2016高考四川文科】

（本小题满分12分）

已知数列{

}的首项为1，

为数列

的前n项和，

，其中q>

0，

.

（Ⅰ）若

成等差数列，求

（Ⅱ）设双曲线

的离心率为

，且

，求

（Ⅱ）

（Ⅰ）已知

的递推式

，一般是写出当

，两式相减，利用

，得出数列

的递推式，从而证明

为等比数列，利用等比数列的通项公式得到结论；

（Ⅱ）先利用双曲线的离心率定义得到

的表达式，再由

解出

的值，最后利用等比数列的求和公式求解计算.

（Ⅱ）由（Ⅰ）可知，

所以双曲线

的离心率

由

解得

.所以，

数列的通项公式、双曲线的离心率、等比数列的求和公式