八年级数学三角形中考真题专题练习汇总Word文档下载推荐.docx

八年级数学三角形中考真题专题练习汇总Word文档下载推荐.docx

《八年级数学三角形中考真题专题练习汇总Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《八年级数学三角形中考真题专题练习汇总Word文档下载推荐.docx（24页珍藏版）》请在冰豆网上搜索。

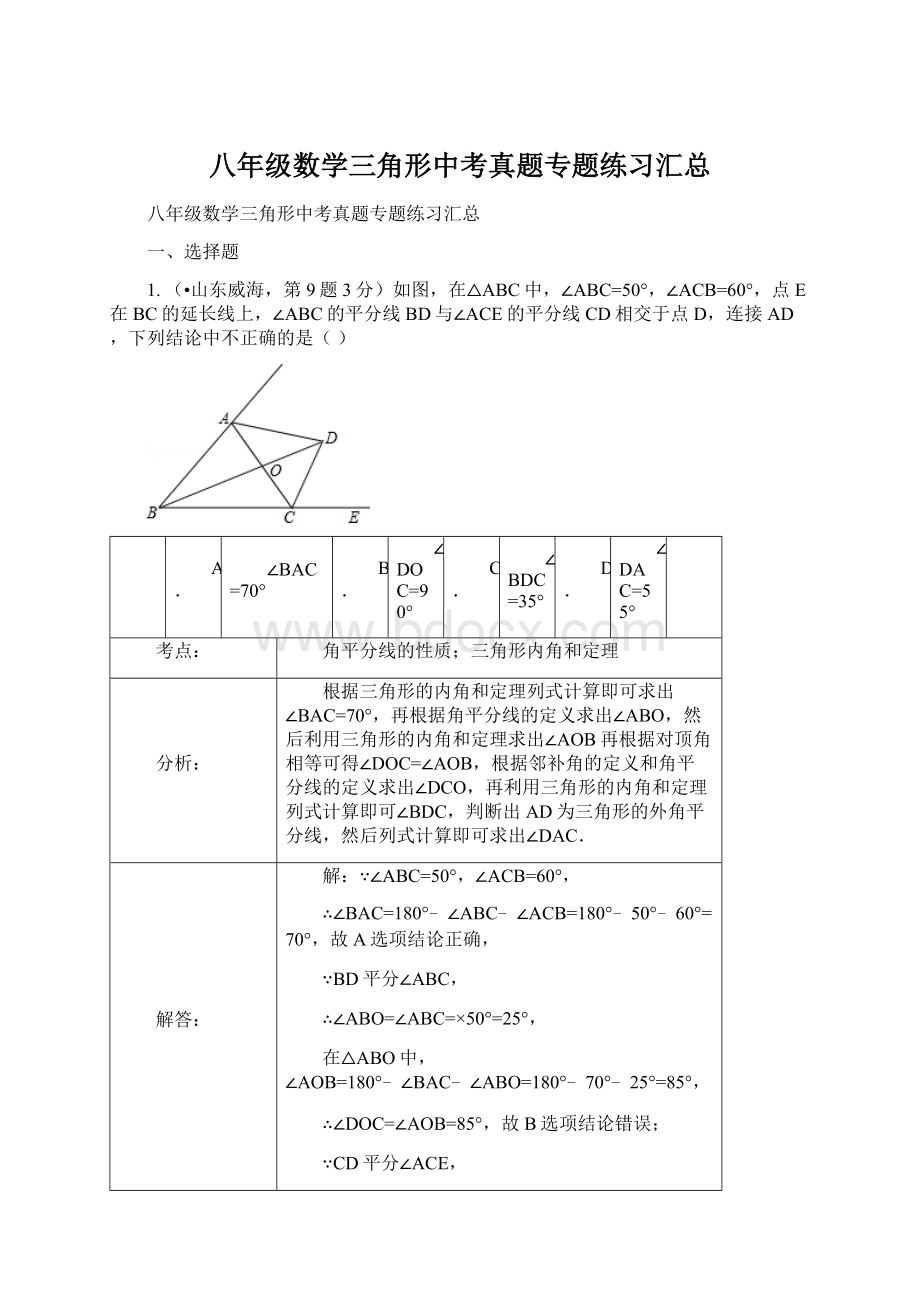
∴∠BDC=180°

﹣85°

=35°

，故C选项结论正确；

∵BD、CD分别是∠ABC和∠ACE的平分线，

∴AD是△ABC的外角平分线，

∴∠DAC=（180°

）=55°

，故D选项结论正确．

故选B．

点评：

本题考查了角平分线的性质，三角形的内角和定理，角平分线的定义，熟记定理和概念是解题的关键．

2.（•山东临沂,第3题3分）如图，已知l1∥l2，∠A=40°

，∠1=60°

，则∠2的度数为（　　）

40°

60°

80°

100°

平行线的性质；

三角形的外角性质．

根据两直线平行，内错角相等可得∠3=∠1，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．

∵l1∥l2，

∴∠3=∠1=60°

∴∠2=∠A+∠3=40°

+60°

=100°

．

故选D．

本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并准确识图是解题的关键．

3.（•江苏苏州,第6题3分）如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=80°

，则∠C的度数为（　　）

30°

45°

等腰三角形的性质

先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．

∵△ABD中，AB=AD，∠B=80°

∴∠B=∠ADB=80°

∴∠ADC=180°

﹣∠ADB=100°

∵AD=CD，

∴∠C=

=

=40°

本题考查的是等腰三角形的性质，熟知等腰三角形的两底角相等是解答此题的关键．

4．（•福建福州,第6题4分）下列命题中，假命题是【】

A．对顶角相等B．三角形两边和小于第三边

C．菱形的四条边都相等D．多边形的内角和等于360°

5．（·

台湾，第20题3分）如图，有一△ABC，今以B为圆心，AB长为半径画弧，交BC于D点，以C为圆心，AC长为半径画弧，交BC于E点．若∠B＝40°

，∠C＝36°

，则关于AD、AE、BE、CD的大小关系，下列何者正确？

（　　）

A．AD＝AEB．AE＜AEC．BE＝CDD．BE＜CD

由∠C＜∠B利用大角对大边得到AB＜AC，进一步得到BE＋ED＜ED＋CD，从而得到BE＜CD．

∵∠C＜∠B，

∴AB＜AC，

即BE＋ED＜ED＋CD，

∴BE＜CD．

考查了三角形的三边关系，解题的关键是正确的理解题意，了解大边对大角．

6.（·

云南昆明，第5题3分）如图，在△ABC中，∠A=50°

，∠ABC=70°

，BD平分∠ABC，则∠BDC的度数是（）

A.85°

B.80°

C.75°

D.70°

角平分线的性质，三角形外角性质.

首先角平分线的性质求得

的度数，然后利用三角形外角性质求得∠BDC的度数即可．

∠ABC=70°

，BD平分∠ABC

∠A=50°

∠BDC

故选A．

本题考查了三角形角平分线的性质和三角形外角性质.，属于基础题，比较简单．

7.（•泰州，第6题，3分）如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（　　）

1，2，3

1，1，

1，2，

解直角三角形

专题：

新定义．

A、根据三角形三边关系可知，不能构成三角形，依此即可作出判定；

B、根据勾股定理的逆定理可知是等腰直角三角形，依此即可作出判定；

C、解直角三角形可知是顶角120°

，底角30°

的等腰三角形，依此即可作出判定；

D、解直角三角形可知是三个角分别是90°

，60°

，30°

的直角三角形，依此即可作出判定．

A、∵1+2=3，不能构成三角形，故选项错误；

B、∵12+12=（

）2，是等腰直角三角形，故选项错误；

C、底边上的高是

，可知是顶角120°

的等腰三角形，故选项错误；

的直角三角形，其中90°

÷

=3，符合“智慧三角形”的定义，故选项正确．

故选：

考查了解直角三角形，涉及三角形三边关系，勾股定理的逆定理，等腰直角三角形的判定，“智慧三角形”的概念．

8.（•广西玉林市、防城港市，第10题3分）在等腰△ABC中，AB=AC，其周长为20cm，则AB边的取值范围是（　　）

1cm＜AB＜4cm

5cm＜AB＜10cm

4cm＜AB＜8cm

4cm＜AB＜10cm

等腰三角形的性质；

解一元一次不等式组；

三角形三边关系．

设AB=AC=x，则BC=20﹣2x，根据三角形的三边关系即可得出结论．

∵在等腰△ABC中，AB=AC，其周长为20cm，

∴设AB=AC=xcm，则BC=（20﹣2x）cm，

∴

解得5cm＜x＜10cm．

本题考查的是等腰三角形的性质，熟知等腰三角形的两腰相等是解答此题的关键．

9.（•湖南邵阳，第5题3分）如图，在△ABC中，∠B=46°

，∠C=54°

，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是（）

54°

根据三角形的内角和定理求出∠BAC，再根据角平分线的定义求出∠BAD，然后根据两直线平行，内错角相等可得∠ADE=∠BAD．

∵∠B=46°

﹣∠B﹣∠C=180°

﹣46°

﹣54°

=80°

∵AD平分∠BAC，

∴∠BAD=

∠BAC=

×

∵DE∥AB，

∴∠ADE=∠BAD=40°

故选C．

本题考查了平行线的性质，三角形的内角和定理，角平分线的定义，熟记性质与概念是解题的关键．

10．（·

台湾，第18题3分）如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A＝60°

，∠ACP＝24°

，则∠ABP的度数为何？

A．24B．30C．32D．36

根据角平分线的定义可得∠ABP＝∠CBP，根据线段垂直平分线上的点到两端点的距离相等可得BP＝CP，再根据等边对等角可得∠CBP＝∠BCP，然后利用三角形的内角和等于180°

列出方程求解即可．

∵直线M为∠ABC的角平分线，

∴∠ABP＝∠CBP．

∵直线L为BC的中垂线，

∴BP＝CP，

∴∠CBP＝∠BCP，

∴∠ABP＝∠CBP＝∠BCP，

在△ABC中，3∠ABP＋∠A＋∠ACP＝180°

即3∠ABP＋60°

＋24°

＝180°

解得∠ABP＝32°

本题考查了线段垂直平分线上的点到两端点的距离相等的性质，角平分线的定义，三角形的内角和定理，熟记各性质并列出关于∠ABP的方程是解题的关键．

11.（•湖北宜昌,第6题3分）已知三角形两边长分别为3和8，则该三角形第三边的长可能是（　　）

5

10

11

12

根据三角形的第三边大于两边之差，而小于两边之和求得第三边的取值范围，再进一步选择．

根据三角形的三边关系，得

第三边大于：

8﹣3=5，而小于：

3+8=11．

则此三角形的第三边可能是：

10．

本题考查了三角形的三边关系，即三角形的第三边大于两边之差，而小于两边之和，此题基础题，比较简单．

12.（•河北，第3题2分）如图，△ABC中，D，E分别是边AB，AC的中点．若DE=2，则BC=（　　）

2

3

4

三角形中位线定理．

根据三角形的中位线平行于第三边并且等于第三边的一半可得BC=2DE．

∵D，E分别是边AB，AC的中点，

∴DE是△ABC的中位线，

∴BC=2DE=2×

2=4．

本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理是解题的关键．

13、（•河北，第4题2分）如图，平面上直线a，b分别过线段OK两端点（数据如图），则a，b相交所成的锐角是（　　）

20°

70°

三角形的外角性质

根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．

a，b相交所成的锐角=100°

=30°

本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．

14.（•随州，第4题3分）如图，在△ABC中，两条中线BE、CD相交于点O，则S△DOE：

S△COB=（　　）

1：

2：

相似三角形的判定与性质；

三角形中位线定理

根据三角形的中位线得出DE∥BC，DE=

BC，根据平行线的性质得出相似，根据相似三角形的性质求出即可．

∵BE和CD是△ABC的中线，

∴DE=

BC，DE∥BC，

，△DOE∞△COB，

=（

）2=（

）2=

本题考查了相似三角形的性质和判定，三角形的中位线的应用，注意：

相似三角形的面积比等于相似比的平方，三角形的中位线平行于第三边，并且等于第三边的一半．

15.（•广东，第9题3分）一个等腰三角形的两边长分别是3和7，则它的周长为（　　）

17

15

13

13或17

由于未说明两边哪个是腰哪个是底，故需分：

（1）当等腰三角形的腰为3；

（2）当等腰三角形的腰为7；

两种情况讨论，从而得到其周长．

①当等腰三角形的腰为3，底为7时，3+3＜7不能构成三角形；

②当等腰三角形的腰为7，底为3时，周长为3+7+7=17．

故这个等腰三角形的周长是17．

本题考查的是等腰三角形的性质，在解答此题时要注意进行分类讨论．

二、填空题

1.（•山东威海，第15题3分）直线l1∥l2，一块含45°

角的直角三角板如图放置，∠1=85°

，则∠2=40°

．

根据两直线平行，同位角相等可得∠3=∠1，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4，然后根据对顶角相等解答．

∴∠3=∠1=85°

∴∠4=∠3﹣45°

﹣45°

∴∠2=∠4=40°

故答案为：

本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．

2．（•湖南怀化，第15题，3分）如图，在△ABC中，∠A=30°

，∠B=50°

，延长BC到D，则∠ACD=　80　°

∵∠A=30°

∴∠ACD=∠A+∠B=30°

+50°

80．

本题考查了三角形的一个外角等于与它不相邻的两个内角的和，熟记性质是解题的关键．

3.（•江苏盐城,第14题3分）如图，A、B两地间有一池塘阻隔，为测量A、B两地的距离，在地面上选一点C，连接CA、CB的中点D、E．若DE的长度为30m，则A、B两地的距离为　60　m．

应用题．

根据三角形中位线求出AB=2DE，代入求出即可．

∵D、E分别是AC、BC的中点，DE=30m，

∴AB=2DE=60m

60．

本题考查了三角形的中位线的应用，注意：

三角形的中位线平行于第三边，并且等于第三边的一半．

4．（•广州,第11题3分）

中，已知

，则

的外角的度数是_____．

【考点】三角形外角

【分析】本题主要考察三角形外角的计算，

的外角为

【答案】

5．（•广州,第12题3分）已知

是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为点

，则PE的长度为_____．

【考点】角平线的性质

【分析】角平分线上的点到角的两边距离相等．

【答案】10

6.（•福建泉州，第15题4分）如图，在△ABC中，∠C=40°

，CA=CB，则△ABC的外角∠ABD=　110　°

等腰三角形的性质．

先根据等腰三角形的性质和三角形的内角和定理求出∠A，再根据三角形的外角等于等于与它不相邻的两个内角的和，进行计算即可．

∵CA=CB，

∴∠A=∠ABC，

∵∠C=40°

∴∠A=70°

∴∠ABD=∠A+∠C=110°

110．

此题考查了等腰三角形的性质，用到的知识点是等腰三角形的性质、三角形的外角等于等于与它不相邻的两个内角的和．

7.（•扬州，第10题，3分）若等腰三角形的两条边长分别为7cm和14cm，则它的周长为　35　cm．

题目给出等腰三角形有两条边长为7cm和14cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．

①14cm为腰，7cm为底，此时周长为14+14+7=35cm；

②14cm为底，7cm为腰，则两边和等于第三边无法构成三角形，故舍去．

故其周长是35cm．

故答案为35．

此题主要考查学生对等腰三角形的性质及三角形的三边关系的掌握情况．已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．

8.（•扬州，第15题，3分）如图，以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E，连结OD、OE，若∠A=65°

，则∠DOE=　50°

　．

（第2题图）

圆的认识；

三角形内角和定理；

首先根据三角形内角和求得∠B+∠C的度数，然后求得其二倍，然后利用三角形的内角和求得∠BOD+∠EOC，然后利用平角的性质求得即可．

∵∠A=65°

∴∠B+∠C=180°

﹣65°

=115°

∴∠BDO=∠DBO，∠OEC=∠OCE，

∴∠BDO+∠DBO+∠OEC+∠OCE=2×

115°

=230°

∴∠BOD+∠EOC=2×

180°

﹣230°

=130°

∴∠DOE=180°

﹣130°

=50°

本题考查了圆的认识及三角形的内角和定理等知识，难度不大．

9.（•乐山，第14题3分）如图，在△ABC中，BC边的中垂线交BC于D，交AB于E．若CE平分∠ACB，∠B=40°

，则∠A=　60　度．

线段垂直平分线的性质．.

根据线段垂直平分线得出BE=CE，推出∠B=∠BCE=40°

，求出∠ACB=2∠BCE=80°

，代入∠A=180°

﹣∠B﹣∠ACB求出即可．

∵DE是线段BC的垂直平分线，

∴BE=CE，

∴∠B=∠BCE=40°

∵CE平分∠ACB，

∴∠ACB=2∠BCE=80°

∴∠A=180°

﹣∠B﹣∠ACB=60°

本题考查了等腰三角形性质，线段垂直平分线性质，三角形内角和定理的应用，注意：

线段垂直平分线上的点到线段两个端点的距离相等．

10．（•四川成都,第12题4分）如图，为估计池塘岸边A，B两点间的距离，在池塘的一侧选取点O，分别取OA，OB的中点M，N，测得MN=32m，则A，B两点间的距离是　64　m．

根据M、N是OA、OB的中点，即MN是△OAB的中位线，根据三角形的中位线定理：

三角形的中位线平行于第三边且等于第三边的一半，即可求解．

∵M、N是OA、OB的中点，即MN是△OAB的中位线，

∴MN=

AB，

∴AB=2CD=2×

32=64（m）．

故答案是：

64．

本题考查了三角形的中位线定理应用，正确理解定理是解题的关键．

11．（•随州，第13题3分）将一副直角三角板如图放置，使含30°

角的三角板的直角边和含45°

角的三角板的一条直角边重合，则∠1的度数为　75　度．

平行线的性质

计算题；

压轴题．

根据三角形三内角之和等于180°

求解．

如图．

∵∠3=60°

，∠4=45°

∴∠1=∠5=180°

﹣∠3﹣∠4=75°

75．

考查三角形内角之和等于180°

12、（•宁夏，第16题3分）如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面的半径是　

三角形的外接圆与外心

网格型．

根据题意得出△ABC的外接圆的圆心位置，进而利用勾股定理得出能够完全覆盖这个三角形的最小圆面的半径．

如图所示：

点O为△ABC外接圆圆心，则AO为外接圆半径，

故能够完全覆盖这个三角形的最小圆面的半径是：

此题主要考查了三角形的外接圆与外心，得出外接圆圆心位置是解题关键．

三.解答题

1.（•益阳，第15题，6分）如图，EF∥BC，AC平分∠BAF，∠B=80°

．求∠C的度数．

（第1题图）

平行线的性质．

根据两直线平行，同旁内角互补求出∠BAF，再根据角平分线的定义求出∠CAF，然后根据两直线平行，内错角相等解答．

∵EF∥BC，

∴∠BAF=180°

﹣∠B=100°

∵AC平分∠BAF，

∴∠CAF=

∠BAF=50°

∴∠C=∠CAF=50°

本题考查了平行线的性质，角平分线的定义，熟记性质并准确识图是解题的关键．

2.　（•无锡，第22题8分）如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．

（1）若∠B=70°

，求∠CAD的度数；

（2）若AB=4，AC=3，求DE的长．

圆周角定理；

（1）根据圆周角定理可得∠ACB=90°

，则∠CAB的度数即可求得，在等腰△AOD中，根据等边对等角求得∠DAO的度数，则∠CAD即可求得；

（2）易证OE是△ABC的中位线，利用中位线定理求得OE的长，则DE即可求得．

（1）∵AB是半圆O的直径，

∴∠ACB=90°

又∵OD∥BC，

∴∠AEO=90°

，即OE⊥AC，∠CAB=90°

﹣∠B=90°

=20°

∵OA=OD，

∴∠DAO=∠ADO=

=55°

∴∠CAD=∠DAO﹣∠CAB=55°

﹣20°

；

（2）在直角△ABC中，BC=

∵OE⊥AC，

∴AE=EC，

又∵OA=OB，

∴OE=

BC=

又∵OD=

AB=2，

∴DE=OD﹣OE=2﹣

本题考查了圆周角定理以及三角形的中位线定理，正确证明OE是△ABC的中位线是关键．