离散数学模拟试题及答案Word格式.docx

离散数学模拟试题及答案Word格式.docx

《离散数学模拟试题及答案Word格式.docx》由会员分享，可在线阅读，更多相关《离散数学模拟试题及答案Word格式.docx（5页珍藏版）》请在冰豆网上搜索。

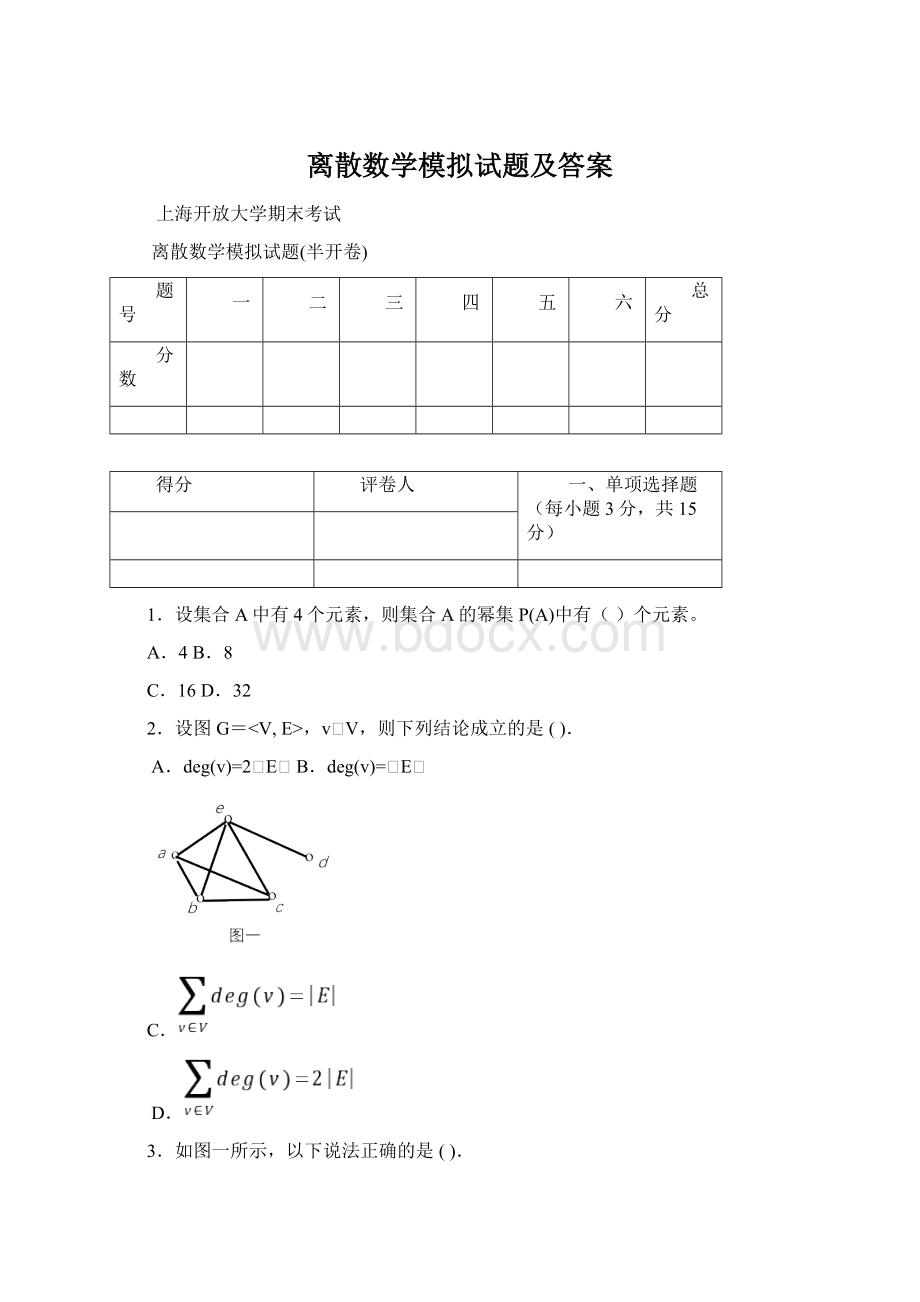
A．4B．8

C．16D．32

2．设图G＝<

V,E>

，vÎ

V，则下列结论成立的是（）．

A．deg（v）=2½

E½

B．deg（v）=½

C．

D．

3．如图一所示，以下说法正确的是（）．

A．（e,c）是割边B．（d,e）是割边

C．（b,a）是割边D．（b,c）是割边

4．命题公式P∨Q的合取范式是（）．

A．PB．P∧Q

C．P∨PD．P∨Q

5．下列公式中（）为永真式．

A．Ø

AÙ

Ø

B«

Ø

AÚ

BB．Ø

（AÚ

B）

C．Ø

AÚ

BD．Ø

（AÙ

B）

二、填空题（每小题3分，共15分）

1.命题公式PÚ

P的真值为．

2．设集合A={2,3,4}，B={1,2,3,4}，R是A到B的二元关系，

则R的有序对集合为　　　　　　．

3．设集合A={1，2}上的关系R＝{<

1,1>

<

1,2>

}，则在R中仅需加一个元素，就可使新得到的关系为对称的．

4．设G是具有n个结点m条边k个面的连通平面图，则m等于．

5．若无向树T有5个结点，则T的边数为．

三、逻辑公式翻译题（每小题6分，共18分）

1．将语句“今天上班”翻译成命题公式．

2．将语句“他去操场锻炼，仅当他有时间”翻译成命题公式．

3.将语句“所有的人都要呼吸”翻译成谓词公式．

四、判断说明题（每小题5分，共10分）

1．如果图G是无向图，且其结点度数均为偶数，则图G是欧拉图．

2.函数f:

N→N,f（x）=2x,其中N为自然数集，则f是双射的。

五、计算题（每小题12分，共36分）

1．设集合A={{1},1,2}，B={1,{1,2}}，试计算

（1）AB；

（2）A∩B；

（3）A×

B．

2．画一棵带权为1,2,2,3,4的最优二叉树,计算它们的权．

3．求（P∨Q）→（R∨Q）的合取范式．

六、证明题（本题6分）

试证明：

若R与S是集合A上的对称关系，则R∩S也是集合A上的对称关系．

离散数学模拟试题答案

一、选择题（每小题3分，共15分）

1.C2．D3．B4．D5．B

二、填空题（每小题3分，共15分）

1.1或真2．{<

2,2>

，<

2,3>

2,4>

3,3>

}，<

3,4>

4,4>

}

3．<

2,1>

4．n+k-25．4

三、逻辑公式翻译题（每小题6分，共18分）

1．设P：

今天上班，

则命题公式为：

P．

2．设P：

他去操场锻炼，Q：

他有时间，

则命题公式为：

P®

Q．

3.设P（x）：

x是人，Q（x）：

x要呼吸，

则谓词公式为：

x（P（x）→Q（x））

四、判断说明题（每小题5分，共10分）

1．错误．

当图G不连通时图G不为欧拉图．

2．错误．

f是单射的，但不是满射的,因为ranfN,因为ranf不含有奇数.

五、计算题（每小题12分，共36分）

解：

1．

（1）AB={{1},2}

（2）A∩B={1}

（3）A×

B={<

{1},1>

{1},{1,2}>

1,1>

1,{1,2}>

2,1>

2,{1,2}>

}

2．

权为13+23+22+32+42=27

3．（P∨Q）→（R∨Q）

Û

（P∨Q）∨（R∨Q）

（Ø

P∧Ø

Q）∨（R∨Q）

P∨R∨Q）∧（Ø

Q∨R∨Q）

Û

P∨R∨Q）∧1

P∨R∨Q）（合取范式）

证明：

设x，yA，因为R对称，所以若<

x,y>

R，则<

y,x>

R．

因为S对称，所以若<

S，则<

S．

于是若<

R∩S则<

R且<

S

即<

也即<

R∩S，故R∩S是对称的．