矩阵的概念和线性运算Word下载.docx
《矩阵的概念和线性运算Word下载.docx》由会员分享,可在线阅读,更多相关《矩阵的概念和线性运算Word下载.docx(22页珍藏版)》请在冰豆网上搜索。
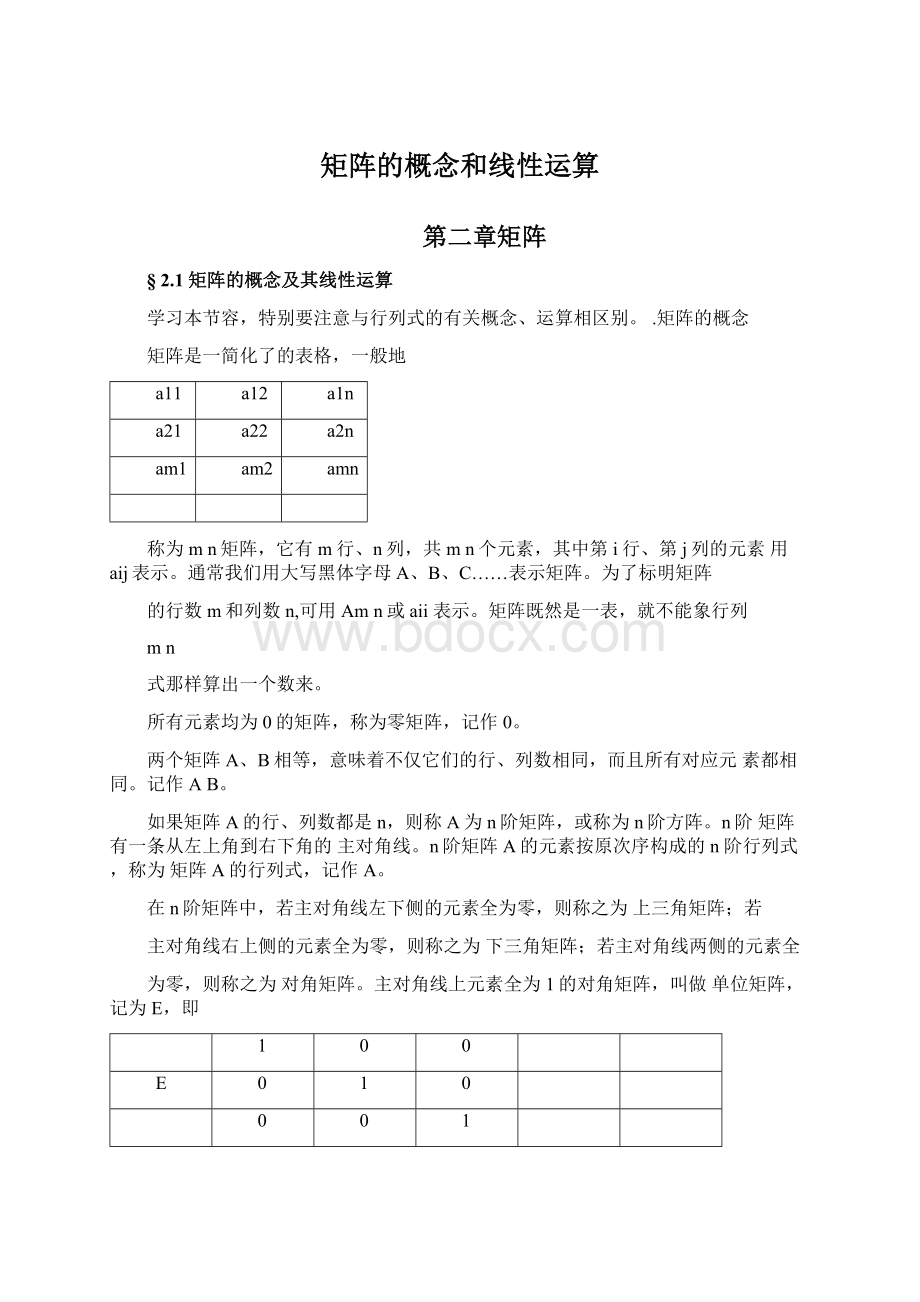
AB、AB。
分别称为矩阵A、B的和与差。
AB表示将A、B中所有对应位置的元素相加、减得到的矩阵。
例如
2
3
4
A
5
B
32
35
3(
3)
20
50
11
62
三.矩阵的数乘
矩阵
A与数k相乘记为
kA或Ak0kA表示将
k乘A中的所有兀素得到的矩
3234
6
12
0,3A
3330
9
3531
15
当k1时,我们简记
(1)AA,称为A的负矩阵。
矩阵的加减与数乘统称为线性运算。
不难验证线性运算满足交换律、结合律与分配律,这与数量的运算规律相同,所以在数量运算中形成的诸如提取公因子、合并同类项、移项变号、正负抵消等运算习惯,在矩阵的线性运算中都可以保留、沿用。
31
7
例
2.1设A
15
79,B
7,已知
24
68
A2X
B,求Xo
解
2XB
再除以2
得
1/
A)。
通过心
在等式中移项得
X
-(B
算立得
X2
121721
例2.2设A为三阶矩阵。
已知A2,求行列式3A的值。
a1
a2
a3
3a1
3a2
3a3
解设A
b1
b2
b3,则3A
3b1
3b2
3b3
C1
C2
C3
3c1
3c2
3c3
显然行列式3A中每行都有公因子3,因此
2.2矩阵的乘法与转置
.矩阵的乘法
如果矩阵A的列数与矩阵B的行数相同,即A是ms矩阵,B是sn矩阵,那么A、B可以相乘,记为AB或AB,称为矩阵A、B的乘积。
ABC表示一个mn矩阵,矩阵C的构成规则如下:
B的第1列元素依次与A的各行元素相组合,形成C的第1列元素;
B的第2列元素依次与A的各行元素相组合,形成C的第2列元素;
……以此类推,最后B的第n列元素依次与A的各行元素相组合,形成C的第n列元素。
这里的“组合”表示两两相乘再相加。
的元素可用公式表示为
s
(2.1)
Cijaikbkj(i=l,2,…,m;
j=1,2,…,n)
k1
03123
14210
21
(2.2)
(1)
3
(2)
(1)1
1)
(2)
41
利用矩阵的乘法可以简化线性方程组的表示形式。
设
am1X1am2X2amnXn
是含有m个方程、n个变量的线性方程组,若记
a1n
X1
X
X2
b
Xn
bm
则方程组可表示为矩阵方程
Axb(2.3)
这个矩阵方程两端都是m1矩阵,因此相当于m个等式,恰好是(2.2)
式的m个方程。
(2.3)式称为线性方程组(2.2)的矩阵形式。
以后,矩阵形式(2.3)
将成为我们表示线性方程组的主要形式。
其中A称为线性方程组的系数矩阵,x称为变量列,b称为常数列。
二•矩阵乘法的性质
两个矩阵相乘要求行、列数相匹配,即在乘积AB中,矩阵A的列数必须等于矩阵B的行数,因此当AB有意义时,BA未必有意义。
即使AB和BA都有意义,它们也可能表示不同阶数的矩阵。
比如A是1n矩阵(行向量),B是n1
矩阵(列向量)时,
AB是11矩阵而BA为nn矩阵。
当A、B都是n阶方
阵时,情况又怎样呢?
88
例2.3设A
B
C
,求AB、
12
36
04
BA、ACo
解利用乘积的构成规则容易得到
16
32
AB
8
00
BA
AC
从例2.3可以看到矩阵乘法的两个重要特点:
(1)矩阵乘法不满足交换律。
即一般情况下ABBAo
(2)矩阵乘法不满足消去律。
即从AO和ABAC不能推得BCo特别地,当BAO时,不能断定AO或者BOo
这两个特点与数量乘法的规律不同,所以在数量运算中形成的交换与消去习惯必须改变。
矩阵相乘时要注意顺序,有左乘、右乘之分。
不过,矩阵的自乘无需区别左乘右乘,因此,可以引入矩阵乘幕的记号,比如
AAAA3
这里A是n阶方阵。
方阵的乘幕显然有下列性质
AkA1Ak1,(Ak)1Akl
其中k、1是自然数。
但是因为A、B的乘积不能交换顺序,所以
222
(AB)(AB)(AB)(AA)(BB)AB
一般情况下,
当k
2时,
(AB)
k
AkB
o
这与数量的乘幕运算规则大不相同
例2.4
设A
,求P(A)
2A23A
4E
解P(A)
3A4E
29
14
13
30
10
01
本例中,P(A)与多项式P(x)2x3x4有类似的形式,因此称它为矩阵多项式。
一般地,如果一个矩阵式的每一项都是带系数的同一方阵A的非负整
数幕,“常数项”(零次幕项)是带系数的单位矩阵,那么称这个矩阵式为关于A
的矩阵多项式。
如果矩阵A、B满足ABBA,那么称A、B是可交换的。
可交换是个很强的条件,下面介绍两种特殊情况。
一种是对角矩阵。
容易验证
a
0L
L
aa
a2L
(2.4)
LL
an
bn
anbn
交换乘积的顺序,结果显然相冋。
由此可知
:
两个冋阶对角矩阵是可交换的,它
们的乘积矩阵由对应位置元素的乘积构成。
另一种是单位矩阵。
设Aaijmn,Em、En分别为m阶、n阶单位矩阵,
不难验证EmAA,AEnA。
特别地,当mn时
EAAEA(2.5)
可见单位矩阵E在矩阵乘法中与数1在数量乘法中有类似的作用。
单位矩阵与任何同阶矩阵可交换。
矩阵的乘法虽然不满足交换律,但仍满足下列运算规律(假设运算都是可行
的):
(1)乘法结合律:
(AB)CA(BC)
(2)左、右分配律:
(AB)CACBC,C(AB)CACB
(3)数乘结合律:
k(AB)(kA)BA(kB)
这些运算律的证明,都可以利用乘法公式(2.1)以及通过和式的乘积展开与
重组来完成,此处从略。
这些运算律与数量的运算规律相同,所以在数量运算中形成的诸如多项乘积展开、系数归并化简、因式分解、连乘重组等运算习惯,在矩阵的运算中,仍可保留沿用,当然应该特别注意不可随意交换乘法顺序,不可随意约简非零因子。
三•矩阵的转置
把矩阵A的行与列互换所得到的矩阵称为矩阵A的转置矩阵,记为At,即
T
A
矩阵的转置方法与行列式相类似,但是矩阵转置后,行、列数都变了,各元素的位置也变了,所以通常AAt。
转置矩阵有如下性质(其中
A、
B是矩阵,
k是数):
(1)(AT)T
(AB)T
atbt
(3)(kA)T
kAT
(4)
(ab)t
btat
这里性质
(1)
~(3)是显然的,
性质(4)
可利用乘法公式(2.1)证明
201
例2.5设Ai32,计算AAT和"
A。
aat
ata
若方阵A满足AA,则称A为对称矩阵。
比如例2.5所求的两个矩阵都是对称矩阵。
四•方阵行列式的乘积定理
设A、B都是n阶方阵。
一般地ABBA,但它们的行列式相等,并且
ABBAAB(2.6)
定理2.1方阵乘积的行列式等于各因子行列式的乘积。
这个定理的结论简明、自然,但它的证明很复杂,并且需要用到特殊的构造性技巧,此处从略。
2.3逆矩阵
一.逆矩阵的概念
设A是n阶矩阵(方阵),如果存在n阶矩阵B,使得ABBAE,则称矩阵A是可逆的,并称B是A的逆矩阵。
矩阵A可逆时,逆矩阵B必唯一。
事实上,若另有一逆矩阵B,,则由ABE和B1AE得到B,B,EB,(AB)(B,A)B
EBB。
这样,逆矩阵可以有唯一的记号。
记A的逆矩阵为A1,即
AA1A1AE
(2.7)
比如不难验证
A1
13
逆矩阵相当于矩阵的
~T—、,fA
倒数
但是因为矩P牛的乘法有左乘、
右乘之分,所以
不允许以分数线表示逆矩阵。
如果三个矩阵A、
B、
C满足AB
AC,
且A可逆,
那么在等式两边左
乘逆矩阵A二可得A
1AB
1AC,
即EB
EC
,从而B
C。
这说明利
用逆矩阵可以实现“约简”,换言之,矩阵的乘法并非没有消去规则,但消去规则
必须通过逆矩阵的乘法来实现,可逆才有消去律。
当然,在等式两边乘逆矩阵时应当注意分清左乘还是右乘。
逆矩阵为求解矩阵方程带来了方便。
比如线性方程组Axb中,若A可逆,
Ab,事先求出逆矩阵
C中,
则x
又如矩阵方程AXB
XACBo
A,只要做一次乘法,
若A、
B均可逆,
即可求得所有变量的值。
则未知矩阵直接可求:
.矩阵可逆的条件设有n阶方阵
an1
an2
ann
它的行列式A有n个代数余子式得到矩阵
Aj
(i,j=1,2,••
n),将它们按转置排列,
称A为矩阵验证
AA
如果A
A1
.*AI2
An
A21
A22
A2n
An1
An2
Ann
A的伴随矩阵。
利用第一章的定理1.2(代数余子式组合定理)
容易
0AE
0,则上式两端除以非零数
A,可得
AjqA
Aa*ae
这说明矩阵A可逆,并且
丄A*
(2.8)
定理2.2方阵A可逆的充分必要条件是它的行列式不等于零:
证(2.8)式已给出充分性证明,现证必要性。
如果矩阵
AA1E取行列式,根据定理2.1的(2.6)式得A1
因而必有A0o
行列式非零的方阵又叫做非奇异矩阵。
显然,非奇异矩阵和可逆矩阵是等价的概念。
行列式等于零的矩阵自然叫做奇异矩阵。
奇异矩阵即不可逆矩阵有无数多个,这与数量中唯有数
0没有倒数大不相同。
例2.6设A
2,求A1o
解显然A
A可逆,
AA1
0。
则由
0,A的代数余子式都是一阶行列式,不需要计算,只
要附上适当的符号,并注意转置排列即可:
142
"
231
公式(2.8)给出了求逆矩阵的方法,但是求伴随矩阵A要计算n2个(n1)
阶行列式,当n较大时,计算量非常大。
我们将在下一节介绍更好的方法。
定理2.3设A、B都是n阶矩阵,则BA的充分必要条件是ABE或者BAE。
证必要性显然,只证充分性。
若ABE,取行列式得AB1,故
A0,则根据定理2.2,A存在。
等式两端左乘A,立得111
BAABAEA。
BAE的情况相同,证毕。
定理2.3表明,检验或者证明B是否A的逆矩阵,只要做一个乘法即可。
比
如从公式(
2.4)
很容易求得对角矩阵的逆矩阵。
印
1a1
1a2
(2.9)
1an
其中a1a2
三•逆矩阵的性质
(1)若A可逆,则A1也可逆,且(A1A。
证根据定理(2.3),只需做一个乘法:
因为AA1E,故得证。
(2)若A可逆,则AT也可逆,且(AT)1(A1)T。
证因为At(A1)t(A1A)tEtE,故得证。
(3)若A、B是同阶矩阵且都可逆,则(AB)1B1A1。
证因为(AB)(B1A1)A(BB1)A1AEA1AA1E,故得证。
2.4矩阵的初等变换
一•矩阵的初等行变换
在第一章中,我们已经看到了行(列)变换在行列式计算中的重要作用。
对矩阵也有类似的变换。
对矩阵施行下列三种变换,统称为矩阵的初等行变换:
(1)换行变换:
将矩阵的两行互换位置。
(2)倍缩变换:
以非零数k乘矩阵某一行的所有元素。
(3)消去变换:
把矩阵某一行所有元素乘同一数k加到另一行对应的元素上去。
例如对下列矩阵
车作初等行
变换:
先将第
3行乘
2加t
到第1行,再将第1、3
行互换,得到0
由于矩阵的初等变换改变了矩阵的元素,因此初等变换前后的矩阵是不相等的,应该用“”连接而不可用“=”连接。
矩阵的初等变换可以链锁式地反复进行,以便达到简化矩阵的目的。
类似地可引入初等列变换的概念。
.初等变换的标准程序
3,求A1。
例2.7已知A
解将矩阵A和单位矩阵E拼成一个36矩阵AE。
类似于行列式的
降阶变换(参看
■§
1.2),对
E施行
系列初等行变换:
AE
[1]
[4]1
14
34
74
52
7,4
1.2
可以验证,最后的矩阵中,右侧的矩阵就是逆矩阵,即
A134
1.4
本例的结果不是偶然的。
在论证这一方法之前,我们先结合例2.7介绍矩阵
初等变换的标准程序:
(1)变换分步进行,每步选一非零元素,称为主元。
利用行倍缩变换把主
元变为1,并且通过行消去变换把主元所在列的其它元素全都变为0。
(2)所选的主元必须位于不同的行。
逐步重复上述变换,直至选不出新的主元为止。
(3)穿插换行变换,使主元呈左上到右下排列。
简单地说,标准程序就是通过初等行变换(不允许做列变换),变出一个一
个不同的基本单位列,直至变不出新的基本单位列为止。
基本单位列是指一个元
素为1其余元素全都为0的列向量。
比如在例2.7的运算中,带“*”号的第二步是以元素1为主元,将第2行乘1和2分别加到第1、3行上去;
最后一步(第四步)并未选主元,而是作了一个互换第1、3行的换行变换。
在所有的行消去变换中,主元都用“[]”号作了标
记。
标准程序体现了初等变换的目的性和条理性。
矩阵的初等变换将贯穿本书的始终,初等变换的标准程序也将反复多次得到应用。
三•用初等变换法求逆矩阵
设A是n阶矩阵,E是n阶单位矩阵,对n2n矩阵AE按标准程序作初等行变换,主元在左半部分(即前n列)的围选取。
当把子块A变成单位矩阵
E的同时,右半部分必然变成了A(参看例2.7)o
例2.8设A4
6,
问A
是否存在?
解运用初等变换法
AE4
60
0[
3]
90
53
230
43
130
标准程序已执行完毕,但子块A未变成单,
位矩阵,即
卩在未
选主元1
的行中没有非零
元素,无法选出新的主元,此时可以断定A不可逆。
其理由如下:
设想对行列式A施行初等变换。
如果将换行变换、倍缩变换或消去变换施加于行列式,则行列式的值仅仅是改变符号、非零倍缩或保持不变,总之初等变换不改变行列式的非零性,因此能通过初等变换检验矩阵的可逆性(参看定理2.2)o
例2.8说明用初等变换法求逆矩阵,不必事先知道矩阵是否可逆。
四•初等矩阵
对单位矩阵E施行一次初等变换得到的矩阵称为初等矩阵。
例如下面三个矩
阵
02