新人教版数学八年级上册第十三章第11课时 最短路径问题教师版Word文档下载推荐.docx

新人教版数学八年级上册第十三章第11课时 最短路径问题教师版Word文档下载推荐.docx

《新人教版数学八年级上册第十三章第11课时 最短路径问题教师版Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《新人教版数学八年级上册第十三章第11课时 最短路径问题教师版Word文档下载推荐.docx（16页珍藏版）》请在冰豆网上搜索。

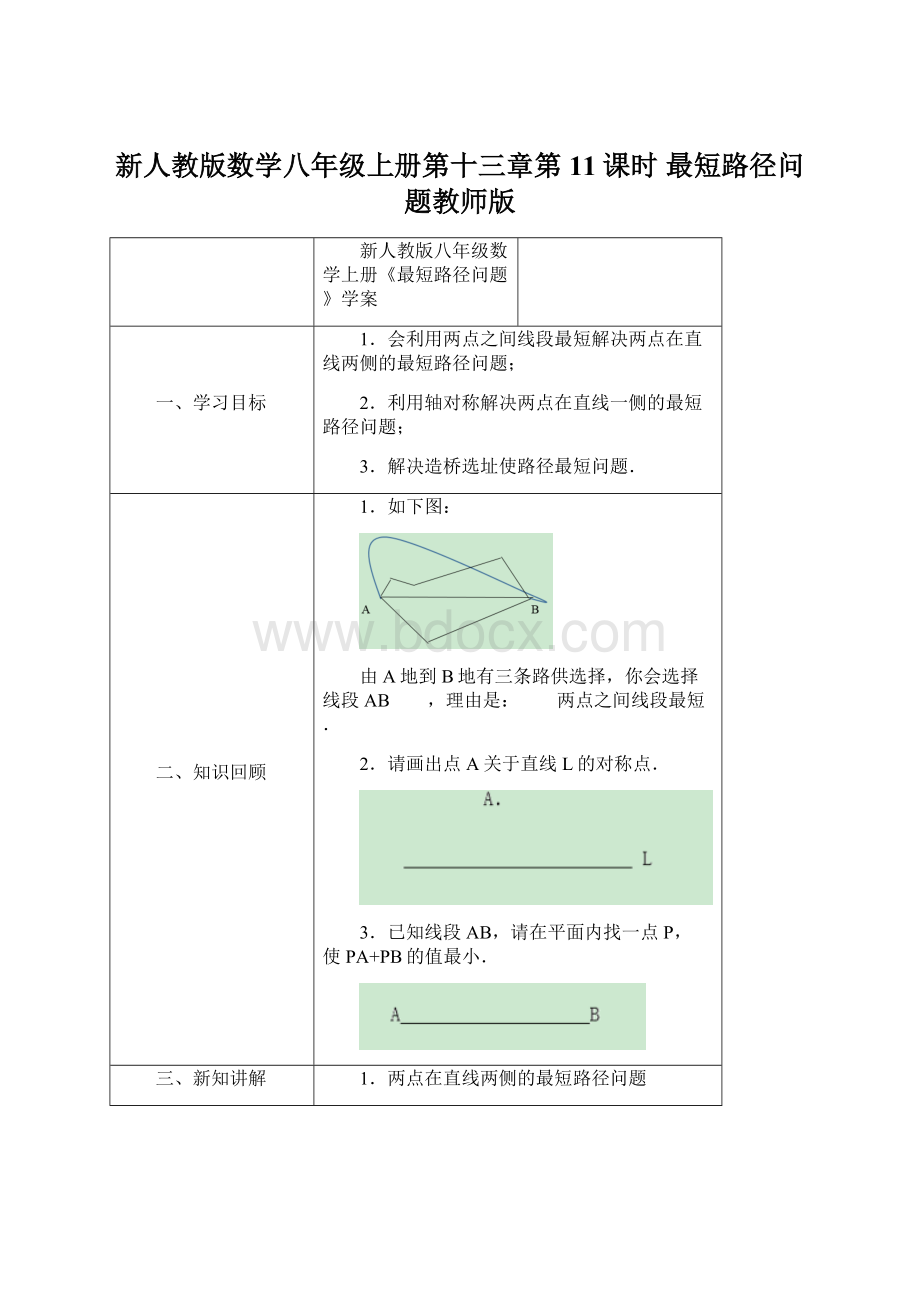
证明：

由作图可知，点B和B′关于直线l对称，

∴直线l是线段BB′的垂直平分线．

∵点C与C′在直线l上，

∴BC＝B′C，BC′＝B′

C′.

在△AB′C′中，AB′＜AC′＋B′C′，

∴AC＋B′C＜AC′＋B′C′，

故AC＋BC＜AC′＋C′B.

3．最短路径选址问题

解决连接河两岸

的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．

四、典例探究

扫一扫，有惊喜哦！

【例1】如图所示，点A，B分别是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短．

作法：

连接AB与l交于一点C，这时CA+CB最短．

理由是：

总结：

当两点在直线两侧，求直线上一点与这两点的距离和最短时，可以连接这两点，这两点的连线与直线的交点即为所求.其依据是：

两点之间，线段最短．

练1如图所示，工厂A与工厂B想在公路m旁修建一座共用的仓库O，并且要求O到A与O到B的距离之和最短，请你在m上确定仓库应修建的O的位置，同时说明你选择该点的理由．

【例2】

（2014秋•安阳期末）如图，已知△ABC是等边三角形，D、E分别是AB、AC边上的点，且DB=EC．

（1）画图：

在BC边上找一点P，使点P到点D、点E的距离的和最短（简要说明

画法，保留画图痕迹）．

（2）在

（1）的条件下，证明PB=PC．

当两点在直线同侧，求直线上一点与这两点距离和最短时，把两点在直线同侧问题转化为两点在直线两侧问题，再求解.

练2（2014秋•丹阳市校级期末）如图，正方形ABCD的面积为36，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）

A．5B．6C．7D．8

【例3】如图，从A地到B地经过一条小河（河岸平行），今欲在河上建一座与两岸垂直的桥，应如何选择桥的位置才能使从A地到B地的路程最短？

在解决造桥选址问题时，通常利用平移变换，把已知问题转化成容易解决的问题，从而作出最短路径.

练3如图，如果A、B两地之间有两条平行的河，我们要建的桥都是与河岸垂直的．我们如何找到这个最短的距离呢？

五、课后小测

一、选择题

1．（2014秋•黔东南州期末）如图，直线l是一条河，A、B两地相距10km，A、B两地到l的距离分别为8km、14km，欲在l上的某点M处修建一个水泵站，向A、B两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（）

A．

B．

C．

D．

2．（2013秋•合浦县期末）如图所示，四边形OABC为正方形，边长为3，点A，C分别在x轴，y轴的正半轴上，点D在OA上，且D的坐标为（1，0），P是OB上的一动点，则“求PD+PA和的最小值”要用到的数理依据是（）

A．“两点之间，线段最短”

B．“轴对称的性质”

C．“两点之间，线段最短”以及“轴对称的性质”

D．以上答案都不正确

3．（2014秋•青山区期中）已知点A（﹣2，1），点B（3，2），在x轴上求一点P，使AP+BP最小，下列作法正确的是（）

A．点P与O（0.0）重合

B．连接AB交y轴于P，点P即为所求．

C．过点A作x轴的垂线，垂足为P，点P即为所求

D．作点B关于x轴的对称点C，连接AC，交x轴于P，点P即为所求

4．（2014秋•梁子湖区期末）如图，在四边形ABCD中，∠DAB=130°

，∠D=∠B=90°

，点M，N分别是CD，BC上两个动点，当△AMN的周长最小时，∠AMN+∠ANM的度数为（）

A．90°

B．100°

C．130°

D．140°

二、填空题

5．（2015•许昌一模）如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是_____．

三、解答题

6．（2014•红塔区模拟）已知：

如图所示，

（1）作出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′三个顶点的坐标．

（2）在x轴上画出点P，使PA+PC最小．

7．（2014春•通川区校级期末）河的一旁有两个村子A、B，要在河边建一水泵站引水到村里．一村民画了一张图，以直线l表示一条河，在河的另一边作A的对称点C，连接BC得与l的交点P，那么P到A、B的距离和总比l上其它点到A、B的距离和短，你能说出其中的道理吗？

8．如图7，如果A、B之间有三条平行的河流，河流1和河流2上都要造桥，桥造在何处可使从A到B的路径最短？

典例探究答案：

【例1】两点之间，线段最短.

练1．【解析】根据两点之间线段最短，连接AB与直线m的交点即为所求．

解：

如图，连接AB交直线m于O，

则O点即为所求的点．

理由如下：

根据连接两点的所有线中，线段最短．

【例2】【解析】

（1）作点E关于直线BC的对称点E′，连接DE′，DE′与直线BC的交点P的位置即为所求．

（2）连接CE′，由对称轴的性质得EC=EC′，进而求得DB=E′C，然后根据AAS证得△PBD≌△PCE′，根据全等三角形对应边相等从而证得结论．

解；

（1）如图，作点E关于直线BC的对称点E′，连接DE′，DE′与直线BC的交点P的位置即为所求．

（2）连接CE′，由对称轴的性质得EC=EC′，

∵DB=EC，

∴DB=E′C，

∵△ABC是等边三角形，

∴∠B=∠ECB=∠E′CP=60°

，

在△PBD和△PCE′中，

∴△PBD≌△PCE′（AAS），

∴PB=PC．

点评：

本题考查的是轴对称及最短路线问题，三角形全等的判定和性质，涉及正三角形的性质、两点之间线段最短等知识．

练2．【解析】如图，由正方形的性质可以得出D点的对称点F与B点重合，EF=EP+DP，解一个直角三角形就可以求出结论．

如图，∵四边形ABCD是正方形，

∴AB=BC=CD=AD，BO=DO．AC⊥BD，

∴B、D关于AC对称，

∴PD=PB，

∴PD+PE=PB+PE=BE．

∵△ABE是等边三角形，

∴AB=BE=AE．

∵正方形ABCD的面积为36，

∴AB=6，

∴BE=6．

∴PD+PE的和最小值为6．

故选：

B．

本题考查了正方形的面积公式的运用，正方形的性质的运用，轴对称的性质的运用．最短路径问题的运用等边三角形的性质的运用，解答时正确作出图形找到对称点是关键．

【例3】【解析】从A到B要走的路线是A→M→N→B，如图所示，而MN是定值，于是要使路程最短，只要AM＋BN最短即可．此时两线段应在同一平行方向上，平移MN到AC，从C到B应是余下的路程，连接BC的线段即为最短的，此时不难说明点N即为建桥位置，MN即为所建的桥．

（1）如图，过点A作AC垂直于河岸，且使AC等于河宽．

（2

）连接BC与河岸的一边交于点N.

（3）过点N作河岸的垂线交另一条河岸于点

M.

则MN为所建的桥的位置．

练3．【解析】方法1：

可以将点A沿与河垂直的方向平移两个河宽分别到到A1、A2，路径中两座桥的长度是固定的．为了使路径最短，只要A2B最短．连接A2B，交河流2河岸于N，在此处造桥MN；

连接A1M，交河流1河岸于P，在此处造桥PQ．所得路径AQPMNB最短．

方法2：

此题还可以用以下方法来确定建桥位置．

如图6，将点A沿与第一条河流垂直的方向平移一个河宽到A1，将B沿与第二条河垂直的方向平移一个河宽到B1，连接A1B1与两条河分别相交于N、P，在N、P两处，分别建桥MN、PQ，所得路径AQPMNB最短．

课后小测答案：

1．【解析】作点A关于直线l的对称点，再把对称点与点B连接，根据轴对称确定最短路线问题，交点即为所求点M．

根据轴对称确定最短路线问题，B选项图形方案符合．

本题考查了轴对称确定最短路线问题，熟练掌握最短路线的确定方法是解题的关键．

2．【解析】先根据正方形的性质得出A、C两点关于直线OB对称，连接CD，则CD即为PD+PA和的最小值．

∵四边形OABC为正方形，

∴A、C两点关于直线OB对称（轴对称的性质），

∴连接CD，则CD即为PD+PA和的最小值（两点之间，线段最短），

∴用到的数理依据是“两点之间，线段最短”以及“轴对称的性质”．

本题考查的是轴对称﹣最短路线问题，熟知“两点之间，线段最短”以及“轴对称的性质”是解答此题的关键．

3．【解析】根据题意画出图形，根据图形即可判断．

如图作点A关于x轴的对称点A′，连接A′B交x轴于点P，则P点即为所求点．

D．

本题考查的是轴对称﹣最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．

4．【解析】作点A关于BC的对称点A′，关于CD的对称点A″，根据轴对称确定最短路线问题，连接A′A″与BC、CD的交点即为所求的点M、N，利用三角形的内角和定理列式求出∠A′+∠A″，再根据轴对称的性质和三角形的一个外角等于与它不相邻的两个内角的和可得∠AMN+∠ANM=2（∠A′+∠A″），然后计算即可得解．

如图，作点A关于BC的对称点A′，关于CD的对称点A″，

连接A′A″与BC、CD的交点即为所求的点M、N，

∵∠BAD=130°

，∠B=∠D=90°

∴∠A′+∠A″=180°

﹣∠130°

=50°

由轴对称的性质得：

∠A′=∠A′AM，∠A″=∠A″AN，

∴∠AMN+∠ANM=2（∠A′+∠A″）=2×

50°

=100°

．

本题考查了轴对称确定最短路线问题，轴对称的性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，确定出点M、N的位置是解题的关键，要注意整体思想的利用．

5．【解析】根据轴对称做最短路线得出AE=B′E，进而得出B′O=C′O，即可得出△ABC的周长最小时C点坐标．

作B点关于y轴对称点B′点，连接AB′，交y轴于点C′，

此时△ABC的周长最小，

∵点A、B的坐标分别为（1，4）和（3，0），

∴B′点坐标为：

（﹣3，0），AE=4，

则B′E=4，即B′E=AE，

∵C′O∥AE，

∴B′O=C′O=3，

∴点C′的坐标是（0，3），此时△ABC的周长最小．

故答案为（0，3）．

此题主要考查了利用轴对称求最短路线以及平行线的性质，根据已知得出C点位置是解题关键．

6．【解析】

（1）根据轴对称的性质分别作出A、B、C三点关于y轴的对称点A′、B′、C′，分别连接各点即可；

（2）先找出C先找出C点关于x轴对称的点C″（4，﹣3），连接C″A交x轴于点P，则点p即为所求点．

（1）

分别作A、B、C的对称点，A′、B′、C′，由三点的位置可知：

A′（﹣1，2），B′（﹣3，1），C′（﹣4，3）

（2）先找出C点关于x轴对称的点C″（4，﹣3），连接C″A交x轴于点P，

（或找出A点关于x轴对称的点A″（1，﹣2），连接A″C交x轴于点P）则P点即为所求点．

本题考查的是最短路线问题及轴对称的性质，解答此题的关键是熟知两点之间线段最短的知识．

7．【解析】根据轴对称的性质，三角形三边关系定理判定线段的大小．

在直线l上任取一点Q，连接AQ、BQ，

∵A、C两点关于直线l轴对称，

∴AP=PC，AQ=CQ，CP+PB=BC，

又在△BCQ中，由三边关系定理，得BQ+CQ＞BC，

即BQ+AQ＞CP+BP，

∴BQ+CQ＞AP+BP．

本题考查了三角形三边关系和最短线路问题．解题的关键是根据“三角形两边之和大于第三边”，判断AP+BP最小．

8．【解析】方法1：

将点A沿与河垂直的方向平移S三个河宽分别到到A1、A2、A3，路径中三座桥的长度是固定的．为了使路径最短，只要A3B最短．

连接A3B，交河流3于N，在此处造桥MN；

连接A2N，交河流2于P，在此处造桥PQ；

连接A1Q，交河流1于R，在此处造桥RS．所得路径ASRQPMNB最短．

此处还可以先将A沿与河流1河岸垂直的方向平移两个单位到A1、A2，再将B沿与河流3河岸垂直的方向平移一个河宽到B1；

或先将A沿与河岸垂直的方向平移1个单位到A1，再将B沿与河岸平移2一个河宽到B1、B2，来选择修桥位置．