高考数学 考点单元复习教案文档格式.docx

高考数学 考点单元复习教案文档格式.docx

《高考数学 考点单元复习教案文档格式.docx》由会员分享，可在线阅读，更多相关《高考数学 考点单元复习教案文档格式.docx（32页珍藏版）》请在冰豆网上搜索。

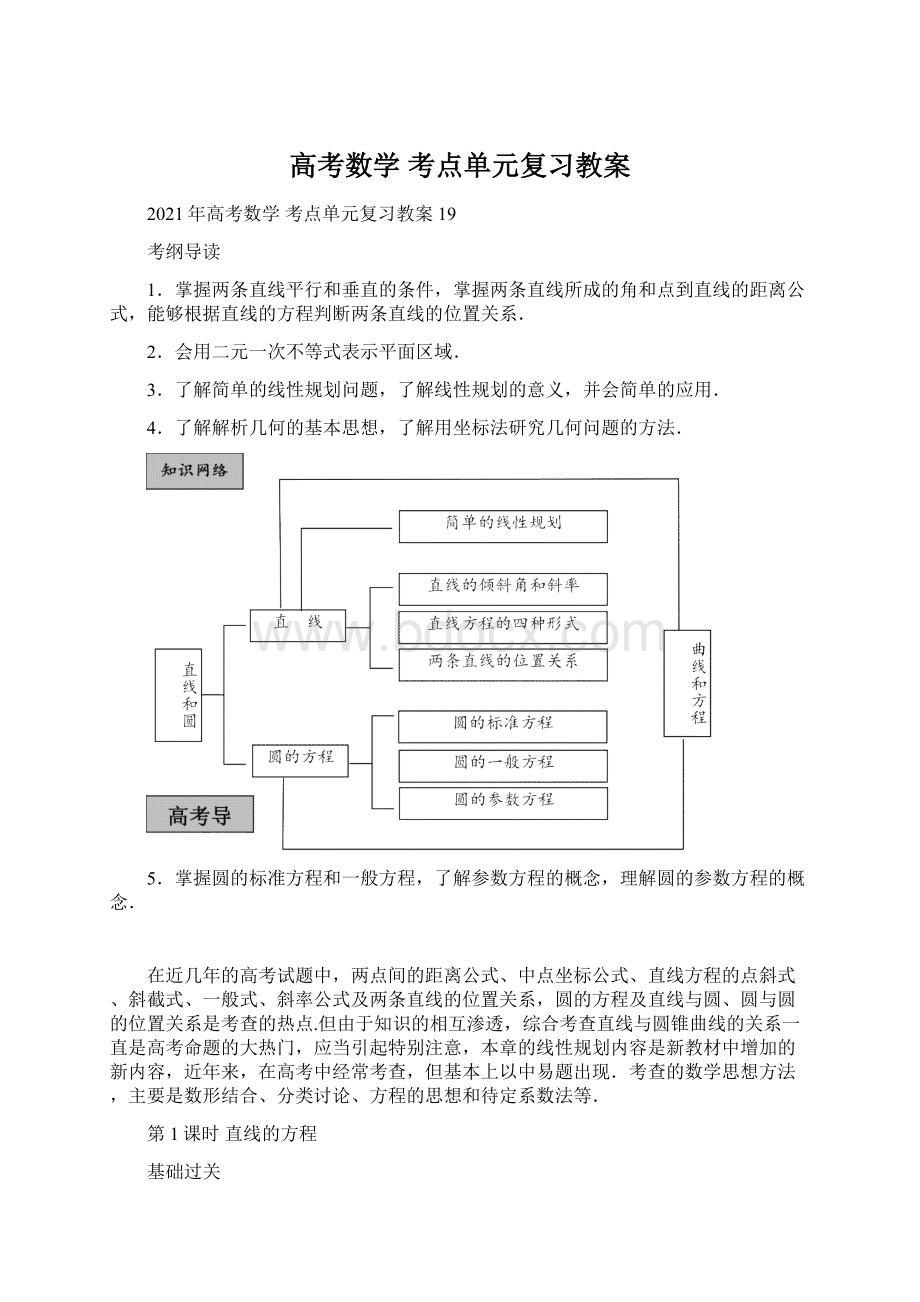
（2）设直线的斜率k=2，P1（3，5），P2（x2，7），P（－1，y3）是直线上的三点，则x2，y3依次是（）

A．－3，4B．2，－3C．4，－3D．4，3

（3）直线l1与l2关于x轴对称，l1的斜率是－

，则l2的斜率是（）

A．

B．－C．D．－

（4）直线l经过两点（1，－2），（－3，4），则该直线的方程是．

（1）D．提示：

直线的斜率即倾斜角的正切值是－．

（2）C．提示：

用斜率计算公式．

（3）A．提示：

两直线的斜率互为相反数．

（4）2y＋3x＋1=0．提示：

用直线方程的两点式或点斜式.

例2.已知三点A（1，-1），B（3，3），C（4，5）.

求证：

A、B、C三点在同一条直线上.

证明方法一∵A（1，-1），B（3，3），C（4，5），

∴kAB==2,kBC==2，∴kAB=kBC，

∴A、B、C三点共线.

方法二∵A（1，-1），B（3，3），C（4，5），

∴|AB|=2，|BC|=，|AC|=3，

∴|AB|+|BC|=|AC|，即A、B、C三点共线.

方法三∵A（1，-1），B（3，3），C（4，5），

∴=（2，4），=（1，2），∴=2.

又∵与有公共点B，∴A、B、C三点共线.

变式训练2.设a，b，c是互不相等的三个实数，如果A（a，a3）、B（b，b3）、C（c，c3）在同一直线上，求证：

a+b+c=0.

证明∵A、B、C三点共线，∴kAB=kAC，

∴，化简得a2+ab+b2=a2+ac+c2，

∴b2-c2+ab-ac=0，（b-c）（a+b+c）=0，

∵a、b、c互不相等，∴b-c≠0，∴a+b+c=0.

例3.已知实数x,y满足y=x2-2x+2（-1≤x≤1）.

试求：

的最大值与最小值.

由的几何意义可知，它表示经过定点P（-2，-3）与曲线段AB上任一点（x,y）的直线的斜率k,如图可知：

kPA≤k≤kPB,

由已知可得：

A（1，1），B（-1，5），

∴≤k≤8，

故的最大值为8，最小值为.

变式训练3.若实数x,y满足等式（x-2）2+y2=3，那么的最大值为（）

A.B.C.D.

答案D

例4.已知定点P（6,4）与直线l1:

y＝4x，过点P的直线l与l1交于第一象限的Q点，与x轴正半轴交于点M．求使△OQM面积最小的直线l的方程．

Q点在l1:

y＝4x上，可设Q（x0，4x0），则PQ的方程为：

令y＝0，得：

x＝（x0>

1），∴M（，0）

∴S△OQM＝·

·

4x0＝10·

＝10·

[（x0－1）＋＋2]≥40

当且仅当x0－1＝即x0＝2取等号，∴Q（2，8）

PQ的方程为：

，∴x＋y－10＝0

变式训练4.直线l过点M（2，1），且分别交x轴y轴的正半轴于点A、B，O为坐标原点．

（1）当△AOB的面积最小时，求直线l的方程；

（2）当取最小值时，求直线l的方程．

设l：

y－1＝k（x－2）（k＜0）

则A（2－，0），B（0，1－2k）

①由S＝（1－2k）（2－）＝（4－4k－）

≥＝4

当且仅当－4k＝－，即k＝－时等号成立

∴△AOB的面积最小值为4

此时l的方程是x＋2y－4＝0

②∵|MA|·

|MB|＝

＝＝2≥4

当且仅当－k＝－即k＝－1时等号成立

此时l的方程为x＋y－3＝0

（本题也可以先设截距式方程求解）

小结归纳

1．直线方程是表述直线上任意一点M的坐标x与y之间的关系式，由斜率公式可导出直线方程的五种形式．这五种形式各有特点又相互联系，解题时具体选取哪一种形式，要根据直线的特点而定．

2．待定系数法是解析几何中常用的思想方法之一，用此方法求直线方程，要注意所设方程的适用范围．如：

点斜式、斜截式中首先要存在斜率，截距式中横纵截距存在且不为0，两点式的横纵坐标不能相同等（变形后除处）．

3．在解析几何中,设点而不求,往往是简化计算量的一个重要方法.

4．在运用待定数法设出直线的斜率时，就是一种默认斜率存在，若有不存在的情况时，就

会出现解题漏洞，此时就要补救：

较好的方法是看图，数形结合来找差距.

第2课时直线与直线的位置关系

（一）平面内两条直线的位置关系有三种________．

1．当直线不平行坐标轴时，直线与直线的位置关系可根据下表判定

直线

条件

关系

l1：

y＝k1x＋b1

l2：

y＝k2x＋b2

A1x＋B1y＋C1＝0

A2x＋B2y＋C2＝0

平行

重合

相交

（垂直）

2．当直线平行于坐标轴时，可结合图形判定其位置关系．

（二）点到直线的距离、直线与直线的距离

1．P（x0，y0）到直线Ax＋By＋C＝0的距离为______________．

2．直线l1∥l2，且其方程分别为：

Ax＋By＋C1＝0l2：

Ax＋By＋C2＝0，则l1与l2的距离为．

（三）两条直线的交角公式

若直线l1的斜率为k1，l2的斜率为k2，则

1．直线l1到l2的角θ满足．

2．直线l1与l2所成的角（简称夹角）θ满足．

（四）两条直线的交点：

两条直线的交点的个数取决于这两条直线的方程组成的方程组的解的个数．

（五）五种常用的直线系方程.

①过两直线l1和l2交点的直线系方程为A1x＋B1y＋C1＋（A2x＋B2y＋C2）＝0（不含l2）.

②与直线y＝kx＋b平行的直线系方程为y＝kx＋m（m≠b）.

③过定点（x0,y0）的直线系方程为y－y0＝k（x－x0）及x＝x0.

④与Ax＋By＋C＝0平行的直线系方程设为Ax＋By＋m＝0（m≠C）.

⑤与Ax＋By＋C＝0垂直的直线系方程设为Bx－Ay＋C1＝0（AB≠0）.

例2.已知直线l经过两条直线l1：

x＋2y＝0与l2：

3x－4y－10＝0的交点，且与直线l3：

5x－2y＋3＝0的夹角为，求直线l的方程．

由解得l1和l2的交点坐标为（2，－1），因为直线l3的斜率为k3＝，l与l3的夹角为，所以直线l的斜率存在.设所求直线l的方程为y＋1＝k（x－2）．

则tan＝＝

＝1

k＝或k＝－，故所求直线l的方程为y＋1＝－（x－2）或y＋1＝（x－2）即7x＋3y＋11＝0或3x－7y－13＝0

变式训练2.某人在一山坡P处观看对面山顶上的一座铁塔，如图所示，塔高BC=80（米），塔所在的山高OB=220（米），OA=200（米），图中所示的山坡可视为直线l，且点P在直线l上，l与水平地面的夹角为,tan=.试问，此人距水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）？

解如图所示，建立平面直角坐标系，

则A（200，0），B（0，220），C（0，300）.

直线l的方程为y=（x-200）tan,则y=.

设点P的坐标为（x,y），则P（x,）（x＞200）.

由经过两点的直线的斜率公式

kPC=,

kPB=.

由直线PC到直线PB的角的公式得

tan∠BPC=

=

（x＞200）.

要使tan∠BPC达到最大，只需x+-288达到最小，由均值不等式

x+-288≥2-288,

当且仅当x=时上式取得等号.

故当x=320时，tan∠BPC最大.

这时，点P的纵坐标y为y==60.

由此实际问题知0＜∠BPC＜,所以tan∠BPC最大时，∠BPC最大.故当此人距水平地面60米高时，观看铁塔的视角∠BPC最大.

例3.直线y＝2x是△ABC中∠C的平分线所在的直线，若A、B坐标分别为A（－4，2）、B（3，1），求点C的坐标并判断△ABC的形状．

因为直线y＝2x是△ABC中∠C的平分线，所以CA、CB所在直线关于y＝2x对称，而A（－4,2）关于直线y＝2x对称点A1必在CB边所在直线上

设A1（x1，y1）则

得

即A1（4,－2）

由A1（4,－2），B（3,1）求得CB边所在直线的方程为：

3x＋y－10＝0

又由解得C（2,4）

又可求得：

kBC＝－3，kAC＝

∴kBC·

kAC＝－1，即△ABC是直角三角形

变式训练3.三条直线l1：

x+y+a=0，l2：

x+ay+1=0，l3：

ax+y+1=0能构成三角形，求实数a的取值范围。

a∈R且a≠±

1，a≠-2（提示：

因三条直线能构成三角形，故三条直线两两相交且不共点，即任意两条直线都不平行且三线不共点。

（1）若l1、l2、l3相交于同一点，则l1与l2的交点（-a-1，1）在直线l3上，于是a（-a-1）+1+1=0，此时a=1或a=-2。

（2）若l1∥l2，则-1=-

，a=1。

（3）若l1∥l3，则-1=-a，a=1。

（4）若l2∥l3，则-

=-a，a=±

1。

）

例4.设点A（－3，5）和B（2，15），在直线l：

3x－4y＋4＝0上找一点p，使为最小，并求出这个最小值．

设点A关于直线l的对称点A'

的坐标为（a，b），则由AA´

⊥l和AA´

被l平分，

则

解之得a＝3，b＝－3，∴A´

＝（3，－3）．∴（|PA|＋|PB|）min＝|A´

B|＝5

∵kA´

B＝＝－18

∴A´

B的方程为y＋3＝－18（x－3）

解方程组得P（，3）

变式训练4：

已知过点A（1，1）且斜率为－m（m>

0）的直线l与x、y轴分别交于P、Q两点，过P、Q作直线2x＋y＝0的垂线，垂足分别为R、S，求四边形PRSQ的面积的最小值．

设l的方程为y－1＝－m（x－1），

则P（1＋，0），Q（0，1＋m）

从则直线PR：

x－2y－＝0；

直线QS：

x－2y＋2（m＋1）＝0又PR∥QS

∴|RS|＝＝

又|PR|＝，|QS|＝

而四边形PRSQ为直角梯形，

∴SPRSQ＝×

（）×

＝（m＋＋）2－≥（2＋）2－

＝3.6

∴四边形PRSQ的面积的最小值为3.6．

1．处理两直线位置关系的有关问题时，要注意其满足的条件．如两直线垂直时，有两直线斜率都存在和斜率为O与斜率不存在的两种直线垂直．

2．注意数形结合，依据条件画出图形，充分利用平面图形的性质和图形的直观性，有助于问题的解决．

3．利用直线系方程可少走弯路，使一些问题得到简捷的解法．

4．解决对称问题中，若是成中心点对称的，关键是运用中点公式，而对于轴对称问题，一般是转化为求对称点，其关键抓住两点：

一是对称点的连线与对称轴垂直；

二是两对称点的中点在对称轴上，如例4

第3课时线性规划

1．二元一次不等式表示的平面区域．

⑴一般地，二元一次不等式Ax＋By＋C>

0在平面直角坐标系中表示直线Ax＋By＋C＝0某一侧的所有点组成的平面区域（半平面）不含边界线，不等式Ax＋By＋C≥0所表示的平面区域（半平面）包括边界线．

⑵对于直线Ax＋By＋C＝0同一侧的所有点（x、y）使得Ax＋By＋C的值符号相同．因此，如果直线Ax＋By＋C＝0一侧的点使Ax＋By＋C>

0，另一侧的点就使Ax＋By＋C<

0，所以判定不等式Ax＋By＋C>

0（或Ax＋By＋C<

0）所表示的平面区域时，只要在直线Ax＋By＋C＝0的一侧任意取一点（x0，y0），将它的坐标代入不等式，如果该点的坐标满足不等式，不等式就表示该点所在一侧的平面区域；

如果不满足不等式，就表示这个点所在区域的另一侧平面区域．

⑶由几个不等式组成的不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分．

2．线性规划

⑴基本概念

名称

意义

线性约束条件

由x、y的一次不等式（或方程）组成的不等式组,是对x、y的约束条件

目标函数

关于x、y的解析式如：

z＝2x＋y，z＝x2＋y2等

线性目标函数

关于x、y的一次解析式

可行解

满足线性约束条件x、y的解（x，y）叫做可行解

可行域

所有可行解组成的集合叫做可行域

最优解

使目标函数达到最大值或最小值的可行解

线性规划问题

求线性目标函数在线性约束条件下的最大值或最小值的问题

⑵用图解法解决线性规划问题的一般步骤：

①设出所求的未知数；

②列出约束条件（即不等式组）；

③建立目标函数；

④作出可行域和目标函数的等值线；

⑤运用图解法即平行移动目标函数等值线，求出最优解．（有些实际问题应注意其整解性）

例1.若△ABC的三个顶点为A（3，－1），B（－1，1），C（1，3），写出△ABC区域（含边界）表示的二元一次不等式组．

由两点式得AB、BC、CA直线的方程并化简得AB：

x＋2y－1＝0，BC：

x－y＋2＝0，CA：

2x＋y－5＝0

结合区域图易得不等式组为

变式训练1：

△ABC的三个顶点为A（2，4）、B（－1，2）、C（1，0），则△ABC的内部（含边界）可用二元一次不等式组表示为．

例2.已知x、y满足约束条件分别求：

⑴z＝2x＋y

⑵z＝4x－3y

⑶z＝x2+y2的最大值、最小值？

在直角坐标系中作出表示不等式组的公共区域如图阴影部分．

其中A（4，1），

B（－1，－6），

C（－3，2）

（1）作与直线2x＋y＝0平行的直线l1：

2x＋y＝t，则当l1经过点A时，t取最大，l1经过点B时，t取最小．

∴zmax＝9zmin＝－13

（2）作与直线4x－3y＝0平行的直线l2：

4x－3y＝t，则当l2过点C时，t最小，l2过点B时，t最大．

∴zmax＝14zmin＝－18

（3）由z＝x2＋y2，则表示点（x，y）到（0，0）的距离，结合不等式组表示的区域．知点B到原点的距离最大，当（x，y）为原点时距离为0．∴zmax＝37zmin＝0

变式训练2：

给出平面区域如下图所示，目标函数t＝ax－y，

（1）若在区域上有无穷多个点（x，y）可使目标函数t取得最小值，求此时a的值．

（2）若当且仅当x＝，y＝时，目标函数t取得最小值，求实数a的取值范围？

（1）由t＝ax－y得y＝ax－t

要使t取得最小时的（x，y）有无穷多个，

则y＝ax－t与AC重合．

∴a＝kAC＝

＝－

（2）由KAC<

a<

KBC得－<

－.

例3.某木器厂生产圆桌子和衣柜两种产品，现有两种木料，第一种72立方米，第二种有56立方米，假设生产每种产品都需要用两种木料，生产一张圆桌需用第一种木料0.18立方米，第二种木料0.08立方米，可获利润6元，生产一个衣柜需用第一种木料0.09立方米，第二种0.28立方米，可获利10元，木器厂在现有木料条件下，圆桌和衣柜应各生产多少才能使所获利润最多？

设圆桌和衣柜的生产件数分别为x、y，所获利润为z，则：

即

则z＝6x＋10y作出可行域如图．

由

得

即M（350，100）

由图可知，当直线l：

6x＋10y＝0平移到经过点M（350，100）时，z＝6x＋10y最大，即当x＝350，y＝100时，，z＝6x＋10y最大．

变式训练3：

某厂要生产甲种产品45个，乙种产品55个，可用原料为A、B两种规格的金属板，每张面积分别为2m2和3m2，用A种可造甲种产品3个和乙种产品5个，用B种可造甲、乙两种产品各6个．问A、B两种产品各取多少块可保证完成任务，且使总的用料（面积）最小．

设A种取x块，B种取y块，总用料为zm2，则

z＝2x＋3y（x、y∈N）

可行域如图：

最优解为A（5，5），x＝5，y＝5时，zmin＝25，即A、B两种各取5块时可保证完成任务，且总的用料（面积）最省为25m2．

例4.预算用xx元购买单价为50元桌子和20元的椅子，希望桌子的总数尽可能的多，但解：

椅子的总数不能少于桌子的总数，但不多于桌子数的1.5倍，问桌椅各买多少才合适？

设桌椅分别买x、y张，由题意得：

由

解得：

∴点A（，）

由解得

∴点B（25，）

满足以上不等式组表示的区域是以A、B、O为顶点的△AOB及内部设x＋y＝z，即y＝－x＋z；

当直线过点B时，即x＝25，y＝，z最大．∵y∈z，∴y＝37

∴买桌子25张，椅子37张是最优选择．

A1、A2两煤矿分别有煤8万吨和18万吨，需通过外运能力分别为20万吨和16万吨的B1、B2两车站外运，用汽车将煤运到车站，A1的煤运到B1、B2的运费分别为3元/吨和5元/吨，A2的煤运到B1、B2的运费分别为7元/吨和8元/吨，问如何设计调运方案可使总运费最少？

设A1运到B1x万吨，A2运到B1y万吨，总运费为z万元，则A1运到B2（8－x）万吨，A2运到B2（18－y）万吨，z＝3x＋5（8－x）＋7y＋8（18－y）＝184－2x－y，x、y满足

可行域如图阴影部分．

当x＝8时，y＝12时，zmin＝156

即A1的8万吨煤全运到B1，A2运到12万吨运到B1，剩余6万吨运到B2，这时总运费最少为156万元．

1．二元一次不等式或不等式组表示的平面区域：

①直线确定边界；

②特殊点确定区域．

2．线性规划实际上是“数形结合”的数学思想的体现，是一种求最值的方法．

3．把实际问题抽象转化为数学问题是本节的重难点，求解关键是根据实际问题中的已知条件，找出约束条件和目标函数，利用图解法求得最优解．而在考虑约束条件时，除数学概念的条件约束外，还要深入其境、考虑实际意义的约束．

4．解线性规划问题的关键步骤是在图上完成的，所以作图尽可能精确，图上操作尽可能规范。

但最优点不易辨别时，要逐一检查.

第4课时曲线与方程

、

1．直接法求轨迹的一般步骤：

建系设标，列式表标，化简作答（除杂）．

2．求曲线轨迹方程，常用的方法有：

直接法、定义法、代入法（相关点法、转移法）、参数法、交轨法等．

例1.如图所示，过点P（2，4）作互相垂直的直线l1、l2.若l1交x轴于A，l2交y轴于B，求线段AB中点M的轨迹方程.

解：

设点M的坐标为（x,y）,

∵M是线段AB的中点，

∴A点的坐标为（2x,0），B点的坐标为（0，2y）.

∴=（2x-2，-4），=（-2，2y-4）.

由已知·

=0，∴-2（2x-2）-4（2y-4）=0，

即x+2y-5=0.

∴线段AB中点M的轨迹方程为x+2y-5=0.

已知两点M（-2，0）、N（2，0），点P为坐标平面内的动点，满足||||+·

=0，求动点P（x，y）的轨迹方程.

解由题意：

=（4，0），=（x+2,y）,

=（x-2,y）,

∵||||+·

=0，

∴·

+（x-2）·

4+y·

0=0，

两边平方，化简得y2=-8x.

例2.在△ABC中，A为动点，B、C为定点，B,C且满足条件sinC-sinB=sinA,则动点A的轨迹方程是（）

A.=1（y≠0）B.=1（x≠0）

C.=1（y≠0）的左支D.=1（y≠0）的右支

已知圆C1：

（x+3）2+y2=1和圆C2：

（x-3）2+y2=9,动圆M同时与圆C1及圆C2相外切，求动圆圆心M的轨迹方程.

解如图所示，设动圆M与圆C1及圆C2分别外切于点A和点B，根据两圆外切的充要条件，得

|MC1|-|AC1|=|MA|，

|MC2|-|BC2|=|MB|.

因为|MA|=|MB|，

所以|MC2|-|MC1|=|BC2|-|AC1|=3-1=2.

这表明动点M到两定点C2，C1的距离之差是常数2.

根据双曲线的定义，动点M的轨迹为双曲线的左支（点M到C2的距离大，到C1的距离小），这里a=1,c=3,则b2=8,设点M的坐标为（x,y）,其轨迹方程为x2-=1（x≤-1）.

例3.如图所示，已知P（4，0）是圆x2+y2=36内的一点，A、B是圆上两动点，

且满足∠APB=90°

，求矩形APBQ的顶点Q的轨迹方程.

解设AB的中点为R，坐标为（x1，y1），Q点坐标为（x，y），

则在Rt△ABP中，

|AR|=|PR|，

又因为R是弦AB的中点，依垂径定理有

Rt△OAR中，|AR|2=|AO|2-|OR|2=36-（）.

又|AR|=|PR|=，

所以有（x1-4）2+=36-（）.

即-4x1-10=0.

因为R为PQ的中点，

所以x1=，y1=.

代入方程-4x1-10=0，得

-10=0.

整理得x2+y2=56.

这就是Q点的轨迹方程.

设F（1，0），M点在x轴上，P点在y轴上，且=2，⊥，当点P

在y轴上运动时，求点N的轨迹方程.

解设M（x0，0），P（0，y0），N（x，y），

由=2得（x-x0，y）=2（-x0，y0），

∴即

∵⊥,=（x0,-y0）,=（1,-y0）,

∴（x0,-y0）·

（1，-y0）=0,∴x0+=0.