特殊平行四边形知识点总结及题型Word格式.docx
《特殊平行四边形知识点总结及题型Word格式.docx》由会员分享,可在线阅读,更多相关《特殊平行四边形知识点总结及题型Word格式.docx(13页珍藏版)》请在冰豆网上搜索。
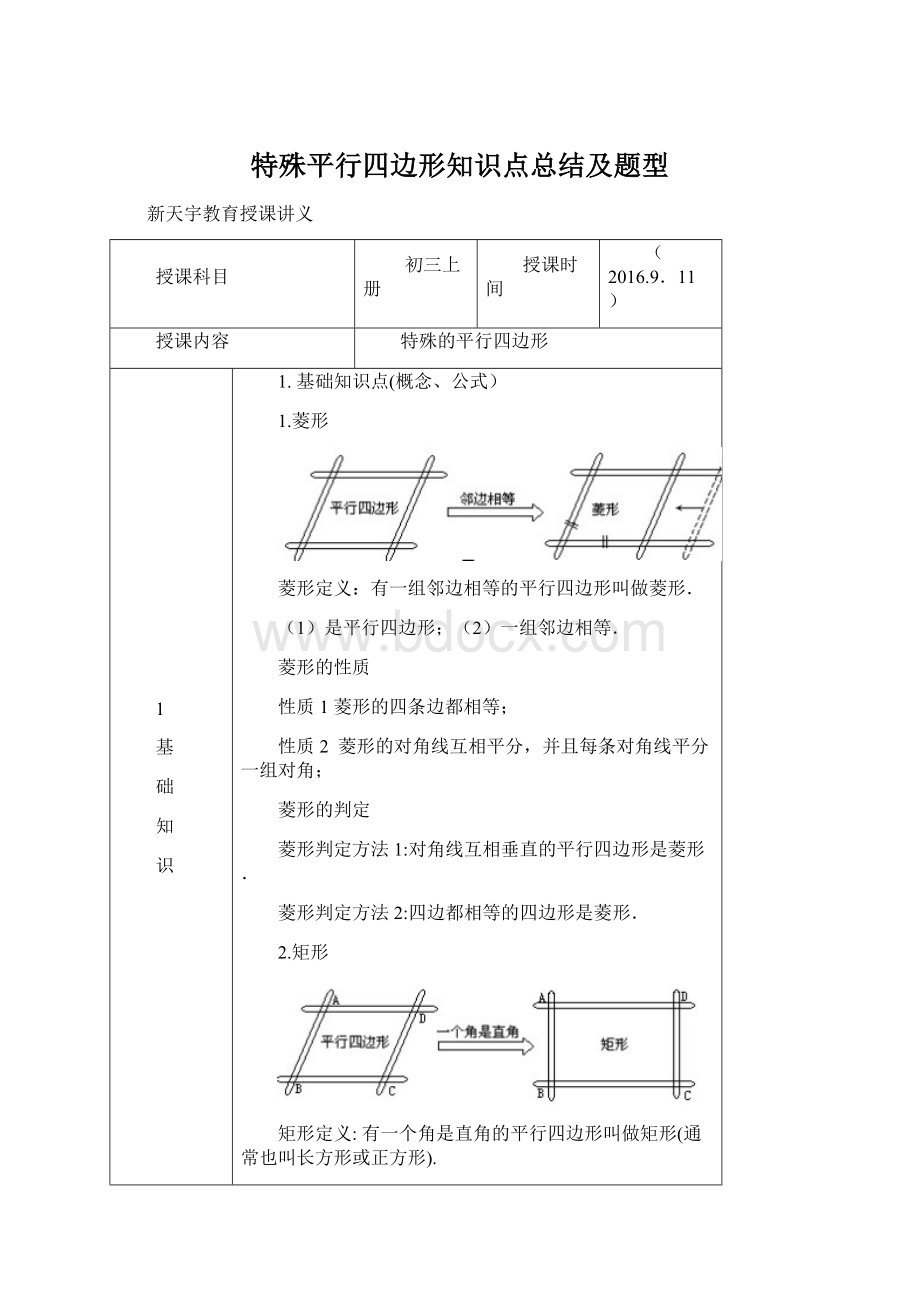
菱形的判定
菱形判定方法1:
对角线互相垂直的平行四边形是菱形.
菱形判定方法2:
四边都相等的四边形是菱形.
2.矩形
矩形定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形或正方形).
矩形是中心对称图形,对称中心是对角线的交点,矩形也是轴对称图形,对称轴是通过对边中点的直线,有两条对称轴;
矩形的性质:
(具有平行四边形的一切特征)
矩形性质1:
矩形的四个角都是直角.
矩形性质2:
矩形的对角线相等且互相平分.
矩形的判定方法.
矩形判定方法1:
对角钱相等的平行四边形是矩形.
矩形判定方法2:
有三个角是直角的四边形是矩形.
矩形判定方法3:
有一个角是直角的平行四边形是矩形.
矩形判定方法4:
对角线相等且互相平分的四边形是矩形.
2.正方形
正方形是在平行四边形的前提下定义的,它包含两层意思:
①有一组邻边相等的平行四边形(菱形
②有一个角是直角的平行四边形(矩形)
正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形.
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.正方形是中心对称图形,对称中心是对角线的交点,正方形又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,共有四条对称轴;
因为正方形是平行四边形、矩形,又是菱形,所以它的性质是它们性质的综合,正方形的性质总结如下:
边:
对边平行,四边相等;
角:
四个角都是直角;
对角线:
对角线相等,互相垂直平分,每条对角线平分一组对角.
注意:
正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°
;
正方形的两条对角线把它分成四个全等的等腰直角三角形,这是正方形的特殊性质.
正方形具有矩形的性质,同时又具有菱形的性质.
正方形的判定方法:
(1)有一个角是直角的菱形是正方形;
(2)有一组邻边相等的矩形是正方形.
1、正方形概念的三个要点:
(2)有一个角是直角;
(3)有一组邻边相等.
2、要确定一个四边形是正方形,应先确定它是菱形或是矩形,然后再加上相应的条件,确定是正方形.
2.本节课的重点、难点
(1)对平行四边形和特殊的几种图形的性质要注意理解
(2)对证明特殊平行四边形的方法进行掌握
3.学生容易混淆的知识点
(1)各种四边形对角线的特点。
(2)各种特殊平行四边形的证明方式。
4.针对不同层次学生的题型
例1.矩形
1已知:
如图,矩形ABCD,AB长8cm,对角线比AD边长4cm.求AD的长及点A到BD的距离AE的长.
2已知:
如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC.求证:
CE=EF.
3.如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.
4、如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:
AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC
是矩形,并说明理由.
例2.菱形
1
已知:
如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:
∠AFD=∠CBE.
2已知:
如图
ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.求证:
四边形AFCE是菱形.
3、如图,在ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F,求证:
四边形AFCE是菱形.
4、已知如图,菱形ABCD中,E是BC上一点,AE、BD交于M,
若AB=AE,∠EAD=2∠BAE。
求证:
AM=BE。
5.(10湖南益阳)如图,在菱形ABCD中,∠A=60°
=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1)求线段
的长.
6、如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC,交BC的延长线于F。
请你猜想DE与DF的大小有什么关系?
并证明你的猜想
例3.正方形
1已知:
如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
OE=OF.
2
精
讲
例
题
2已知:
如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
四边形PQMN是正方形
3.如图所示,在正方形ABCD中,M为AB的中点,
,BN平分
并交MN于N。
MD=MN。
4
课
后
作
业
作业:
1.以不在同一直线上的三个点为顶点作平行四边形,最多能作(
)
A.4个
B.3个
C.2个
D.1个
2.若平行四边形的一边长为10cm,则它的两条对角线的长度可以是(
);
A.5cm和7cm
B.18cm和28cm
C.6cm和8cm
D.8cm和12cm
3.如图,平行四边形ABCD中,经过两对角线交点O的直线分别交BC于点E,交AD于点F.若BC=7,CD=5,OE=2,则四边形ABEF的周长等于(
).
A.14
B.15
C.16
D.无法确定
4.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )
A.4
B.6
C.8
D.10
5.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°
的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°
或30°
B.30°
或45°
C.45°
或60°
D.30°
6.如图,菱形ABCD中,对角线AC、BD交于点O,菱形ABCD周长为32,点P是边CD的中点,则线段OP的长为(
A.3
B.5
C.8
D.4
7.如图,在平行四边形ABCD中,过对角线BD上一点P,作EF∥BC,HG∥AB,若四边形AEPH和四边形CFPG的面积分另为S1和S2,则S1与S2的大小关系为( )
A.S1=S2
B.S1>S2
C.S1<S2
D.不能确定
8.矩形的两条对角线所成的钝角为120°
,若一条对角线的长是2,那么它的周长是(
A.6
B.
C.2(1+
D.1+
9.如图,菱形ABCD中,∠A=120°
,E是AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F,那么∠BFC的度数是( )
A.60°
B.70°
C.75°
D.80°
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点.若AC=8,BD=6,则四边形EFGH的面积为(
A.14
B.12
C.24
D.48
11.如图,在菱形ABCD中,AC,BD是对角线,如果∠BAC=70°
,
那么∠ADC等于
.
12.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,若AC=4,则四边形CODE的周长为
13.如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;
点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 2或
秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
14.如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.则折痕EF的最大值是 cm.
15.如图,将两条宽度都是为2的纸条重叠在一起,使∠ABC=45°
,则四边形ABCD的面积为 _________ .
16.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为
17.如图,菱形ABCD的边长为4,∠BAD=120°
,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是
.
18.如图,菱形ABCD中,AB=2,∠BAD=60°
,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是
19.如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:
四边形EFGH是菱形.
20.如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:
四边形ABCD是菱形.
21.如图,在菱形ABCD中,∠ABC=60°
,过点A作AE⊥CD于点E,交对角线BD于点F,过点F作FG⊥AD于点G.
BF=AE+FG;
(2)若AB=2,求四边形ABFG的面积.
22.如图,△ABC中,AD是边BC上的中线,过点A作AE//BC,过点D作DE//AB,DE与AC、AE分别交于点O、点E,连接EC.
AD=EC;
(2)当∠BAC=Rt∠时,求证:
四边形ADCE是菱形.
23.将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.
△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?
证明你的结论.
24.已知:
矩形ABCD中,对角线AC与BD交与点O,∠BOC=120°
,AC=4cm.求:
矩形ABCD的周长和面积。