反比例函数的综合题.docx

反比例函数的综合题.docx

《反比例函数的综合题.docx》由会员分享，可在线阅读，更多相关《反比例函数的综合题.docx（10页珍藏版）》请在冰豆网上搜索。

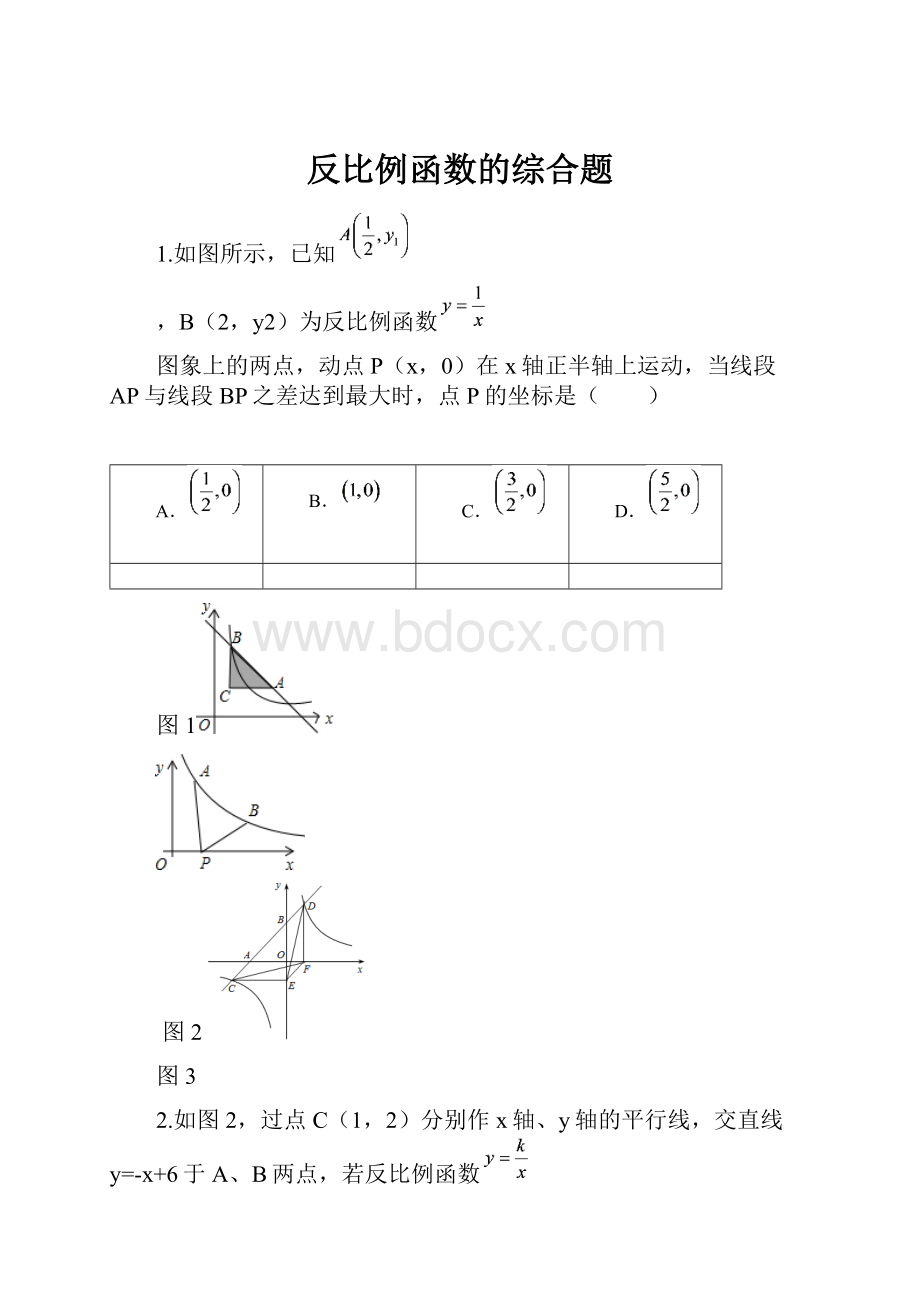
反比例函数的综合题

1.如图所示，已知

，B（2，y2）为反比例函数

图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（　　）

A．

B．

C．

D．

图1

图2

图3

2.如图2，过点C（1，2）分别作x轴、y轴的平行线，交直线y=-x+6于A、B两点，若反比例函数

（x＞0）的图象与△ABC有公共点，则k的取值范围是（　　）

A．2≤k≤9

B．2≤k≤8

C．2≤k≤5

D．5≤k≤8

3.如图3，一次函数y=x+3的图象与x轴，y轴交于A，B两点，与反比例函数

的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：

①△CEF与△DEF的面积相等；②△AOB∽△FOE；③△DCE≌△CDF；④AC=BD．

其中正确的结论是（　　）

A．①②

B．①②③

C．①②③④

D．②③④

4，如图，双曲线

经过点A（2，2）与点B（4，m），则△AOB的面积为（　　）

A．2

B．3

C．4

D．5

5．如图，点P是双曲线

（k1＜0，x＜0）上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交双曲线

（0＜k2＜|k1|）于E、F两点．

（1）图1中，四边形PEOF的面积S1。

（用含k1、k2的式子表示）

（2）图2中，设P点坐标为（-4，3）．

①判断EF与AB的位置关系，并证明你的结论；

②记S2=S△PEF-S△OEF，S2是否有最小值？

若有，求出其最小值；若没有，请说明理由．

6．（2009•绥化）直线

与坐标轴分别交于A、B两点，动点P、Q同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O⇒B⇒A运动．

（1）直接写出A、B两点的坐标；

（2）设点Q的运动时间为t（秒），△OPQ的面积为S，求出S与t之间的函数关系式；

（3）当

时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标．

7．（2007•益阳）如图1，M是边长为4的正方形AD边的中点，动点P自A点起，由A⇒B⇒C⇒D匀速运动，直线MP扫过正方形所形成的面积为Y，点P运动的路程为X，请解答下列问题：

（1）当x=1时，求y的值；

（2）就下列各种情况，求y与x之间的函数关系式：

①0≤x≤4；②4＜x≤8③8＜x≤12；

（3）在给出的直角坐标系（图2）中，画出

（2）中函数的图象．

8．（2009•邵阳）如图，直线l的解析式为y=-x+4，它与x轴、y轴分别相交于A、B两点，平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴、y轴分别相交于M、N两点，运动时间为t秒（0＜t≤4）

（1）求A、B两点的坐标；

（2）用含t的代数式表示△MON的面积S1；

（3）以MN为对角线作矩形OMPN，记△MPN和△OAB重合部分的面积为S2；

①当2＜t≤4时，试探究S2与之间的函数关系；

②在直线m的运动过程中，当t为何值时，S2为△OAB的面积的

？

9．（2007•台州）如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边BC折叠，使点B落在边OA的点D处．已知折叠

．

（1）判断△OCD与△ADE是否相似？

请说明理由；

（2）求直线CE与x轴交点P的坐标；

（3）是否存在过点D的直线l，使直线l、直线CE与x轴所围成的三角形和直线l、直线CE与y轴所围成的三角形相似？

如果存在，请直接写出其解析式并画出相应的直线；如果不存在，请说明理由．

10．如图，在平面直角坐标系中，四边形OABC为直角梯形，OA∥BC，BC=14，A（16，0），C（0，2）．

（1）如图①，若点P、Q分别从点C、A同时出发，点P以每秒2个单位的速度由C向B运动，点Q以每秒4个单位的速度由A向O运动，当点Q停止运动时，点P也停止运动．设运动时间为t秒（0≤t≤4）．

①求当t为多少时，四边形PQAB为平行四边形？

②求当t为多少时，直线PQ将梯形OABC分成左右两部分的比为1：

2，并求出此时直线PQ的解析式．

（2）如图②，若点P、Q分别是线段BC、AO上的任意两点（不与线段BC、AO的端点重合），且四边形OQPC面积为10，试说明直线PQ一定经过一定点，并求出该定点的坐标．

11．（2010•密云县）附加题：

已知：

如图，正比例函数y=ax的图象与反比例函数

的图象交于点A（3，2）

（1）试确定上述正比例函数和反比例函数的表达式；

（2）根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值；（3）M（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点M作直线MN∥x轴，交y轴于点B；过点A作直线AC∥y轴交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．

12．（2008•湖州）已知：

在矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是边BC上的一个动点（不与B，C重合），过F点的反比例函数

（k＞0）的图象与AC边交于点E．

（1）求证：

△AOE与△BOF的面积相等；

（2）记S=S△OEF-S△ECF，求当k为何值时，S有最大值，最大值为多少？

（3）请探索：

是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？

若存在，求出点F的坐标；若不存在，请说明理由．

13．（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（-2，-1），且P（-1，-2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．

（1）写出正比例函数和反比例函数的关系式；

（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？

如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．

14．（2006•大连）如图，直线y=k和双曲线

相交于点P，过P点作PA0垂直x轴，垂足为A0，x轴上的点A0、A1、A2、…An的横坐标是连续的整数，过点A1、A2、…An分别作x轴的垂线，与双曲线

（x＞0）及直线y=k分别交于点B1、B2、…Bn，C1、C2、…Cn．

（1）求A0点坐标；

（2）求

及

的值；（3）试猜想

的值。

15．已知一次函数y=kx+b与双曲线

在第一象限交于A、B两点，A点横坐标为1．B点横坐标为4．

（1）求一次函数的解析式；

（2）根据图象指出不等式

的解集；

（3）点P是x轴正半轴上一个动点，过P点作x轴的垂线分别交直线和双曲线于M、N，设P点的横坐标是t（t＞0），△OMN的面积为S，求S和t的函数关系式，并指出t的取值范围．

16．（2008•莱芜）

（1）探究新知：

如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．

（2）结论应用：

①如图2，点M，N在反比例函数

（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F，试证明：

MN∥EF；

②若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断MN与EF是否平行．