练习1文档格式.docx

练习1文档格式.docx

《练习1文档格式.docx》由会员分享，可在线阅读，更多相关《练习1文档格式.docx（12页珍藏版）》请在冰豆网上搜索。

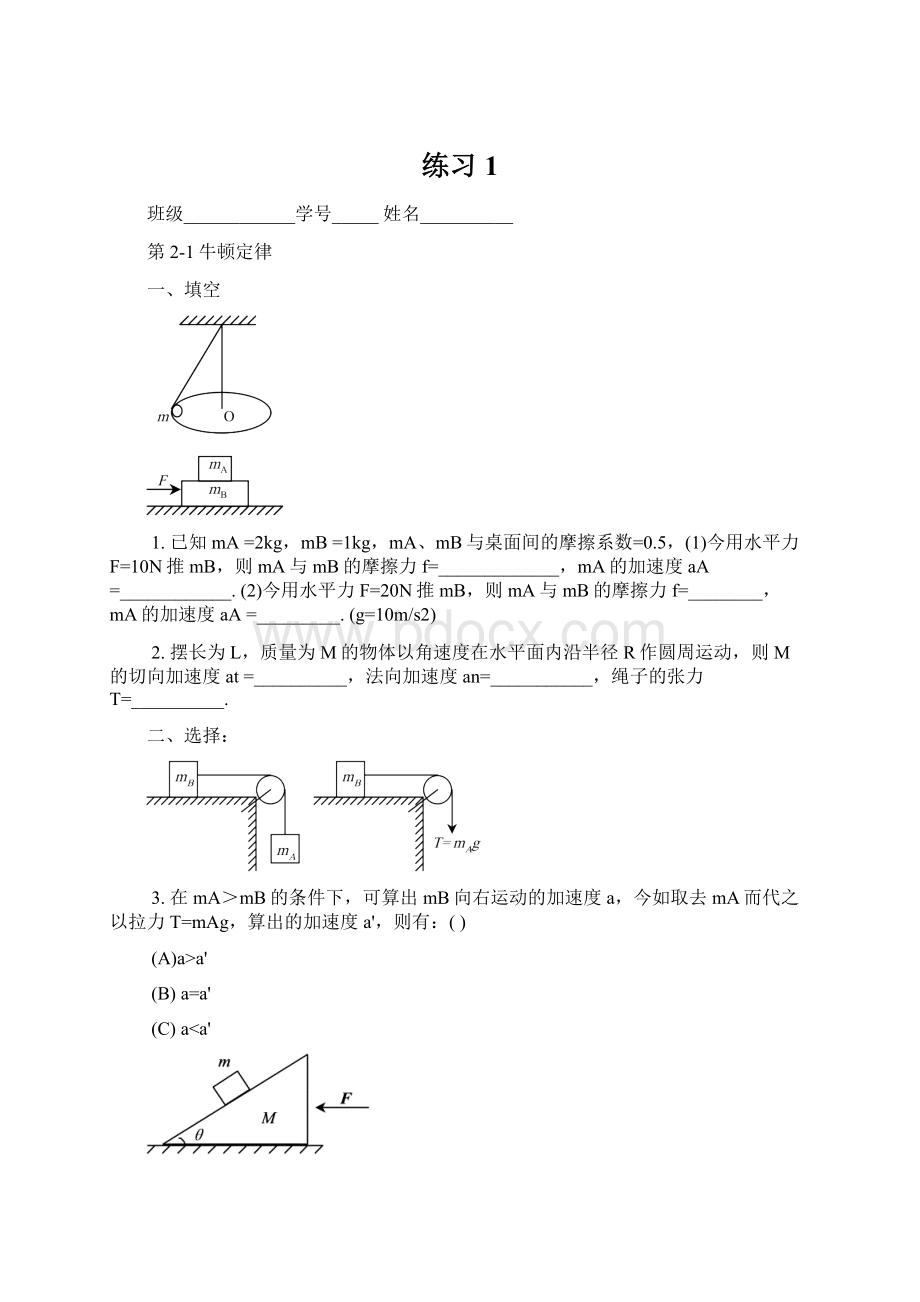
（B）a=a'

（C）a<

4.m与M水平桌面间都是光滑接触，为维持m与M相对静止，则推动M的水平力F为：

（A）（m+M）gctg（B）（m+M）gtg

（C）mgtg（D）Mgtg

三、计算题与证明：

5.把一个质量m的木块放在与水平成角的固定斜面上，两者间的静摩擦系数s较小，因此如不加支持，木块将加速下滑，

（1）证明：

tg>

s.

（2）须加多大的水平力F，可使木块恰不下滑？

此时木块对斜面的正压力？

*（3）如不断增大F力的量值，则摩擦力和正压力将怎样变化？

6.重物A和B的质量分别为mA和mB，用一细线连接挂在定滑轮两边，此二物体可沿三棱柱面滑动如图所示，设物体与三棱柱面间的摩擦系数为，角、均为已知，重物初速度为零，绳和滑轮质量可略去不计，试证重物的平衡条件为：

7.一细绳穿过一光滑细管，两端分别拴着质量为m和M的小球，管子保持竖直位置不动，当小球m绕管子的几何轴转动时，系它的绳子与竖直方向夹角为，如图中所示，设小球m到管口的绳子长为L，且L>

>

细管半径.

（1）证明：

cos=m/M；

小球m所受向心力Fn=Mg

（2）证明：

小球转动的周期T=2

班级＿＿＿＿＿学号＿＿＿姓名＿＿＿＿＿

第２－２习题课（牛顿运动定律）

1.一细绳跨过一定滑轮，绳的一边悬有一质量为m1的物体，另一边穿在质量为m2的圆柱体的竖直细孔中，圆柱体可沿绳滑动，今看到绳子从圆柱细孔中加速上升，圆柱体相对于绳子以匀加速度a'

下滑，求m1、m2相对地面的加速度、绳子的张力以及柱体与绳子的摩擦力.（绳的质量，滑轮的质量以及滑轮转动摩擦都不计）

2.在倾角为30°

的固定光滑斜面上放一质量为M的楔形滑块，其上表面与水平面平行，在其上放一质量为m的小球（如图），M与m间无摩擦，且M=2m，试求小球的加速度及楔形滑块对斜面的作用力.

3.光滑水平面上平放着半径的R的固定环，环内的一物体以速率v0开始沿环内侧逆时针方向运动，物体与环内侧的摩擦系数为，求：

（1）物体任一时刻t的速率v，

（2）物体从开始运动经t秒经历的路程S.

4.质量为M的机动小船在快靠岸时关闭发动机，此时的船速为v0，设水对小船的阻力R正比于船速v，即R=kv（k为比例系数），求小船在关闭发动机后还能前进多远？

*5.一小环A套在半径为a的竖直大圆环上，小环与大环之间的摩擦系数为，证明：

当大环以匀角速绕它自己水平轴O转动时，如果

则小环与大环之间无相对运动.（提示：

先求出大环对小环的法向支承力N，要求其大小不能为虚数）

班级____________学号____________姓名_________

第2-3运动学牛顿定律（习题课后作业）

一、填空：

1.质量为m的质点沿X轴正向运动，设质点通过坐标点为x时的速度为kx（k为常数），则作用在质点的合外力F=_________.质点从x=x0到x=2x0处所需的时间t=________.

二.选择题：

2.体重身高相同的甲乙两人，分别用双手握住跨过无摩擦轻滑轮的绳子各一端，他们由初速为零向上爬，经过一定时间，甲相对绳子的速率是乙相对绳子速率的两倍，则到达顶点的情况是：

（A）甲先到达（B）乙先到达（C）同时到达（D）不能确定

3.一质量为m的质点，自半径为R的光滑半球形碗口由静止下滑，质点在碗内某处的速率为v，则质点对该处的压力数值为：

（A）

（B）

（C）

（D）

4.如图所示，用一斜向上的力F（与水平成30°

角），将一重为G的木块压靠竖直壁面上，如果不论用怎样大的力F，都不能使木块向上运动，则说明木块与壁面间的静摩擦系数的大小为：

（A）≥1/2（B）≥1/

（C）≥2

（D）≥

三、计算题：

5.桌上有一块质量M=1kg的木板，板上放着一个质量m=2kg的物体，物体与板之间，板和桌面之间的滑动摩擦系数均为k=0.25，静摩擦系数均为s=0.30.

（1）现以水平力F拉板，物体与板一起以加速度v=1ms-2运动，求：

物体和板的相互作用力以及板和桌面的相互作用力，

（2）现在要使板从物体下抽出，须用的力F要加到多大？

6.一个重量为P的质点，在光滑的固定斜面上以初速v0运动，v0方向与斜面底边水平线AB平行（如图所示），求这质点的运动轨道（斜面倾向为）

7.一个质量m=4kg的物体，用两根长度各为l=1.25m的细绳系在竖直杆上相距b=2m的两点，当此系统绕杆的轴转动时，绳子被拉开，情况如图所示.

（1）要使上方绳子有T1=60N的张力，此系统的转速要多大？

（2）这时下方绳子的张力T2又有多大？

班级____________学号_____姓名________

第2-4动量定理

1.物体所受冲力F与时间的图线如图所示，则该曲线与横坐标t所围成的面积表示物体在t=t2-t1时间所受的__________.

2.如图，作匀速圆周运动的物体，从A运动到B的过程中，物体所受合外力的冲量：

（A）大小为零

（B）大小不等于零，方向与vA相同

（C）大小不等于零，方向与vB相同

（D）大小不等于零，方向与物体在B点所受合力相同

3.设有三个质量完全相同的物体，在某时刻t它们的速度分别为v1、v2、v3，并且v1=v2=v3，v1与v2方向相反，v3与v1相垂直，设它们的质量全为m，试问该时刻三物体组成的系统的总动量为_______________.

4.质量为m的物体以初速度v0，倾角斜向抛出，不计空气阻力，抛出点与落地点在同一水平面，则整个过程中，物体所受重力的冲量大小为______________，方向为_______________.

5.用棒打击一质量0.30kg，速率为20ms-1的水平飞来的球，球飞到竖直上方10m的高度，求棒给予球的冲量为多少？

设球与棒的接触时间为0.02s，求球受到的平均冲力.

6.一个步兵，他和枪的质量共为100kg，穿着带轮的溜冰鞋站着，现在他用自动枪在水平方向射出10发子弹，每颗子弹的质量为10g，而出口的速度为750ms-1，如果步兵无摩擦地向右运动，问在第十次发射后他的速度是多少？

7.三个物体A、B、C每个的质量均为M，B、C靠在一起，放在光滑水平桌面上，两者间连有一段长度为0.4m的细绳，原先放松着，B的另一端则连有另一细绳，跨过桌边的定滑轮而与A相连（见图），已知滑轮和绳子的质量不计，滑轮轴上的摩擦也可忽略，绳子长度一定，问A、B起动后经多长时间C也开始运动？

B、C具有相同速度时，其速度大小为多少？

（取g=10ms-2）

班级＿＿＿＿＿学号＿＿＿姓名＿＿＿＿

第2-5动能定理

　１.如图，有人用恒力F，通过轻绳和轻滑轮，将一木块从位置A拉到位置B，设物体原来位置AC=L0，后来位置BC=L，物体水平位移为S，则在此过程中，人所作的功为__________.

　２.一链条垂直悬挂于A点，质量为m，长为L，今将其自由端B也挂在A点，则外力需做的功为_____________.

　３.系统总动量守恒的条件是：

__________________________________________.系统总机械能守恒的条件是：

_____________________________________________.

　４.已知地球质量为M，半径为R，一质量为m的火箭从地面上升到距地面高度为2R处，在此过程中，地球引力对火箭作的功为_____________.

　５.一个质点在几个力同时作用下的位移为r=（4i-5j+6k）米，其中一个恒力可表达成Ｆ=（-3i-5j+9k）牛顿，这个力在这过程中做功为____________.

　６.一个质量为ｍ=2kg的质点，在外力作用下，运动方程为：

x=5+t2，y=5t-t2，则力在t=0到t=2秒内作的功为______________.

　７.如图，一轻弹簧原长为L0与圆环半径R相等，当弹簧下端悬质量为m的小球时，弹簧总长Ｌ=2R，小球刚好达到平衡，现将弹簧一端固定于竖直放置的圆环上端A点，将挂小球的另一端套在光滑圆环的B点，AB长为1.6R，放手后小球从静止开始沿圆环滑动，求：

（1）球从Ｂ沿圆环滑到最低点Ｃ处的过程中，小球、弹簧和地球组成的系统势能的增量，

（2）小球滑到Ｃ点时对圆环的压力.

８.一质量为ｍ的物体，从质量为Ｍ的圆弧形槽顶端由静止滑下，设圆弧形槽的半径为Ｒ，张角为/2，如图所示，如所有摩擦都可忽略，求：

（1）物体刚离开槽底时，物体和槽的速度各是多少？

（2）在物体从Ａ滑到Ｂ的过程中，物体对槽做的功为多少？

（3）物体到达Ｂ点时，对槽的压力（Ｂ点为槽的最底端）.

９.用一弹簧把质量各为m1和m2的两木块连起来，一起放在地面上，弹簧的质量可不计，而m2>

m1，问

（1）对上面的木块必须施加多大的压力Ｆ，以便在Ｆ突然撒去而上面的木块跳起来时，恰能使下面的木块提离地面？

（2）如m1和m2互换位置，结果有无改变？

第2-6　守恒定律（习题课）

　１.两质量分别为m1、m2的物体用一倔强系数为K的轻弹簧相连放在光滑水平桌面上（如图），当两物体相距为x时，系统由静止释放，已知弹簧的自然长度为x0，当两物体相距为x0时，m1的速度大小为______________.

　２.Ａ物体以一定的动能Ek与静止的Ｂ物体发生完全非弹性碰撞，设mA=2mB，则碰后两物体的总动能为：

_______________.

　３.一弹簧变形量为x时，其恢复力为F=2ax-3bx2，现让该弹簧由x=0变形到x=L，其弹力的功为：

________________.

　４.两半径为r的光滑的匀质棋子，原为静止，相靠如图，现有另一半径为2r的同质料的大棋子以速度v0飞来，同它们碰撞，v0的方向正好在两小棋子中心连线的中垂线上，求弹性碰撞后大棋子的速度（大小棋子厚度相同，大棋子质量是小棋子的４倍）.

　５.两个质量分别为m1和m2的木块Ａ和Ｂ，用一个质量忽略不计，倔强系数为k的弹簧联接起来，放置在光滑水平面上，使Ａ紧靠墙壁，如图所示，用力推木块Ｂ使弹簧压缩x0，然后释放，已知m1=m，m2=3m，求

（1）释放后，Ａ、Ｂ两木块速度相等时的瞬时速度的大小；

（2）释放后，弹簧的最大伸长量.

６.在光滑水平面上放有一质量为M的三棱柱体，其上又放一质量为m的小三棱柱体，两柱体间的接触面光滑，三棱柱倾角为，开始时，两三棱柱相对静止.当小三棱柱沿大三棱柱斜面运动，在竖直方向下降h时，试证大三棱柱对地的速度为：

７*.如图，两小球A、B，质量分别为M和m，且m<

<

M，A球离地面高为h，今使两小球一起由静止下落，Ａ球落至地面时与地面发生弹性碰撞，碰撞后反弹，又与Ｂ球发生弹性碰撞，试求Ｂ球上升的高度（设两球直径都比h小得多，即d1<

h，d2<

h）.

第2-7守恒定律（习题课后作业）

１.传送带A以v0=2ms-1的速度把m=20kg的行李包送到坡道的上端，行李包沿光滑的坡道下滑后装到M=40kg的小车上（如图），已知小车与传送带之间的高度差h=0.6m，行李包与车板间的摩擦系数＝0.4，小车与地面的摩擦忽略不计，取g=10ms-2求：

（1）开始时行李包与车板间有相对滑动，当行李对小车相对静止时车的速度.

（2）从行李包送上小车到它相对于小车为静止时，所需的时间.

　２.质量m=0.10kg的小球，拴在长度L=0.5m的轻绳的一端，构成摆，摆动时与竖直的最大夹角为60°

.

（1）小球通过竖直位置时的速度为多少？

此时绳的张力？

（2）在<

60°

的任一位置，求小球速度v与的关系式，这时小球的加速度为何？

绳的张力为多大.

３.一个质量为M=10kg的物体放在光滑水平面上，并与一水平轻弹簧相连，如图，弹簧的倔强系数k=1000Nm-1，今有一质量为m=1kg的小球，以水平速度v0=4ms-1飞来，与物体M相撞后以v1=2ms-1的速度弹回.

（1）M起动后，弹簧将被压缩，弹簧可缩短多少？

（2）小球m和物体M的碰撞是弹性碰撞吗？

恢复系数多大？

（3）如果小球上涂的粘性物质，相撞后可与M粘在一起，则

（1）、

（2）所问结果又如何？

４.如图所示，两倔强系数为k1、k2的轻弹簧A、B串联后，在弹簧B下端挂一物体C，求此两弹簧的弹性势能的比值.