完整版关于一线三垂直模型及其在平面几何中的应用Word下载.docx

完整版关于一线三垂直模型及其在平面几何中的应用Word下载.docx

《完整版关于一线三垂直模型及其在平面几何中的应用Word下载.docx》由会员分享，可在线阅读，更多相关《完整版关于一线三垂直模型及其在平面几何中的应用Word下载.docx（11页珍藏版）》请在冰豆网上搜索。

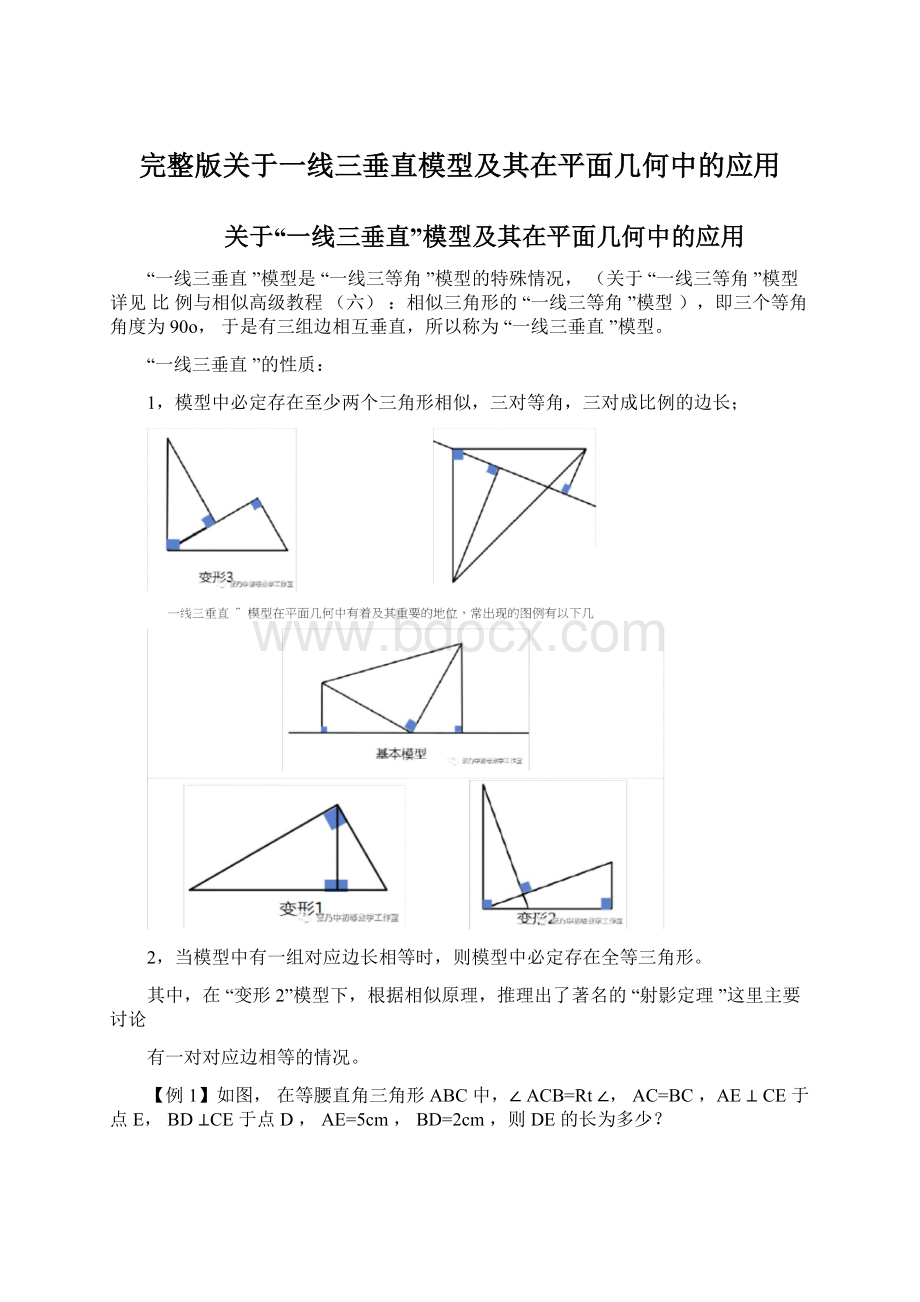
关于“一线三垂直”模型及其在平面几何中的应用

（二）

1，模型中必定存在至少两个三角形相似，三对等角，三对成比例的边长；

2，当模型中有一组对应边长相等时，则模型中必定存在全等三角形。

【例3】如图，在△ABC中，AB=AC，∠BAC=90o，分别过B，C向过A点的直线作垂线，垂足分别为E，F。

（1）如图1，过点A的直线与斜边BC不相交时，求证：

EF=EB+CF；

（2）如图2，过点A的直线与斜边BC相交时，其他条件不变，若BE=10，CF=3.求

EF的长。

【提示】

（1）图1是“一线三垂直”的基础模型，△ABE≌CAF；

（2）图2是“一线三垂直”的变形4，和【例1】相同。

【例4】如图，已知△AEB中，∠AEB=90o，以AB为边向外作正方形ABCD，连接AC、BD，交于点O，连接EO。

若BE=2，EO=3√2，求五边形AEBCD的面积。

解析】因为∠ABC=∠AEB=90o，故构造“一线三垂直”模型，如图。

过点C作CP⊥EB，交EB延长线于点P，连接OP。

则根据“一线三垂直”模型的性质，△AEB≌△BPC，∴BP=AE；

∵∠AOB=∠AEB=90o，

∴A、E、B、O四点共圆（详见“四点共圆”在解题中的妙用

（一）），∴∠BEO=∠BAO=45o；

同理∠BPO=∠BCO=45o，故△EOP为等腰直角三角形；

∵EO=3√2，∴EP=6，BP=4，

根据勾股定理，AB2=16+4=20，即S正方形ABCD=20，S△AEB=4×

2÷

2=4，∴S五边形AEBCD=20+4=24.

关于“一线三垂直”模型及其在平面几何中的应用（三）

【例5】已知△ABC中，∠ACB=90o，AC=BC，CD为AB边上的中线，点E为BC边上任意一点（不与A、D、B重合），BF⊥CE于点F，交CD于点G，AH⊥CE，

交CE延长线于点H，交CD延长线于点M。

（1）CG=AE；

（2）DE=DM。

（1）根据“一线三垂直”模型，△ACH≌△CBF，∴∠ACE=∠CBG，又∠CAE=∠BCG=45o，AC=BC，∴△ACE≌△BCG；

（2）由“一线三垂直”模型可知，∠ACE=∠CBG，BF=CH，∴∠HCM=∠FBE，又∠BFE=∠CHM=90o，

∴△CHM≌△BFE，BE=CM，从而DE=DM。

同时我们也应该注意到：

△ACM≌△CBE；

△ADM≌△CDE≌△BDG；

△AHE≌△CFG；

DM=DG=DE；

△GEM为等腰直角三角形等。

构造“一线三垂直”模型，是作辅助线常用的一种手段。

例6】如图，直线l1∥l2∥l3，且l1到l2的距离为3，l2到l3的距离为4，等腰直

B分别在l1、l3上。

求△ABC的面积。

和l3于点D、E，构造“一线三垂直”模型，

关于“一线三垂直”模型及其在平面几何中的应用（四）

【例7】

（2018初二希望杯练习题）如图，四边形ABCD为直角梯形，AD∥BC，∠BCD=90o，AB=BC+AD，∠DAC=45o，E为CD上一点，且∠BAE=45o，若CD=4，求△ABE的面积。

【解析】如图，过点E作EG⊥AE，交AB延长线于点G，过点G作GH⊥DC，交DC延长线于点H，构造“一线三垂直”模型；

过点G作GK⊥BC于点K，过点B作BF⊥AD于点F。

则△ADE≌△EHG，DE=GH；

AD=EH=CD，

∴DE=CH，故四边形CKGH为正方形。

AF=4-BC，AB=4+BC，BF=4，

∴（4+BC）2=（4-BC）2+42，解得：

BC=1，所以AB=5；

设DE=x，则BK=1-x，GK=x，AE2=x2+42

∵△AEG为等腰直角三角形，∴AG2=2AE2，

（5+BG）2=2（x2+42），将BG代入，化简得：

（7x-4）2=0，x=4/7，

∴△ABE面积=梯形ABCD面积-△ADE面积-△BCE面积

=（1+4）×

4÷

2-4×

4/7÷

2-1×

（4-4/7）2÷

=50/7。

在直角坐标系中构造“一线三垂直”模型，是解决坐标问题的一种有效手段。

【例8】如图，在直角坐标系中，点A（1，2），点B（0，-1），已知△ABC为等腰

直角三角形，求点C的坐标。

【解析】设C（m，p）。

（1）当∠BAC为直角时：

①当点C在AB右侧时，如图1。

过点A作DE∥x轴，交y轴于点D，过点C作CE⊥DE于点E。

根据“一线三垂直”模型，△ABD≌△ACE，

∴DB=AE，CE=DA，即：

m-1=3，2-p=1，解得：

m=4，p=1，∴C（4，1）；

②当点C在AB左侧时，如图2。

过点A作DE∥x轴，交y轴于点D，过点C作CE⊥DE

于点E。

根据“一线三垂直”模型，△ABD≌△ACE，∴DB=AE，CE=DA，即：

1-m=3，p-2=1，解得：

m=-2，p=3，∴C（-2，3）；

（或者用下列方法：

此时，点C和①中的C关于点A对称，故m=2×

1-4=-2，p=2×

2－1=3.）

（2）当∠ABC为直角时：

①当点C在AB右侧时，如图3。

过点A作AE∥x轴，交y轴于点E，过点C作CD⊥y轴于点D。

根据“一线三垂直”模型，△ABE≌△BCD，∴DB=AE，BE=CD，即：

-1-p=1，m=3，解得：

m=3，p=-2，∴C（3，-2）；

②当点C在AB左侧时，如图4。

过点B作DE∥x轴，过点C作CD⊥DE于点D，过点A作AE⊥DE于点E。

根据“一线三垂直”模型，△ABE≌△BCD，

∴BE=CD，BD=AE，即：

0-m=3，p-（-1）=1，

解得：

m=-3，p=0，∴C（-3，0）；

此时，点C和①中的C关于点B对称，故m=2×

0-3=-3，p=-1×

2－（-2）=0.）

（3）当∠ACB为直角时：

①当点C在AB右侧时，如图5。

过点C作CD∥x轴，过点A作AD⊥CD于点D，CD交y轴于点E。

根据“一线三垂直”模型，△ACD≌△CBE，

∴BE=CD，CE=DA，即：

m=2-p，p-（-1）=m-1，解得：

m=2，p=0，即CD与x轴重合，点E与O重合，

∴C（2，0）；

②当点C在AB左侧时，如图6。

1-m=p-（-1），2-p=0-m，解得：

m=-1，p=1，∴C（-1，1）。

此时，点C和①中的C关于AB的中点对称，AB的中点坐标为（0.5，0.5），故m=2×

0.5-2=-1，p=0.5×

2－0=1.）

综上所述：

符合条件的点C的坐标有6个：

（4，1）；

（-2，3）；

（3，-2）；

（-3，0）；

（2，0）；

（-1，1）。

关于“一线三垂直”模型及其在平面几何中的应用（五）

前面讨论的是关于“一线三垂直模型”有两条边相等时的情况。

如果不存在两条边相等，那么“一线三垂直模型”的性质是必然存在一对或几对相似三角形，这个性质在初中平面几何中的应用也是十分广泛，尤其在直角坐标系中的函数图像与平面几何的综合应用题或压轴题经常得到应用，也是作辅助线的思想方法。

经常出现的图例跟前面介绍的一样（关于“一线三垂直”模型及其在平面几何中的应用

（一）），只是直角的两条边不一定相等。

A（1，3），点B（2，-1），坐标轴上是否存在请求出点C的坐标；

若不存在，请说明理由。

∴AD∶CE=CD∶BE，即：

1∶（c+1）=（3-c）∶2，解得：

c1=1+√2，c2=1-√2，

故C（0，1+√2）；

或C（0，1-√2）；

2）当点C在x轴上时：

如图2，设C（c，0），分别过点A、B作y轴的平行线，交x轴于点D、E。

则根据“一线三垂直模型”，△ACD∽△CBE，

∴AD∶CE=CD∶BE，即：

3∶（2-c）=（1-c）∶2，

或3∶（c-2）=（c-1）∶2，

综上所述，符合条件的点C的坐标有4个，分别为：

（0，1+√2）；

（0，1-√2）；

【例10】如图，在直角坐标系中，点A（1，3），点B（2，-1），在一次函数y=x/2-1

的图像上是否存在点C，使得∠ACB为直角？

若存在，请求出点C的坐标；

若不存

在，请说明理由。

解析】设∠ACB为直角时，点C（c，c/2-1），

如图1，过点C作y轴的平行线DE，分别过点A、B作DE的垂线，垂足分别为D、

E。

由“一线三垂直模型”可知：

△ACD∽△CBE，

（c-1）∶（（c/2-1）+1）=（3-（c/2-1））∶（c-2），化简得：

5c2-20c+8=0，解得：