人教版七年级数学下《压轴题培优》期末复习专题含答案Word格式文档下载.docx

人教版七年级数学下《压轴题培优》期末复习专题含答案Word格式文档下载.docx

《人教版七年级数学下《压轴题培优》期末复习专题含答案Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《人教版七年级数学下《压轴题培优》期末复习专题含答案Word格式文档下载.docx（18页珍藏版）》请在冰豆网上搜索。

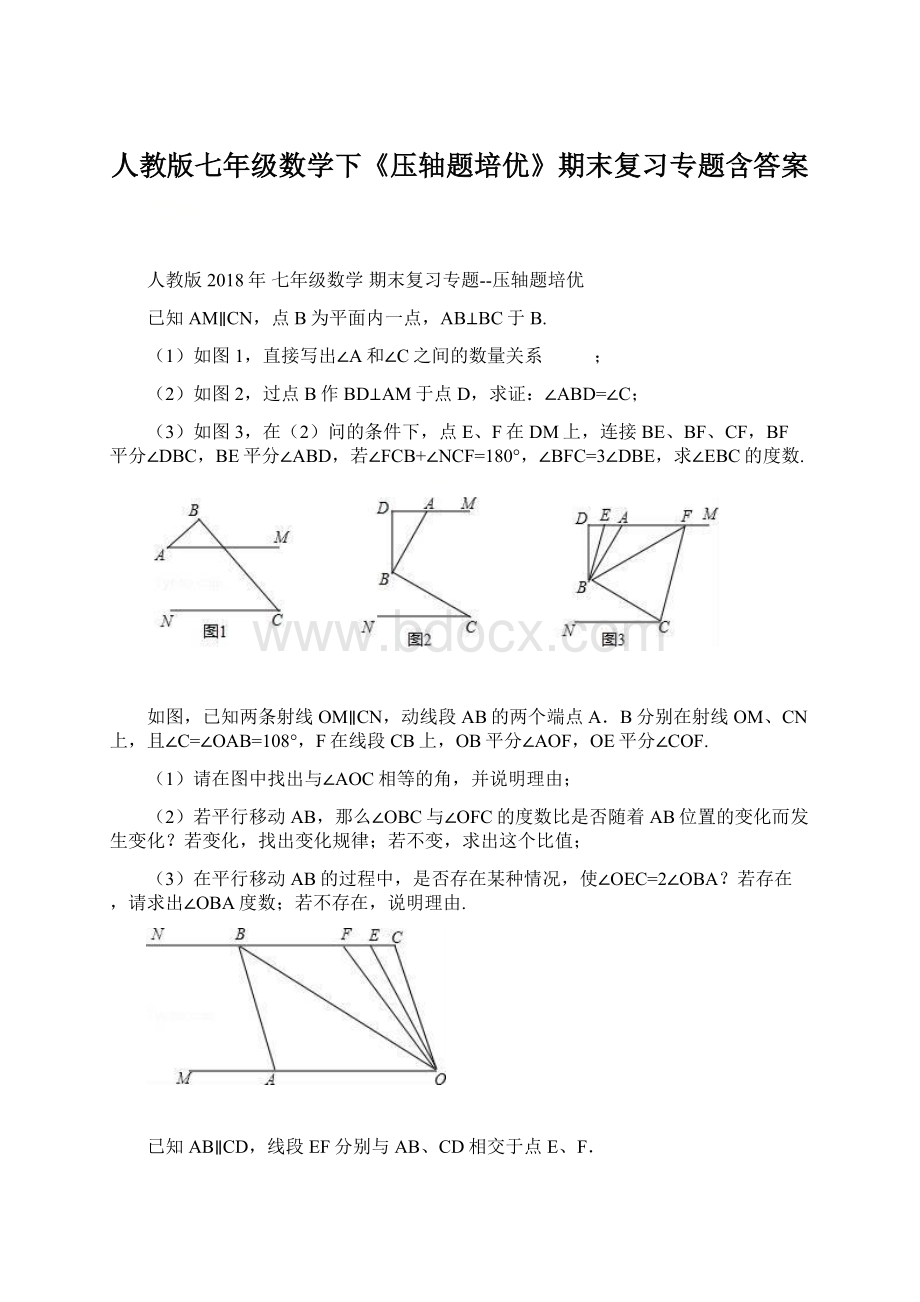
如果不成立，试探究它们之间新的相等关系并证明．

如图1,在平面直角坐标系中,A（a,0）是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B（0,b）,且（a-3）2+|b+4|=0,S四边形AOBC=16．

（1）求C点坐标；

（2）如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数．

（3）如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化？

若不变,求出其值,若变化,说明理由．

已知BC∥OA,∠B=∠A=100°

.试回答下列问题：

（1）如图1所示,求证：

OB∥AC；

（2）如图2,若点E、F在BC上,且满足∠FOC=∠AOC，并且OE平分∠BOF.试求∠EOC的度数；

（3）在

（2）的条件下，若平行移动AC，如图3，那么∠OCB：

∠OFB的值是否随之发生变化？

若变化，试说明理由；

若不变，求出这个比值。

如图，已知AM//BN，∠A=600.点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D.

（1）①∠ABN的度数是；

②∵AM//BN，∴∠ACB=∠；

（2）求∠CBD的度数；

（3）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？

若不变化，请写出它们之间的关系，并说明理由；

若变化，请写出变化规律.

（4）当点P运动到使∠ACB=∠APD时，∠ABC的度数是.

课题学习：

平行线的“等角转化”功能．阅读理解：

如图1，已知点A是BC外一点，连接AB，AC．求∠BAC+∠B+∠C的度数．

（1）阅读并补充下面推理过程．

解：

过点A作ED∥BC，所以∠B=，∠C=．

又因为∠EAB+∠BAC+∠DAC=180°

．

所以∠B+∠BAC+∠C=180°

解题反思：

从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决．

方法运用：

（2）如图2,已知AB∥ED，求∠B+∠BCD+∠D的度数．

深化拓展：

（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°

，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．

请从下面的A，B两题中任选一题解答，我选择题．

A．如图3，点B在点A的左侧，若∠ABC=60°

，则∠BED的度数为°

B．如图4,点B在点A的右侧,且AB＜CD，AD＜BC.若∠ABC=n°

，则∠BED度数为°

．（用含n的代数式表示）

已知A（0，a），B（b，0），a、b满足

.

（1）求a、b的值；

（2）在坐标轴上找一点D，使三角形ABD的面积等于三角形OAB面积的一半，求D点坐标；

（3）做∠BAO平分线与∠AOC平分线BE的反向延长线交于P点，求∠P的度数.

如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）2+b-2=0，过C作CB⊥x轴于B．

（1）求△ABC的面积．

（2）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．

（3）在y轴上是否存在点P，使得△ABC和△ACP的面积相等？

若存在，求出P点坐标；

若不存在，请说明理由.

如图1，在平面直角坐标系中，点A为x轴负半轴上一点，点B为x轴正半轴上一点，C（0，a），D（b，a），其中a，b满足关系式：

|a+3|+（b-a+1）2=0.

（1）a=，b=，△BCD的面积为；

（2）如图2，若AC⊥BC，点P线段OC上一点，连接BP，延长BP交AC于点Q，当∠CPQ=∠CQP时，求证:

BP平分∠ABC；

（3）如图3，若AC⊥BC，点E是点A与点B之间一动点，连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时，

的值是否变化？

若不变，求出其值；

若变化，请说明理由.

如图1，在平面直角坐标系中，A（a，0），B（b，3），C（4，0），且满足（a+b）2+|a-b+6|=0，线段AB交y轴于F点．

（1）求点A．B的坐标．

（2）点D为y轴正半轴上一点，若ED∥AB，且AM，DM分别平分∠CAB，∠ODE，如图2，

求∠AMD的度数．

（3）如图3，（也可以利用图1）

①求点F的坐标；

②点P为坐标轴上一点，若△ABP的三角形和△ABC的面积相等？

若存在，求出P点坐标．

如图所示，A（1，0）,点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为（-3，2）．

（1）直接写出点E的坐标；

（2）在四边形ABCD中，点P从点B出发，沿“BC→CD”移动．若点P的速度为每秒1个单位长度，运动时间为t秒，回答下列问题：

①当t=秒时，点P的横坐标与纵坐标互为相反数；

②求点P在运动过程中的坐标，（用含t的式子表示，写出过程）；

③当3秒＜t＜5秒时，设∠CBP=x°

，∠PAD=y°

，∠BPA=z°

，试问x，y，z之间的数量关系能否确定？

若能，请用含x，y的式子表示z，写出过程；

若不能，说明理由．

如图，已知平面直角坐标系内A（2a-1，4）,B（-3，3b+1），A．B;

两点关于y轴对称.

（1）求A．B的坐标;

（2）动点P、Q分别从A点、B点同时出发，沿直线AB向右运动，同向而行，点的速度是每秒2个单位长度，Q点的速度是每秒4个单位长度，设P、Q的运时间为t秒，用含t的代数式表示三角形OPQ的面积S，并写出t的取值范围;

（3）在平面直角坐标系中存在一点M，点M的横纵坐标相等，且满足S△PQM：

S△OPQ=3:

2，求出点M的坐标，并求出当S△AQM=15时，三角形OPQ的面积.

如图，在平面直角坐标系中，O为原点，点A（0，8），点B（m，0），且m＞0.把△AOB绕点A逆时针旋转90°

，得△ACD，点O，B旋转后的对应点为C，D.

（1）点C的坐标为；

（2）①设△BCD的面积为S，用含m的式子表示S，并写出m的取值范围；

②当S=6时，求点B的坐标（直接写出结果即可）.

如图，已知在平面直角坐标系中，△ABO的面积为8,OA=OB,BC=12，点P的坐标是（a,6）.

（1）求△ABC三个顶点A,B,C的坐标;

（2）若点P坐标为（1,6），连接PA,PB，则△PAB的面积为;

（3）是否存在点P，使△PAB的面积等于△ABC的面积?

如果存在，请求出点P的坐标.

参考答案

⑴∠C=45°

分⑵∠C=∠APC-∠A（证明略）⑶不成立，新的相等关系为∠C=∠APC+∠A（证明略）

（1）∵（a﹣3）2+|b+4|=0，∴a﹣3=0，b+4=0，

∴a=3，b=﹣4，∴A（3，0），B（0，﹣4），∴OA=3，OB=4，

∵S四边形AOBC=16．∴0.5（OA+BC）×

OB=16，∴0.5（3+BC）×

4=16，∴BC=5，

∵C是第四象限一点，CB⊥y轴，∴C（5，﹣4）

（2）如图，

延长CA，∵AF是∠CAE的角平分线，∴∠CAF=0.5∠CAE，

∵∠CAE=∠OAG，∴∠CAF=0.5∠OAG，

∵AD⊥AC，∴∠DAO+∠OAG=∠PAD+∠PAG=90°

，

∵∠AOD=90°

，∴∠DAO+∠ADO=90°

，∴∠ADO=∠OAG，∴∠CAF=0.5∠ADO，

∵DP是∠ODA的角平分线∴∠ADO=2∠ADP，∴∠CAF=∠ADP，

∵∠CAF=∠PAG，∴∠PAG=∠ADP，

∴∠APD=180°

﹣（∠ADP+∠PAD）=180°

﹣（∠PAG+∠PAD）=180°

﹣90°

=90°

即：

∠APD=90°

（3）不变，∠ANM=45°

理由：

如图，

，∴∠ADO+∠DAO=90°

∵DM⊥AD，∴∠ADO+∠BDM=90°

，∴∠DAO=∠BDM，

∵NA是∠OAD的平分线，∴∠DAN=0.5∠DAO=0.5∠BDM，

∵CB⊥y轴，∴∠BDM+∠BMD=90°

，∴∠DAN=0.5（90°

﹣∠BMD），

∵MN是∠BMD的角平分线，∴∠DMN=0.5∠BMD，

∴∠DAN+∠DMN=0.5（90°

﹣∠BMD）+0.5∠BMD=45°

在△DAM中，∠ADM=90°

，∴∠DAM+∠DMA=90°

在△AMN中，

∠ANM=180°

﹣（∠NAM+∠NMA）

=180°

﹣（∠DAN+∠DAM+∠DMN+∠DMA）

﹣[（∠DAN+DMN）+（∠DAM+∠DMA）]

﹣（45°

+90°

）=45°

∴D点在运动过程中，∠N的大小不变，求出其值为45°

略

（1）120°

；

∠CBN

（2）∵AM∥BN，

∴∠ABN+∠A=180°

∴∠ABN=180°

-60°

=120°

∴∠ABP+∠PBN=120°

∵BC平分∠ABP，BD平分∠PBN，

∴∠ABP=2∠CBP，∠PBN=2∠DBP，

∴2∠CBP+2∠DBP=120°

∴∠CBD=∠CBP+∠DBP=60°

（3）不变，∠APB：

∠ADB=2：

1．

∵AM∥BN，

∴∠APB=∠PBN，∠ADB=∠DBN，

∵BD平分∠PBN，

∴∠PBN=2∠DBN，

∴∠APB：

1；

（4）∵AM∥BN，

∴∠ACB=∠CBN，

当∠ACB=∠ABD时，则有∠CBN=∠ABD，

∴∠ABC+∠CBD=∠CBD+∠DBN，

∴∠ABC=∠DBN，

由

（1）可知∠ABN=120°

，∠CBD=60°

∴∠ABC+∠DBN=60°

∴∠ABC=30°

（1）∵ED∥BC，∴∠B=∠EAD，∠C=∠DAE，故答案为：

∠EAD，∠DAE；

（2）过C作CF∥AB，∵AB∥DE，∴CF∥DE，∴∠D=∠FCD，

∵CF∥AB，∴∠B=∠BCF，∵∠BCF+∠BCD+∠DCF=360°

，∴∠B+∠BCD+∠D=360°

（3）A．如图2，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，

∴∠ABE=∠BEF，∠CDE=∠DEF，

∵BE平分∠ABC，DE平分∠ADC，∠ABC=60°

，∠ADC=70°

∴∠ABE=

∠ABC=30°

，∠CDE=

∠ADC=35°

∴∠BED=∠BEF+∠DEF=30°

+35°

=65°

故答案为：

65；

B、如图3，过点E作EF∥AB，

∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°

∠ABC=

n°

∵AB∥CD，∴AB∥CD∥EF，∴∠BEF=180°

﹣∠ABE=180°

﹣

，∠CDE=∠DEF=35°

∴∠BED=∠BEF+∠DEF=180°

=215°

．故答案为：

215°

n．

（1）a=-4，b=8；

（2）D（-6,0）,（-2,0）,（0,4）,（0,12）；

（3）45°

（1）根据题意，可得三角形OAB沿x轴负方向平移3个单位得到三角形DEC，

∵点A的坐标是（1，0），∴点E的坐标是（-2，0）；

（-2，0）；

（2）①∵点C的坐标为（-3，2）．∴BC=3，CD=2，

∵点P的横坐标与纵坐标互为相反数；

∴点P在线段BC上，∴PB=CD，即t=2；

∴当t=2秒时，点P的横坐标与纵坐标互为相反数；

2；

②当点P在线段BC上时，点P的坐标（-t，2），

当点P在线段CD上时，点P的坐标（-3，5-t）；

③能确定，如图，过P作PE∥BC交AB于E，则PE∥AD，∴∠1=∠CBP=x°

，∠2=∠DAP=y°

，∴∠BPA=∠1+∠2=x°

+y°

=z°

，∴z=x+y．

（1）∵点A（0，8），∴AO=8，

∵△AOB绕点A逆时针旋转90°

得△ACD，∴AC=AO=8，∠OAC=90°

，∴C（8，8），

（8，8）；

（2）①延长DC交x轴于点E，∵点B（m，0），∴OB=m，

得△ACD，

∴DC=OB=m，∠ACD=∠AOB=90°

，∠OAC=90°

，∴∠ACE=90°

∴四边形OACE是矩形，∴DE⊥x主，OE=AC=8，

分三种情况：

a、当点B在线段OE的延长线上时，如图1所示：

则BE=OB﹣OE=m﹣8，∴S=0.5DC•BE=0.5m（m﹣8），即S=0.5m2﹣4m（m＞8）；

b、当点B在线段OE上（点B不与O，E重合）时，如图2所示：

则BE=OE﹣OB=8﹣m，∴S=0.5DC•BE=0.5m（8﹣m），即S=﹣0.5m2+4m（0＜m＜8）；

c、当点B与E重合时，即m=8，△BCD不存在；

综上所述，S=0.5m2﹣4m（m＞8），或S=﹣0.5m2+4m（0＜m＜8）；

②当S=6，m＞8时，0.5m2﹣4m=6，解得：

m=4±

2

（负值舍去），∴m=4+2

当S=6，0＜m＜8时，﹣0.5m2+4m=6，解得：

m=2或m=6，

∴点B的坐标为（4+2

，0）或（2，0）或（6，0）.