咸宁市中考数学《全等三角形》经典培优题含答案Word文档下载推荐.docx

咸宁市中考数学《全等三角形》经典培优题含答案Word文档下载推荐.docx

《咸宁市中考数学《全等三角形》经典培优题含答案Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《咸宁市中考数学《全等三角形》经典培优题含答案Word文档下载推荐.docx（12页珍藏版）》请在冰豆网上搜索。

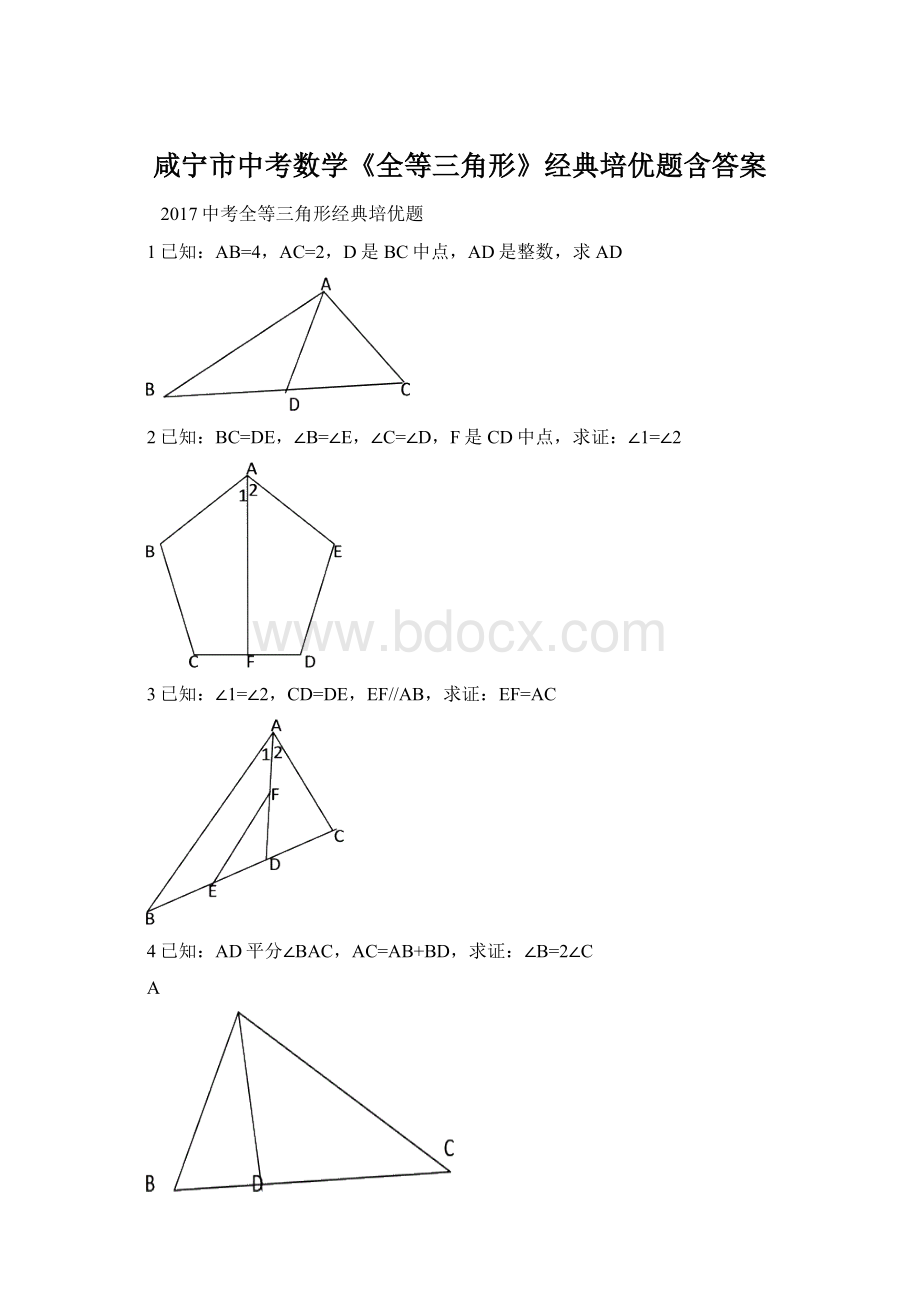
8.P是∠BAC平分线AD上一点，AC>

AB，求证：

PC-PB<

AC-AB

9已知，E是AB中点，AF=BD，BD=5，AC=7，求DC

10．如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：

AD+BC=AB．

11如图，△ABC中，AD是∠CAB的平分线，且AB=AC+CD，求证：

∠C=2∠B

12如图：

AE、BC交于点M，F点在AM上，BE∥CF，BE=CF。

AM是△ABC的中线。

13已知：

如图，AB=AC，BDAC，CEAB，垂足分别为D、E，BD、CE相交于点F。

BE=CD．

14在△ABC中，

，

，直线

经过点

，且

于

.

（1）当直线

绕点

旋转到图1的位置时，

①

≌

；

②

（2）当直线

旋转到图2的位置时，

（1）中的结论还成立吗？

若成立，请给出证明；

若不成立，说明理由.

15如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC。

（1）EC=BF；

（2）EC⊥BF

16．如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD相等吗？

请说明理由

17．如图9所示，△ABC是等腰直角三角形，∠ACB＝90°

，AD是BC边上的中线，过C作AD的垂线，交AB于点E，交AD于点F，求证：

∠ADC＝∠BDE．

全等三角形证明经典（答案）

1.延长AD到E,使DE=AD,

则三角形ADC全等于三角形EBD

即BE=AC=2在三角形ABE中,AB-BE<

AE<

AB+BE

即:

10-2<

2AD<

10+24<

AD<

6

又AD是整数,则AD=5

2证明：

连接BF和EF。

因为BC=ED,CF=DF,∠BCF=∠EDF。

所以三角形BCF全等于三角形EDF（边角边）。

所以BF=EF,∠CBF=∠DEF。

连接BE。

在三角形BEF中,BF=EF。

所以∠EBF=∠BEF。

又因为∠ABC=∠AED。

所以∠ABE=∠AEB。

所以AB=AE。

在三角形ABF和三角形AEF中，

AB=AE,BF=EF,

∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。

所以三角形ABF和三角形AEF全等。

所以∠BAF=∠EAF（∠1=∠2）。

3证明：

过E点，作EG//AC，交AD延长线于G

则∠DEG=∠DCA，∠DGE=∠2

又∵CD=DE

∴⊿ADC≌⊿GDE（AAS）

∴EG=AC

∵EF//AB

∴∠DFE=∠1

∵∠1=∠2

∴∠DFE=∠DGE

∴EF=EG

∴EF=AC

4证明：

在AC上截取AE=AB，连接ED

∵AD平分∠BAC

∴∠EAD=∠BAD

又∵AE=AB，AD=AD

∴⊿AED≌⊿ABD（SAS）

∴∠AED=∠B，DE=DB

∵AC=AB+BD

AC=AE+CE

∴CE=DE

∴∠C=∠EDC

∵∠AED=∠C+∠EDC=2∠C

∴∠B=2∠C

5证明：

在AE上取F，使EF＝EB，连接CF

因为CE⊥AB

所以∠CEB＝∠CEF＝90°

因为EB＝EF，CE＝CE，

所以△CEB≌△CEF

所以∠B＝∠CFE

因为∠B＋∠D＝180°

，∠CFE＋∠CFA＝180°

所以∠D＝∠CFA

因为AC平分∠BAD

所以∠DAC＝∠FAC

又因为AC＝AC

所以△ADC≌△AFC（SAS）

所以AD＝AF

所以AE＝AF＋FE＝AD＋BE

6证明:

在BC上截取BF=BA,连接EF.

∠ABE=∠FBE,BE=BE,则⊿ABE≌ΔFBE（SAS）,∠EFB=∠A;

AB平行于CD,则:

∠A+∠D=180°

;

又∠EFB+∠EFC=180°

则∠EFC=∠D;

又∠FCE=∠DCE,CE=CE,故⊿FCE≌ΔDCE（AAS）,FC=CD.

所以,BC=BF+FC=AB+CD.

7证明：

设线段AB,CD所在的直线交于E，（当AD<

BC时，E点是射线BA,CD的交点，当AD>

BC时，E点是射线AB,DC的交点）。

则：

△AED是等腰三角形。

所以：

AE=DE

而AB=CD

BE=CE（等量加等量，或等量减等量）

△BEC是等腰三角形

角B=角C.

8作B关于AD的对称点B‘，因为AD是角BAC的平分线，B'

在线段AC上（在AC中间，因为AB较短）

因为PC<

PB’+B‘C,PC-PB’<

B‘C,而B'

C=AC-AB'

=AC-AB,所以PC-PB<

9作AG∥BD交DE延长线于G

AGE全等BDE

AG=BD=5

AGF∽CDF

AF=AG=5

所以DC=CF=2

10证明：

做BE的延长线，与AP相交于F点，

∵PA//BC

∴∠PAB+∠CBA=180°

又∵，AE，BE均为∠PAB和∠CBA的角平分线

∴∠EAB+∠EBA=90°

∴∠AEB=90°

，EAB为直角三角形

在三角形ABF中，AE⊥BF，且AE为∠FAB的角平分线

∴三角形FAB为等腰三角形，AB=AF,BE=EF

在三角形DEF与三角形BEC中，

∠EBC=∠DFE,且BE=EF，∠DEF=∠CEB，

∴三角形DEF与三角形BEC为全等三角形，∴DF=BC

∴AB=AF=AD+DF=AD+BC

11证明：

在AB上找点E，使AE=AC

∵AE=AC，∠EAD=∠CAD，AD=AD

∴△ADE≌△ADC。

DE=CD，∠AED=∠C

∵AB=AC+CD，∴DE=CD=AB-AC=AB-AE=BE

∠B=∠EDB

∠C=∠B+∠EDB=2∠B

12证明：

∵BE‖CF

∴∠E=∠CFM，∠EBM=∠FCM

∵BE=CF

∴△BEM≌△CFM

∴BM=CM

∴AM是△ABC的中线.

13证明：

因为AB=AC，

所以∠EBC=∠DCB

因为BD⊥AC，CE⊥AB

所以∠BEC=∠CDB

BC=CB（公共边）

则有三角形EBC全等于三角形DCB

所以BE＝CD

14

（1）证明：

∵∠ACB=90°

∴∠ACD+∠BCE=90°

而AD⊥MN于D，BE⊥MN于E，

∴∠ADC=∠CEB=90°

，∠BCE+∠CBE=90°

∴∠ACD=∠CBE．

在Rt△ADC和Rt△CEB中，{∠ADC=∠CEB∠ACD=∠CBEAC=CB，

∴Rt△ADC≌Rt△CEB（AAS），

∴AD=CE，DC=BE，

∴DE=DC+CE=BE+AD；

（2）不成立，证明：

在△ADC和△CEB中，{∠ADC=∠CEB=90°

∠ACD=∠CBEAC=CB，

∴△ADC≌△CEB（AAS），

∴DE=CE-CD=AD-BE；

15

（1）证明;

因为AE垂直AB

所以角EAB=角EAC+角CAB=90度

因为AF垂直AC

所以角CAF=角CAB+角BAF=90度

所以角EAC=角BAF

因为AE=ABAF=AC

所以三角形EAC和三角形FAB全等

所以EC=BF

角ECA=角F

（2）延长FB与EC的延长线交于点G

因为角ECA=角F（已证）

所以角G=角CAF

因为角CAF=90度

所以EC垂直BF

16在AB上取点N,使得AN=AC

∠CAE=∠EAN,AE为公共边,所以三角形CAE全等三角形EAN

所以∠ANE=∠ACE

又AC平行BD

所以∠ACE+∠BDE=180

而∠ANE+∠ENB=180

所以∠ENB=∠BDE

∠NBE=∠EBN

BE为公共边,

所以三角形EBN全等三角形EBD

所以BD=BN

所以AB=AN+BN=AC+BD

17证明：

作CG平分∠ACB交AD于G

∴∠ACG=∠DCG=45°

AC=BC

∴∠B=∠BAC=45°

∴∠B=∠DCG=∠ACG

∵CF⊥AD

∴∠ACF+∠DCF=90°

∵∠ACF+∠CAF=90°

∴∠CAF=∠DCF

∵AC=CB∠ACG=∠B

∴△ACG≌△CBE

∴CG=BE

∵∠DCG=∠BCD=BD

∴△CDG≌△BDE

∴∠ADC=∠BDE