统计学期末大作业题目及答案.docx
《统计学期末大作业题目及答案.docx》由会员分享,可在线阅读,更多相关《统计学期末大作业题目及答案.docx(57页珍藏版)》请在冰豆网上搜索。
统计学期末大作业题目及答案
统计学实践作业
参数估计练习题
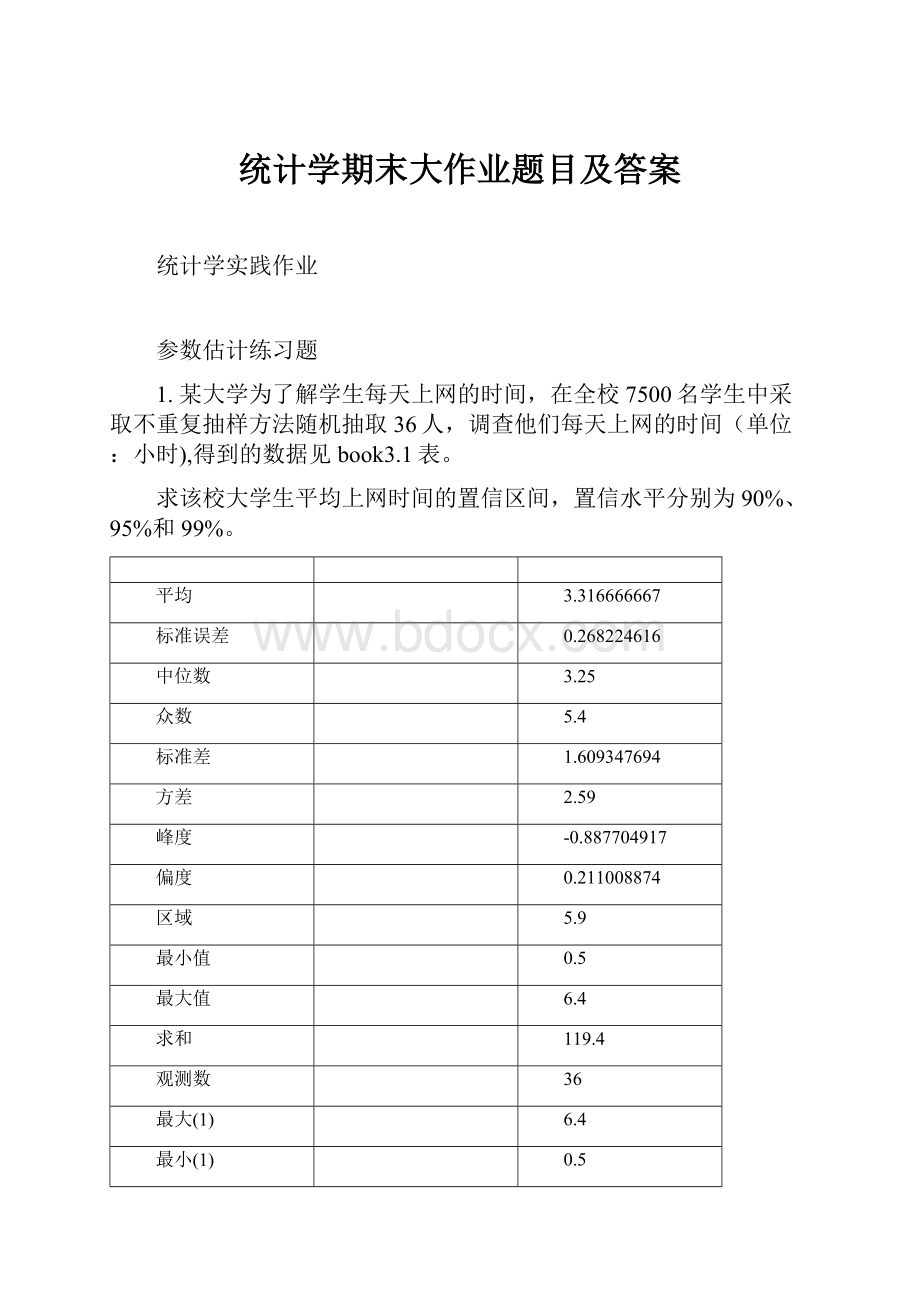
1.某大学为了解学生每天上网的时间,在全校7500名学生中采取不重复抽样方法随机抽取36人,调查他们每天上网的时间(单位:
小时),得到的数据见book3.1表。
求该校大学生平均上网时间的置信区间,置信水平分别为90%、95%和99%。
平均
3.316666667
标准误差
0.268224616
中位数
3.25
众数
5.4
标准差
1.609347694
方差
2.59
峰度
-0.887704917
偏度
0.211008874
区域
5.9
最小值
0.5
最大值
6.4
求和
119.4
观测数
36
最大
(1)
6.4
最小
(1)
0.5
置信度(90.0%)
0.453184918
置信区间
2.863481748
3.769851585
平均
3.316666667
标准误差
0.268224616
中位数
3.25
众数
5.4
标准差
1.609347694
方差
2.59
峰度
-0.887704917
偏度
0.211008874
区域
5.9
最小值
0.5
最大值
6.4
求和
119.4
观测数
36
最大
(1)
6.4
最小
(1)
0.5
置信度(95.0%)
0.544524915
置信区间
2.772141751
3.861191582
平均
3.316666667
标准误差
0.268224616
中位数
3.25
众数
5.4
标准差
1.609347694
方差
2.59
峰度
-0.887704917
偏度
0.211008874
区域
5.9
最小值
0.5
最大值
6.4
求和
119.4
观测数
36
最大
(1)
6.4
最小
(1)
0.5
置信度(99.0%)
0.730591706
置信区间
2.58607496
4.047258373
2.某机器生产的袋茶重量(g)的数据见book3.2。
构造其平均重量的置信水平为90%、95%和99%的置信区间。
平均
3.32952381
标准误差
0.05272334
中位数
3.25
众数
3.2
标准差
0.241608696
方差
0.058374762
峰度
0.413855703
偏度
0.776971476
区域
0.95
最小值
2.95
最大值
3.9
求和
69.92
观测数
21
最大
(1)
3.9
最小
(1)
2.95
置信度(90.0%)
0.090932905
置信区间
3.238590905
3.420456714
平均
3.32952381
标准误差
0.05272334
中位数
3.25
众数
3.2
标准差
0.241608696
方差
0.058374762
峰度
0.413855703
偏度
0.776971476
区域
0.95
最小值
2.95
最大值
3.9
求和
69.92
观测数
21
最大
(1)
3.9
最小
(1)
2.95
置信度(95.0%)
0.109978959
置信区间
3.21954485
3.439502769
平均
3.32952381
标准误差
0.05272334
中位数
3.25
众数
3.2
标准差
0.241608696
方差
0.058374762
峰度
0.413855703
偏度
0.776971476
区域
0.95
最小值
2.95
最大值
3.9
求和
69.92
观测数
21
最大
(1)
3.9
最小
(1)
2.95
置信度(99.0%)
0.150015812
置信区间
3.179507997
3.479539622
3.某机器生产的袋茶重量(g)的数据见book3.3。
构造其平均重量的置信水平为90%、95%和99%的置信区间。
平均
3.29
标准误差
0.014798365
中位数
3.29
众数
3.3
标准差
0.087548306
方差
0.007664706
峰度
1.781851265
偏度
0.003904912
区域
0.47
最小值
3.05
最大值
3.52
求和
115.15
观测数
35
最大
(1)
3.52
最小
(1)
3.05
置信度(90.0%)
0.025022913
置信区间
3.264977087
3.315022913
平均
3.29
标准误差
0.014798365
中位数
3.29
众数
3.3
标准差
0.087548306
方差
0.007664706
峰度
1.781851265
偏度
0.003904912
区域
0.47
最小值
3.05
最大值
3.52
求和
115.15
观测数
35
最大
(1)
3.52
最小
(1)
3.05
置信度(95.0%)
0.030073895
置信区间
3.259926105
3.320073895
平均
3.29
标准误差
0.014798365
中位数
3.29
众数
3.3
标准差
0.087548306
方差
0.007664706
峰度
1.781851265
偏度
0.003904912
区域
0.47
最小值
3.05
最大值
3.52
求和
115.15
观测数
35
最大
(1)
3.52
最小
(1)
3.05
置信度(99.0%)
0.040375775
置信区间
3.249624225
3.330375775
资料整理练习题
1.为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:
A.好;B.较好;C.一般;D.差;E.较差。
调查结果见表book1.1。
要求:
(1)制作一张频数分布表;
(2)绘制统计图,反映评价等级的分布。
计数项:
xt
xt
汇总
A
14
B
21
C
32
D
18
E
15
(空白)
总计
100
2.某行业管理局所属40个企业2002年的产品销售收入数据(单位:
万元)见book1.2。
要求:
(1)根据销售收入在125万元以上为先进企业,115~125万元为良好企业,105~115万元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业进行分组,编制频数分布表,并计算出累积频数和累积频率;
累计频数
累计频率
-104
9
22.50%
105-114
9
45.00%
115-124
11
72.50%
125+
11
100.00%
(2)绘制统计图,反映分布情况。
3.北方某城市1月~2月份各天气温的记录数据见book1.3。
(1)对上面的数据进行适当的分组。
(2)绘制统计图,说明该城市气温分布的特点.
接收
频率
累积%
-10
26
40.00%
-5
15
63.08%
0
15
86.15%
5
5
93.85%
10
4
100.00%
其他
0
100.00%
说明:
该城市气温在逐步回暖,整体偏冷。
多变量资料整理练习题
下面是有关“北京地区大学生掌上阅读状况调查”的部分题目,
(1)性别:
1男2女
(2)学级:
1大专2大一3大二4大三5大四6研一
7研二8博士生
(3)月生活费:
1600元以下2600—1000元31000—1500元
41500—2000元52000元以上
(4)手机类型:
1低端机2中端机3高端机4智能机5其他
(5)运营商:
1中国移动2中国联通3中国电信4中国网通
被调查者对这5个题目的回答如数据表book1.8。
1.分析不同性别学生选择手机类型的情况,要求结合交叉分析表和相应统计图进行分析。
2.分析不同学级的学生选择手机类型的情况,要求结合交叉分析表和相应统计图进行分析。
3.分析不同性别学生选择运营商的情况,要求结合交叉分析表和相应统计图进行分析。
4.分析不同学级的学生选择运营商的情况,要求结合交叉分析表和相应统计图进行分析。
求和项:
手机类型
q4
手机类型
q4
性别
q1
1
2
3
4
5
总计
1
22
66
156
240
10
494
2
11
92
213
236
15
567
总计
33
158
369
476
25
1061
[1]由题可知,男生选择智能机的比较多,而女生选择高端机的比较多。
求和项:
手机类型
q4
手机类型
q4
学级
1
2
3
4
5
总计
1
3
10
3
44
5
65
2
3
16
54
80
153
3
10
52
102
88
5
257
4
6
40
63
88
5
202
5
3
14
114
68
10
209
6
6
18
21
60
105
7
1
8
12
48
69
8
1
1
总计
33
158
369
476
25
1061
[2]专的孩子偏爱智能机
大一孩子偏爱智能机
大二孩子偏爱高端机
大三孩子偏爱智能机
大四孩子偏爱高端机
研一孩子偏爱智能机
研二孩子偏爱智能机
博士生只有一人使用低端机
求和项:
运营商
q5
运营商
q5
性别
q1
1
2
3
4
总计
1
135
66
4
205
2
150
76
6
232
总计
285
142
6
4
437
[3]男生偏爱中国移动
女生偏爱中国移动
求和项:
运营商
q5
运营商
q5
学级
1
2
3
4
总计
1
16
10
26
2
35
28
63
3
76
32
3
111
4
54
32
86
5
48
34
3
4
89
6
35
4
39
7
20
2
22
8
1
1
总计
285
142
6
4
437
[4]专到博都是选择中国移动的人最多,其次是中国联通,选择电信和网通的用户较少
多元线性回归练习题
1.一家电气销售公司的管理人员认为,每月的销售额是广告费用的函数,并想通过广告费用对月销售额作出估计。
近8个月的销售额与广告费用数据见book7.1表。
(1)用电视广告费用作自变量,月销售额作因变量,建立估计的回归方程。
(2)用电视广告费用和报纸广告费用作自变量,月销售额作因变量,建立估计的回归方程。
检验回归方程的线性关系是否显著(=0.05);检验各回归系数是否显著(=0.05)。
SUMMARYOUTPUT
回归统计
MultipleR
0.958663444
RSquare
0.9190356
AdjustedRSquare
0.88664984
标准误差
0.642587303
观测值
8
方差分析
df
SS
MS
F
SignificanceF
回归分析
2
23.43540779
11.7177039
28.37776839
0.001865242
残差
5
2.064592208
0.412918442
总计
7
25.5
Coefficients
标准误差
tStat
P-value
Lower95%
Upper95%
Intercept
83.23009169
1.573868952
52.88247894
4.57175E-08
79.18433275
87.27585063
电视广告费用/万元
2.290183621
0.304064556
7.531899313
0.000653232
1.508560797
3.071806445
报纸广告费用/万元
1.300989098
0.320701597
4.056696662
0.009760798
0.476599399
2.125378798
SUMMARYOUTPUT
回归统计
MultipleR
0.807807408
RSquare
0.652552809
AdjustedRSquare
0.594644943
标准误差
1.215175116
观测值
8
方差分析
df
SS
MS
F
SignificanceF
回归分析
1
16.64009662
16.64009662
11.26881134
0.015288079
残差
6
8.859903382
1.476650564
总计
7
25.5
Coefficients
标准误差
tStat
P-value
Lower95%
Upper95%
Intercept
88.63768116
1.582367131
56.01587609
2.174E-09
84.76576828
92.50959404
电视广告费用/万元
1.603864734
0.47778079
3.356905024
0.015288079
0.434777259
2.772952209
[1]回归方程为:
y=1.60x+88.64
[2]回归方程:
y=2.29x1+1.30x2+83.23
F值0.001865小于0.05,回归方程的线性关系显著
对于x1的系数:
p值0.00065小于0.05,显著
对于x2的系数:
p值0.009761小于0.05,显著
2.一家房地产评估公司想对某城市的房地产销售价格y1与地产的评估价值x1、房产的评估价值x2和使用面积x3建立一个模型,以便对销售价格作出合理预测。
为此,收集了20栋住宅的房地产评估数据见book7.2表。
(1)写出估计的多元回归方程。
(2)检验回归方程的线性关系是否显著(=0.05)。
(3)检验各回归系数是否显著(=0.05)。
SUMMARYOUTPUT
回归统计
MultipleR
0.947362461
RSquare
0.897495632
AdjustedRSquare
0.878276063
标准误差
791.6823283
观测值
20
方差分析
df
SS
MS
F
SignificanceF
回归分析
3
87803505.46
29267835.15
46.69696966
3.87913E-08
残差
16
10028174.54
626760.909
总计
19
97831680
Coefficients
标准误差
tStat
P-value
Lower95%
Intercept
148.700454
574.421324
0.25887001
0.799036421
-1069.018347
0.814738183
0.511988507
1.591321236
0.13109905
-0.270628958
0.820979542
0.211176502
3.887646272
0.001307361
0.373305358
0.135041012
0.065863312
2.050322204
0.057088036
-0.004582972
回归方程:
y=0.81x1+0.82x2+0.135x3+148.7
对于回归方程:
F值远远小于0.05,所以回归方程式显著
对于x1:
0.13大于0.05,不显著
对于x2:
0.001小于0.05,显著
对于x3:
0.057大于0.05,不显著
所以回归方程为:
y+=0.82x2+148.7
3.某农场通过试验取得早稻收获量与春季降雨量和春季温度的数据见book7.3表。
(1)试确定早稻收获量对春季降雨量和春季温度的二元线性回归方程。
解释回归系数的实际意义。
(2)检验回归方程的线性关系是否显著(=0.05)。
(3)检验各回归系数是否显著(=0.05)。
SUMMARYOUTPUT
回归统计
MultipleR
0.995651103
RSquare
0.991321119
AdjustedRSquare
0.986981679
标准误差
261.4310342
观测值
7
方差分析
df
SS
MS
F
SignificanceF
回归分析
2
31226615.26
15613307.63
228.4444623
7.5323E-05
残差
4
273384.7425
68346.18563
总计
6
31500000
Coefficients
标准误差
tStat
P-value
Lower95%
上限95.0%
Intercept
-0.590996232
505.0042289
-0.00117028
0.99912229
-1402.707516
1401.525523
x1
22.38646129
9.600543531
2.331791031
0.080094808
-4.268920799
49.04184339
x2
327.6717128
98.79792462
3.31658498
0.029472413
53.36469864
601.978727
回归方程为:
y=22.39x1+327.67x2-0.59
对于回归方程:
F值远远小于0.05,所以回归方程显著
对于回归系数x1:
0.08大于0.05,不显著
对于回归系数x2:
0.029小于0.05,显著
方差分析练习题
1.从3个总体中各抽取容量不同的样本数据,得到的数据见book5.1表。
检验3个总体的均值之间是否有显著差异?
(=0.01)
方差分析:
单因素方差分析
SUMMARY
组
观测数
求和
平均
方差
列1
5
790
158
61.5
列2
4
600
150
36.66666667
列3
3
507
169
121
方差分析
差异源
SS
df
MS
F
P-value
Fcrit
组间
618.9166667
2
309.4583333
4.657399666
0.040877239
4.256494729
组内
598
9
66.44444444