高中数学抛物线及其性质知识点大全.doc

高中数学抛物线及其性质知识点大全.doc

《高中数学抛物线及其性质知识点大全.doc》由会员分享，可在线阅读，更多相关《高中数学抛物线及其性质知识点大全.doc（9页珍藏版）》请在冰豆网上搜索。

抛物线及其性质

1．抛物线定义：

平面内到一定点F和一条定直线的距离相等的点的轨迹称为抛物线．

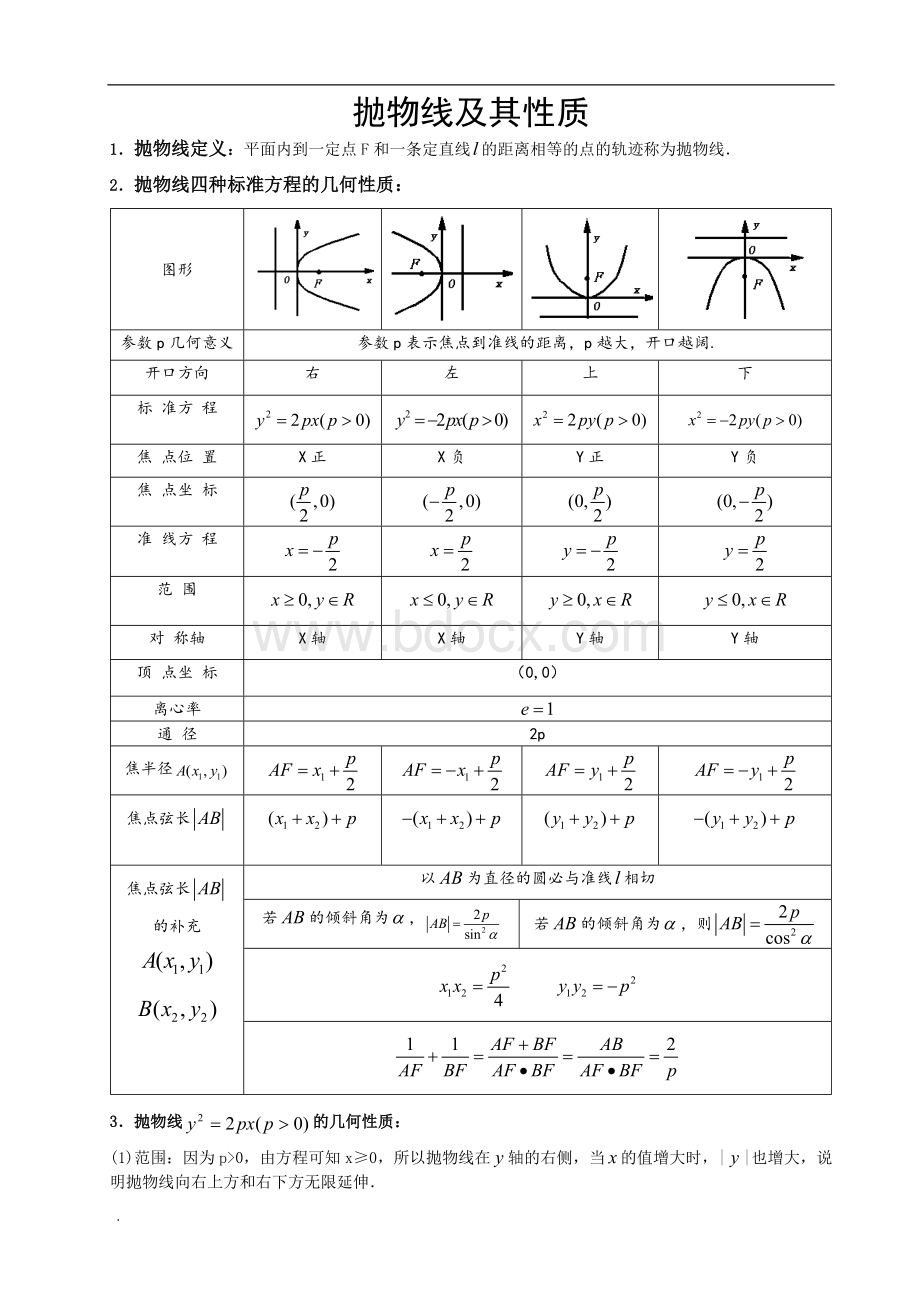
2．抛物线四种标准方程的几何性质：

图形

参数p几何意义

参数p表示焦点到准线的距离，p越大，开口越阔.

开口方向

右

左

上

下

标准方程

焦点位置

X正

X负

Y正

Y负

焦点坐标

准线方程

范围

对称轴

X轴

X轴

Y轴

Y轴

顶点坐标

（0,0）

离心率

通径

2p

焦半径

焦点弦长

焦点弦长的补充

以为直径的圆必与准线相切

若的倾斜角为，

若的倾斜角为，则

3．抛物线的几何性质：

（1）范围：

因为p>0，由方程可知x≥0，所以抛物线在轴的右侧，当的值增大时，||也增大，说明抛物线向右上方和右下方无限延伸．

（2）对称性：

对称轴要看一次项，符号决定开口方向．

（3）顶点（0，0），离心率：

，焦点，准线，焦准距p．

（4）焦点弦：

抛物线的焦点弦，,,则．

弦长|AB|=x1+x2+p,当x1=x2时，通径最短为2p。

4．焦点弦的相关性质：

焦点弦，,，焦点

（1）若AB是抛物线的焦点弦（过焦点的弦），且，，则：

，。

（2）若AB是抛物线的焦点弦，且直线AB的倾斜角为α，则（α≠0）。

（3）已知直线AB是过抛物线焦点F,

（4）焦点弦中通径最短长为2p。

通径：

过焦点垂直于焦点所在的轴的焦点弦叫做通径．

（5）两个相切：

以抛物线焦点弦为直径的圆与准线相切.过抛物线焦点弦的两端点向准线作垂线，以两垂足为直径端点的圆与焦点弦相切。

5．弦长公式：

是抛物线上两点，则

6.直线与抛物线的位置关系

　　直线，抛物线，

　　，消y得：

（1）当k=0时，直线与抛物线的对称轴平行，有一个交点；

（2）当k≠0时，

Δ＞0，直线与抛物线相交，两个不同交点；

Δ=0，直线与抛物线相切，一个切点；

Δ＜0，直线与抛物线相离，无公共点。

（3）若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?

（不一定）

7.关于直线与抛物线的位置关系问题常用处理方法

直线：

抛物线，

①　联立方程法：

设交点坐标为,，则有,以及，还可进一步求出，

在涉及弦长，中点，对称，面积等问题时，常用此法，比如

a.相交弦AB的弦长

或

b.中点,，

②　点差法：

设交点坐标为，，代入抛物线方程，得

将两式相减，可得

a.在涉及斜率问题时，

b.在涉及中点轨迹问题时，设线段的中点为，，

即，

同理，对于抛物线，若直线与抛物线相交于两点，点是弦的中点，则有

（注意能用这个公式的条件：

1）直线与抛物线有两个不同的交点，2）直线的斜率存在，且不等于零）

【经典例题】

（1）抛物线——二次曲线的和谐线

椭圆与双曲线都有两种定义方法，可抛物线只有一种：

到一个定点和一条定直线的距离相等的所有点的集合.其离心率e=1，这使它既与椭圆、双曲线相依相伴，又鼎立在圆锥曲线之中.由于这个美好的1，既使它享尽和谐之美，又生出多少华丽的篇章.

【例1】P为抛物线上任一点，F为焦点，则以PF为直径的圆与y轴（）

相交相切相离位置由P确定

【解析】如图，抛物线的焦点为，准线是

.作PH⊥于H，交y轴于Q，那么，

且.作MN⊥y轴于N则MN是梯形PQOF的

中位线，.故以

PF为直径的圆与y轴相切，选B.

【评注】相似的问题对于椭圆和双曲线来说，其结论则

分别是相离或相交的.

（2）焦点弦——常考常新的亮点弦

有关抛物线的试题，许多都与它的焦点弦有关.理解并掌握这个焦点弦的性质，对破解这些试题是大有帮助的.

【例2】过抛物线的焦点F作直线交抛物线于两点，求证：

（1）

（2）

【证明】

（1）如图设抛物线的准线为，作

，

.两式相加即得：

（2）当AB⊥x轴时，有

成立；

当AB与x轴不垂直时，设焦点弦AB的方程为：

.代入抛物线方程：

.化简得：

∵方程

（1）之二根为x1，x2，∴.

.

故不论弦AB与x轴是否垂直，恒有成立.

（3）切线——抛物线与函数有缘

有关抛物线的许多试题，又与它的切线有关.理解并掌握抛物线的切线方程，是解题者不可或缺的基本功.

【例3】证明：

过抛物线上一点M（x0，y0）的切线方程是：

y0y=p（x+x0）

【证明】对方程两边取导数：

.由点斜式方程：

y0y=p（x+x0）

（4）定点与定值——抛物线埋在深处的宝藏

抛物线中存在许多不不易发现，却容易为人疏忽的定点和定值.掌握它们，在解题中常会有意想不到的收获.

例如：

1.一动圆的圆心在抛物线上，且动圆恒与直线相切，则此动圆必过定点（）

显然.本题是例1的翻版，该圆必过抛物线的焦点，选B.

2.抛物线的通径长为2p；

3.设抛物线过焦点的弦两端分别为，那么：

以下再举一例

【例4】设抛物线的焦点弦AB在其准线上的射影是A1B1，证明：

以A1B1为直径的圆必过一定点

【分析】假定这条焦点弦就是抛物线的通径，那么A1B1=AB=2p，而A1B1与AB的距离为p，可知该圆必过抛物线的焦点.由此我们猜想：

一切这样的圆都过抛物线的焦点.以下我们对AB的一般情形给于证明.

【证明】如图设焦点两端分别为，

那么：

设抛物线的准线交x轴于C，那么

.

这就说明：

以A1B1为直径的圆必过该抛物线的焦点.

●通法特法妙法

（1）解析法——为对称问题解困排难

解析几何是用代数的方法去研究几何，所以它能解决纯几何方法不易解决的几何问题（如对称问题等）.

【例5】（10.四川文科卷.10题）已知抛物线

y=-x2+3上存在关于直线x+y=0对称的相异两点

A、B，则|AB|等于（）

A.3B.4C.3D.4

【分析】直线AB必与直线x+y=0垂直，且线段

AB的中点必在直线x+y=0上，因得解法如下.

【解析】∵点A、B关于直线x+y=0对称，∴设直线AB的方程为：

.由

设方程

（1）之两根为x1，x2，则.

设AB的中点为M（x0，y0），则.代入x+y=0：

y0=.故有.

从而.直线AB的方程为：

.方程

（1）成为：

.解得：

，从而，故得：

A（-2，-1），B（1，2）.，选C.

（2）几何法——为解析法添彩扬威

虽然解析法使几何学得到长足的发展，但伴之而来的却是难以避免的繁杂计算，这又使得许多考生对解析几何习题望而生畏.针对这种现状，人们研究出多种使计算量大幅度减少的优秀方法，其中最有成效的就是几何法.

【例6】（11.全国1卷.11题）抛物线的焦点为，准线为，经过且斜率为的直线与抛物线在轴上方的部分相交于点，，垂足为，则的面积（）

A． B． C． D．

【解析】如图直线AF的斜率为时∠AFX=60°.

△AFK为正三角形.设准线交x轴于M，则

且∠KFM=60°，∴.选C.

【评注】

（1）平面几何知识：

边长为a的正三角形的

面积用公式计算.

（2）本题如果用解析法，需先列方程组求点A的坐标，，再计算正三角形的边长和面积.虽不是很难，但决没有如上的几何法简单.

（3）定义法——追本求真的简单一着

许多解析几何习题咋看起来很难.但如果返朴归真，用最原始的定义去做，反而特别简单.

【例7】（07.湖北卷.7题）双曲线

的左准线为，左焦点和右焦点分别为和；抛物线的线为，焦点为与的一个交点为，则等于（）

A． B． C． D．

【分析】这道题如果用解析法去做，计算会特别繁杂，而平面几何知识又一时用不上，那么就从最原始的定义方面去寻找出路吧.

如图，我们先做必要的准备工作：

设双曲线的半

焦距c，离心率为e，作，令

.∵点M在抛物线上，

，

这就是说：

的实质是离心率e.

其次，与离心率e有什么关系？

注意到：

.

这样，最后的答案就自然浮出水面了：

由于.∴选A..

（4）三角法——本身也是一种解析

三角学蕴藏着丰富的解题资源.利用三角手段，可以比较容易地将异名异角的三角函数转化为同名同角的三角函数，然后根据各种三角关系实施“九九归一”——达到解题目的.

因此，在解析几何解题中，恰当地引入三角资源，常可以摆脱困境，简化计算.

【例8】（09.重庆文科.21题）如图，倾斜角为a的直线经过抛物线的焦点F，且与抛物线交于A、B两点。

（Ⅰ）求抛物线的焦点F的坐标及准线l的方程；

（Ⅱ）若a为锐角，作线段AB的垂直平分线m交

x轴于点P，证明|FP|-|FP|cos2a为定值，并求此定值。

【解析】（Ⅰ）焦点F（2，0），准线.

（Ⅱ）直线AB：

代入

（1），整理得：

设方程

（2）之二根为y1，y2，则.

设AB中点为

AB的垂直平分线方程是：

.

令y=0，则

故

于是|FP|-|FP|cos2a=，故为定值.

（5）消去法——合理减负的常用方法.

避免解析几何中的繁杂运算，是革新、创新的永恒课题.其中最值得推荐的优秀方法之一便是设而不求，它类似兵法上所说的“不战而屈人之兵”.

【例9】是否存在同时满足下列两条件的直线：

（1）与抛物线有两个不同的交点A和B；

（2）线段AB被直线：

x+5y-5=0垂直平分.若不存在，说明理由，若存在，求出直线的方程.

【解析】假定在抛物线上存在这样的两点

∵线段AB被直线：

x+5y-5=0垂直平分，且

.

设线段AB的中点为.代入x+5y-5=0得x=1.于是：

AB中点为.故存在符合题设条件的直线，其方程为：

（6）探索法——奔向数学方法的高深层次

有一些解析几何习题，初看起来好似“树高荫深，叫樵夫难以下手”.这时就得冷静分析，探索规律，不断地猜想——证明——再猜想——再证明.终于发现“无限风光在险峰”.

【例10】（10.安徽卷.14题）如图，抛物线y=-x2+1与x轴的正半轴交于点A，将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线，与抛物线的交点依次为Q1，Q2，…，Qn-1，从而得到n-1个直角三角形△Q1OP1,△Q2P1P2,…,△Qn-1Pn-1Pn-1,当n→∞时，这些三角形的面积之和的极限为.

【解析】∵

设OA上第k个分点为

第k个三角形的面积为：

.

故这些三角形的面积之和的极限

.