苏科版七年级上《第五章走进图形世界》单元测试含答案Word格式文档下载.docx
《苏科版七年级上《第五章走进图形世界》单元测试含答案Word格式文档下载.docx》由会员分享,可在线阅读,更多相关《苏科版七年级上《第五章走进图形世界》单元测试含答案Word格式文档下载.docx(13页珍藏版)》请在冰豆网上搜索。
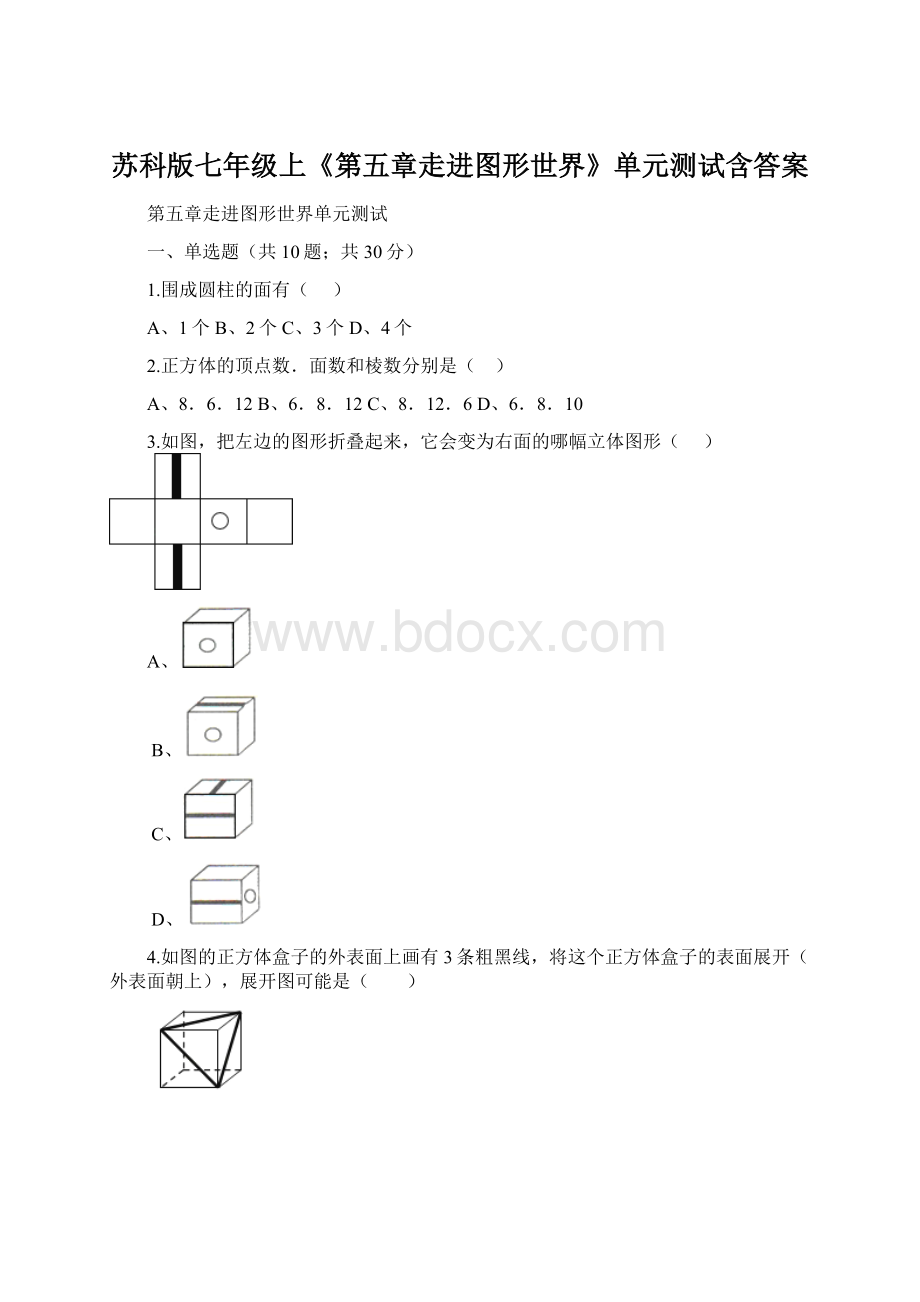
A.六边形B.七边形
C.八边形
D.九边形
7.下列水平放置的几何体中,俯视图是矩形的是( )
A.圆柱
B.长方体
C.三棱柱
D.圆锥
8.用一个平面截去正方体的一个角,则截面不可能是( )
A.等腰直角三角形B.等腰三角形C.锐角三角形D.等边三角形
9.下图中甲和乙周长相比,结果是( )
A.面积一样大B.B的周长较长C.周长一样长D.A的周长较长
10.在同一个圆中,四条半径将圆分割成扇形A,B,C,D的面积之比为2:
3:
4,则最大扇形的圆心角为( )
A.80°
B.100°
C.120°
D.150°
二、填空题(共8题;
共33分)
11.如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是________.
12.笔尖在纸上快速滑动写出了一个又一个字,这说明了________;
车轮旋转时,看起来像一个整体的圆面,这说明了________;
直角三角形绕它的直角边旋转一周形成了一圆锥体,这说明了________.
13.将下列几何体分类,柱体有:
________
,锥体有________
.
14.六棱柱有________
面.
15.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是
________.
16.如图是正方体的一种展开图,其中每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是
17.如图,扇形AOB的面积,占圆O面积的15%,则扇形AOB的圆心角的度数是
18.用一个平面去截长方体,截面________是平行四边形(填“可能”或“不可能”).
三、解答题(共6题;
共36分)
19.一个正方体的表面展开图如图所示,已知这个正方体的每一个面上都填有一个数字
,且各相对面上所填的数字互为倒数,请写出x、y、z的值.
20.一个几何体的三个视图如图所示(单位:
cm).
(1)写出这个几何体的名称
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
21.图中的立体图形是由哪个平面图形旋转后得到?
请用线连起来.
22.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:
cm)
1
2
2+1.5
3
2+3
4
2+4.5
…
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
23.将如图中几何体的截面用阴影部分表示出来,并分别指出它们的形状.
24.如图是半径为2的圆.
(1)在其中画两个不重叠的扇形AOB和扇形BOC,使扇形AOB的圆心角为120°
,扇形BOC的圆心角为90°
;
(2)求第三个扇形AOC的面积.
答案解析
一、单选题
1、【答案】C
【考点】认识立体图形
【解析】【分析】本题考查几何体的面的组成情况,根据圆柱的概念和特征即可得到结果.
圆柱是由上下两个底面,中间一个侧面共3个面组成,故选C.
思路拓展:
解答本题的关键是注意面有平面和曲面之分.
2、【答案】A
【考点】几何体的展开图
【解析】【解答】正方体的顶点数是8个,有6个面,棱有12条.【分析】对棱柱的顶点数与面数的关系有全面的认识并熟记欧拉公式.
3、【答案】B
【解析】【解答】圆面的相邻面是长方形,长方形不指向圆,【分析】根据相邻面、对面的关系,可得答案.
4、【答案】D
【解析】【解答】根据正方体的表面展开图,两条黑线在一列,故A错误,且两条相邻成直角,故B错误,中间相隔一个正方形,故C错误,只有D选项符合条件,
故选D
【分析】根据正方体的表面展开图进行分析解答即可.
5、【答案】D
【考点】点、线、面、体
【解析】【解答】解:
由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选D.
【分析】根据面动成体的原理以及空间想象力即可解.
6、【答案】A
【考点】截一个几何体
正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.
故选A.
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.
7、【答案】B
【考点】简单组合体的三视图
A、圆柱的俯视图为圆,故本选项错误;
B、长方体的俯视图为矩形,故本选项正确;
C、三棱柱的俯视图为三角形,故本选项错误;
D、圆锥的俯视图为圆,故本选项错误.
故选B.
【分析】俯视图是从物体的上面看得到的视图,仔细观察各个简单几何体,便可得出选项.
8、【答案】A
截面经过正方体的3个面时,得到三角形,但任意两条线段不可能垂直,所以截面不可能是等腰直角三角形.
故选:
A.
【分析】让截面经过正方体的三个面,判断其具体形状即可.
9、【答案】C
【考点】认识平面图形
观察图形可知A、B面积无法比较,A、B周长一样长.
故选C.
【分析】根据长方形的性质和周长的定义可知A、B周长一样长.
10、【答案】C
由扇形的面积越大,扇形的圆心角越大,得
D的圆心角最大.
按比例分配,得
D的圆心角为360°
×
42+3+3+4=120°
,
C.
【分析】根据扇形的面积越大,扇形的圆心角越大,可得答案.
二、填空题
11、【答案】的
【解析】【解答】正方体的表面展开图,相对的面之间一定相隔一个正方形,“伟”与“国”是相对面,“大”与“中”是相对面,“的”与“梦”是相对面.
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形.
12、【答案】点动成线;
线动成面;
面动成体
【解析】【解答】本题是点、线、面、体间的动态关系在实际生活中理解.【分析】理论联系实际,深刻的理解点、线、面、体的概念,给出合理的解释.
13、【答案】
(1)
(2)(3);
(5)(6)
【解析】
【解答】柱体分为圆柱和棱柱,所以柱体有:
锥体包括圆柱与圆锥,所以锥体有(5)(6),球属于单独的一类.
故答案为柱体有
(1)
(2)(3);
锥体有(5)(6).
【分析】解这类题首先要明确柱体,椎体的概念和定义,然后根据图示进行解答.
14、【答案】8
六棱柱上下两个底面,侧面是6个长方形,所以共有8个面.
故答案为:
8.
【分析】根据六棱柱的概念和定义即解.
15、【答案】4
【考点】由三视图判断几何体
由主视图可得有2列,根据左视图和俯视图可得每列的方块数如图,
则搭成这个几何体的小正方体的个数是2+1+1=4个.
4.
【分析】根据主视图以及左视图可得出该小正方形共有两行搭成,俯视图可确定几何体中小正方形的列数,从而得出答案.
16、【答案】4
这是一个正方体的平面展开图,共有六个面,其中面“2”与面“4”相对,面“3”与面“5”相对,“1”与面“6”相对.
【分析】利用正方体及其表面展开图的特点解题.
17、【答案】54°
由题意,得
∠AOB360πr2=15%πr2.
解得∠AOB=54°
54°
.
【分析】根据扇形的面积,可得答案.
18、【答案】可能
当截面不垂直于长方体,又经过长方体的4个面时,得到截面为四边形,对边平行且相等,为平行四边形.
【分析】让截面不垂直于长方体,又经过长方体的4个面,动手操作可得到答案.
三、解答题
19、【答案】解:
正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴1与z相对,2与x相对,y与3相对,
∵相对表面上所填的数互为倒数,
∴x=12,y=13,z=1.
【解析】【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
20、【答案】解:
(1)根据三视图可得这个几何体是长方体;
(2)由三视图知,几何体是一个长方体,
长方体的底面是边长为3的正方形,高是4,
则这个几何体的表面积是2×
(3×
3+3×
4+3×
4)=66(cm2).
答:
这个几何体的表面积是66cm2.
故答案为长方体.
【解析】【分析】
(1)由2个视图是长方形,那么这个几何体为棱柱,另一个视图是正方形,那么可得该几何体是长方体;
(2)由三视图知,长方体的底面是边长为3的正方形,高是4,根据长方体表面积公式列式计算即可.
21、【答案】解:
如图.
【解析】【分析】三角形旋转可得圆锥,长方形旋转得圆柱,半圆旋转得球,结合这些规律直接连线即可.
22、【答案】解:
由题意得:
(1)2+1.5(x﹣1)=1.5x+0.5
(2)由三视图可知共有12个碟子
∴叠成一摞的高度=1.5×
12+0.5=18.5(cm)
【解析】【分析】由表中给出的碟子个数与碟子高度的规律,可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1).
23、【答案】解:
如图所示:
如图①所示,截面是一个三角形;
如图②所示,截面是一个梯形.
【解析】【分析】观察图形即可得出答案.
24、【答案】解:
(1)如图所示:
(2)∵∠AOB=120°
,∠BOC=90°
∴∠AOC=150°
故S扇形AOC=150×
π×
22360=53π.
(1)根据扇形定义及题目要求画出即可;
(2)根据扇形的面积公式S=nπr2360计算即可.