线性代数齐次方程组解法Word文档下载推荐.docx
《线性代数齐次方程组解法Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《线性代数齐次方程组解法Word文档下载推荐.docx(14页珍藏版)》请在冰豆网上搜索。
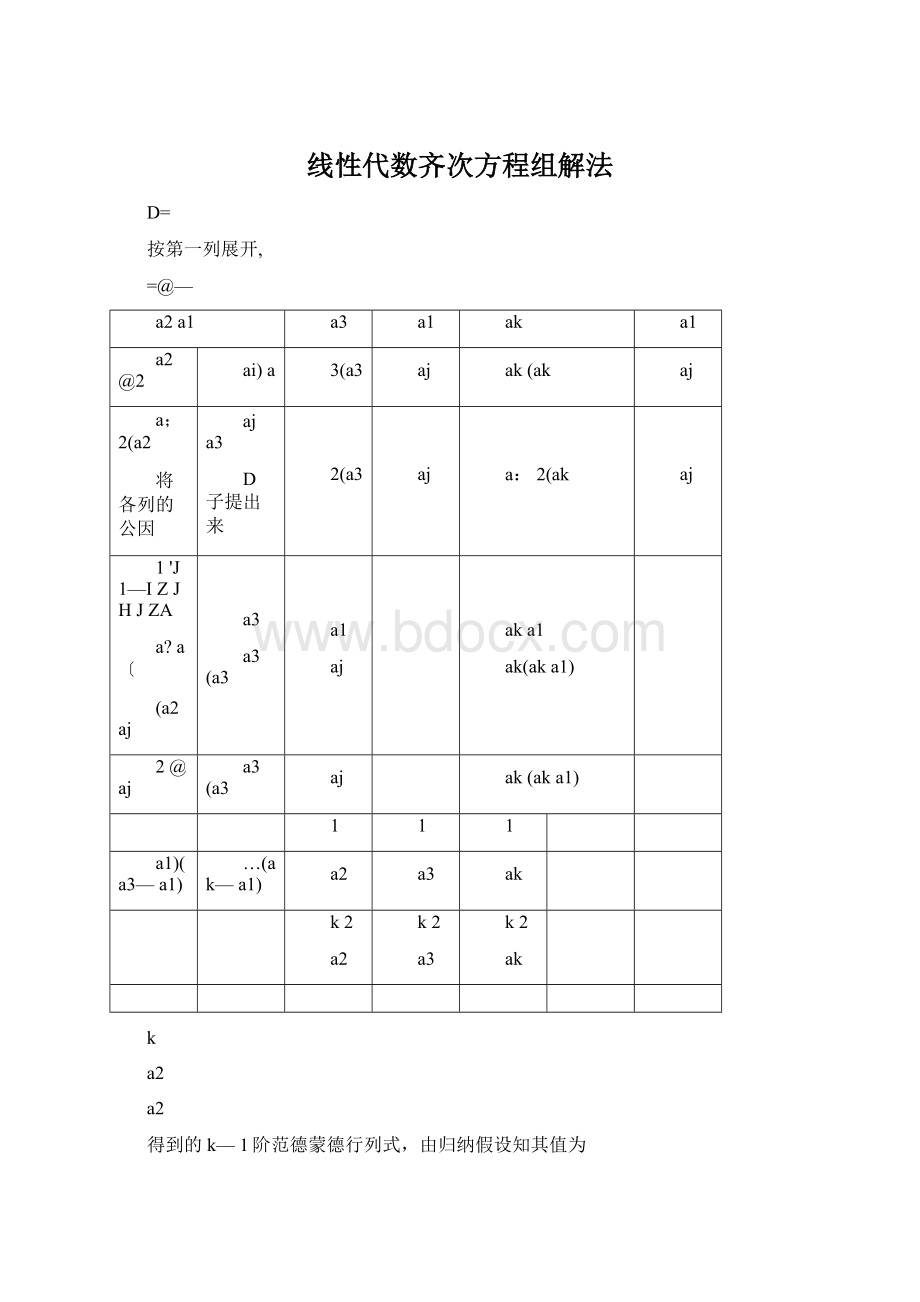
…(ak—a1)
a2
k2
k
得到的k—1阶范德蒙德行列式,由归纳假设知其值为
佝aj)
2jik
是D=(a2—a"
(a3—a1)…(ak—a1)(aiaj)=
j
因此,对于任意正整数n>
2,范德蒙德行列式的展开式都成立。
(aiaj)
证毕
例1.14计算n阶三对角行列式
210
121
012
Dn=
00
21
12
解由行列式的性质1.4,将Dn的第一列的每个元看成两个元之和,得
2
+
Dn=
第二个行列式从第一行开始依次加到下一行,
得
第一个行列式按第一列展开;
Dn=Dn-1+
得到
=Dn-什1
反复利用上面的递推公式,
Dn=Dn-1+1=Dn-2+2==D1+n—仁2+n—仁n+1
例1.15计算n阶行列式
b
(ai丰b,i=1,2,…,n)
an
解对于这个行列式,
采用一种“加边”的技巧。
a1b
a2b
anb
第二列乘以一—
加到第一列上去,第二列乘以
加到第一列上去,依次
类推,最后一列乘以
1加到第一列上去,
ai
i1ai
(ai
1in
b)
1.4
行列式的应用
1.4.1克拉默法则
本小节以行列式为工具,研究解线性方程组的问题。
设n个未知量n个方
程的线性方程组为
它的系数构成的行列式
称为方程组(1.18)的系数行列式。
则该方程组有唯一
(1.21)
定理1.7如果方程组(1.19)的系数行列式不为零,
解:
X1=D1,x2=2...,xn=H
DDD
这里Dj(j=1,2,…,n)是把方程组的常数项b1,b2,…,bn依次替换系数行列式中的第j
列元所得到的n阶行列式。
通常称这个定理为克拉默(G.Cramer)法则。
证明取正整数1,2,…,n中任意一个为j,以如屈,…,Anj分别乘以方程组中第一,第二,…,第n个方程,然后相加,得
nnnn
(ak1Akj)X1+(ak2Akj)X2+…+(akjAkj)Xj+…+(aknAkj)Xn
k1k1k1k1
n
(1.22)
bk1Akj
k1
由性质1.13可知,方程左边Xj的系数为D,而其它的Xi的系数为零;
方程右边恰好是用b1,b2,…,bn依次替换D中第j列每个元所得到的行列式Dj,因此有
Dxj=Dj
令j=i,2,…,n,就得到方程组
Dxi=Dl,DX2=D2,…,Dxn=Dn(1.23)
显然方程组(1.18)的解是(1.23)的解,而当D丰0时,方程组(1.23)有惟一解:
D1D2Dn…八
X1=,X2=,…,Xn=(1.24)
D
因此,方程组(1.18)最多有
一组解。
将(1.24)代入(1.18)
的第i
个方程,得
nDj1n
aij^=^aij(
bkAkj)=—
bk
aijAq=bi(i=1,2,…,n)
j1DDj1k
则(1.24)的解是(1.18)的解。
而且是唯一解。
例1.16解线性方程组
X1
3x2
7X32
2x-|
4x2
3x31
3x-|
7x2
2x33
解系数行列式
3
7
D=
4
=196
由于系数行列式不为零,所以可以使用克拉默法则,方程组有唯一解。
此时
D1=
=—54D2=
=38
D3=
=80
则有
D15427
D2
3819D3
8020
x1
X2
X3
D19698
19698D
19649
用克拉默法则解一个有
n个未知量、
n个方程的线性方程组,
需要计算n+1
个n阶行列式,这样的计算量通常是相当大的,但克拉默法则在理论上具有重要意乂。
1.4.2拉普拉斯定理
行列式按任意一行(列)展开的方法可以推广到按若干行(列)展开。
行列式按若干行(列)的展开式称为拉普拉斯展开式。
在n阶行列式D中任选k行和k列,位于这些行、列交叉处的元按原来顺序排成一个k阶行列式M,称为行列式D的k阶子式;
而划去这k行k列后,剩余的元按原来的顺序排列成的n—k阶行列式N,称为M的余子式;
如果k
阶子式在D中所在的行、列的序号依次为,
i1,i2
,…,ik,j1,j2,…,jk,则把
(1)i1
i2
ikj1
j2j
kN
称为M的代数余子式。
例如
a11
a12
a13
a14
a21
a22
a23
a24
a31
a32
a33
a34
a41
a42
a43
a44
从中取第二、三行,第一、三列,交叉处元组成一个二阶子式,记为M;
M的
余子式记为N,具体写出来就是:
M=
N=
M的代数余子式为(一1)2+3+1+3N=—N
定理1.8在n阶行列式中任取k行(列),则由这k行(列)的元所组成的所有的k阶子式与它的代数余子式的乘积之和,等于行列式的值。
通常把这个定理称为拉普拉斯(Laplace)定理,证明从略。
例1.17利用拉普拉斯定理将下面的行列式按第一、二两行展开
1100
1210
0131
0014
解D中由第一、二两行的元组成的二阶子式共有六个
11
M1=
=3,M2=
=1,M3=
=0
10
=1,M5=
=0,M6=
20
M4=
其中M1,M2,M4的代数余子式为
由拉普拉斯定理知
D=M1A1+M2A2+M3A3+M4A4+M5A5+M6A6=3X13+1X4=43
a0
0a
拉普拉斯定理计算行列式的值比较简单。
例1.18计算n阶行列式
0b
—2次相邻列的互换,使最后一列换到第二列的位置上
a
D=(—1)n—2
=
用拉普拉斯定理,可得
=an_2(a2—b2)
143方阵与行列式
行列式作为方阵的一个数字特征,具有如下性质(其中A,B为n阶方阵,
为数)
性质
1.14
detAT=detA
1.15
det(A)=ndet(A)
证明
设
a1n
a21
a22
a2n
A=
an1
an2
ann
则
a11
a12
a〔n
a1n
a2n
及det(
A)=
an2
an1
an2
ann
依据行列式的性质,将
det(A)中每一行中的公因子提出,得到
a1n
det(A)=n
=ndet(A)
性质1.16设A、B为n阶方阵,则有
det(AB)=(detA)•(detB)(此性质称为行列式的乘法定理)(1.25)
证明设C=AB,并设A=(aij)n>
n,B=(bij)nXn,C=(Cij)n>
<
构造2n阶行列式如下:
根据拉普拉斯定理,
把
D按照前
b11
b12
bm
b21
b22
b2n
bn1
bn2
bnn
n行展开,有D=(detA)(detB)
另一方面,对D中的后n列实施行列式的性质
1.11,将第k列(1<
kwn)
乘以bkj加入到第n+j列中去,使得原来矩阵
B位置上的每个元都变为零,
C11
C12
C21
C22
an1an2
annCn1Cn2
000
c1n
C2n
Cnn
其中Gj=a,kbkj,即C=(Gj)=AB
i1
冉用拉晋拉斯疋理
,把
D按照最后
n行展开,有
D=(-1)s
(detC)=(—1)s(-1)n(detC)
其中s=[(n+1)+(n+2)+…+2n]+(1+2+…+n)=n(2n+1),s+n=n(2n+2)为偶数。
所以D=detC=det(AB)故det(AB)=(detA)(detB)证毕
显然,行列式的乘法定理可以推广到有限个方阵相乘的情形,即
det(A1A2…Ak)=(detA1)(detA2)…(detAk)
144行列式和伴随矩阵与逆矩阵的关系
前面给出了逆矩阵的概念以及用行初等变换求逆矩阵的方法,禾U用行列式还可给出判明可逆阵的一个简单条件,并给出逆阵的一个公式。
为此,需要引入n阶矩阵A的转置伴随阵的定义。
为A的转置伴随阵(adjugatematrix)或伴随矩阵,用记号A*表示。
定理1.8设A是n阶矩阵,adjA为其转置伴随矩阵,则有
(1.26)
A(adjA)=(adjA)A=(detA)E
证明因为