个人所得税分配方案文档格式.docx
《个人所得税分配方案文档格式.docx》由会员分享,可在线阅读,更多相关《个人所得税分配方案文档格式.docx(20页珍藏版)》请在冰豆网上搜索。
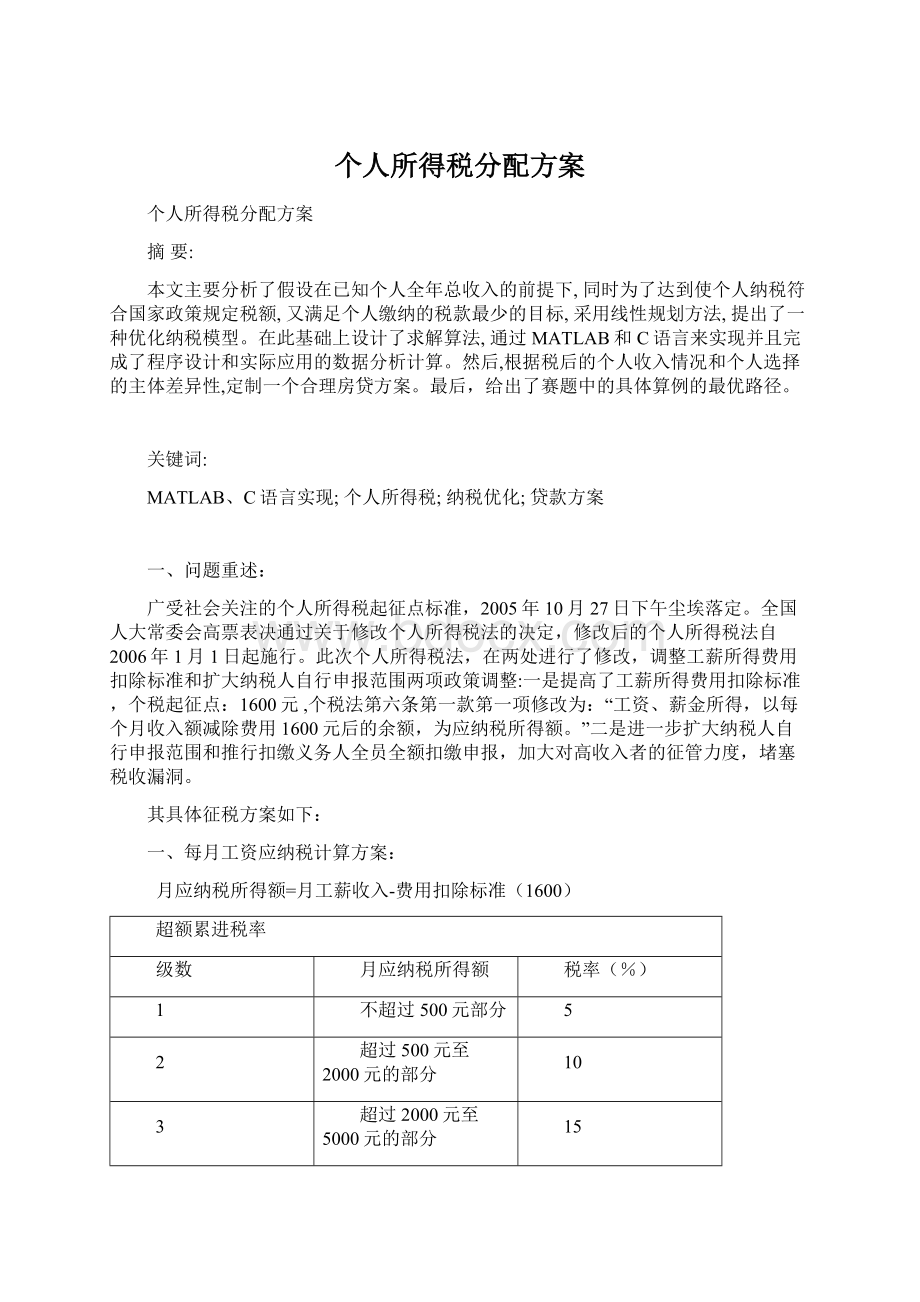
1.
请根据以上新的纳税方案,为某公司职员制定其每年收入分配方案使其年度纳税总额最少(纳税性
(((假设其年收入为10万元,公司允许其自行决定每月收入和年终一次性奖金的分配数额)。
2.
请制定一张该公司职员年度收入最优分配方案表,年收入从3万元以1000元为间隔到15万元。
二、问题分析:
(1)问题一纳税方案必须在纳税义务发生之前依法进行。
纳税人进行纳税筹划时,必须在法律法规允许的范围内,合理预期应税所得,在纳税义务发生前完成筹划工作。
这是合理实施纳税方案的前提。
纳税总额S分为2部分,一部分为月工资部分的所需上交的税额S1,另外一部分为年终奖部分所需上交的税额S2。
要使S最小的就是保证月工资纳税和年终奖纳税总额最少。
通过直观的分析,企业发放年终奖奖金以及员工每月工资的不均衡发放,必然导致个人所得税税负提高,实际到手的收人减少。
每月均匀发放工资薪金会降低个人所得税的税率,会减少应纳个人所得税金额。
企业在发放年终一次性奖金时.应抓住税率临界点。
本方案即在寻找这个税率的临界点。
(2)问题二是建立在问题一的基础上所作的进一步推广。
求出年收入从3万元以1000元为间隔到15万元各种情况所对应的最优工资、奖金分配方案使所交税收最少。
三、模型假设
(1)、为便于计算,问题中所涉及的下述方案中不含个人所得实物收人、福利费中列支等应税收人,仅指工资薪金中的应税收人,没考虑可以税前扣除的基本养老保险金、住房公积金和住房补贴,实际操作时应作为纳税筹划因。
个人的年总收入仅分为:
每月的月收入和年终奖的收入。
(2)、员工已知其年收入,并且公司允许其自行决定每月收入和年终一次性奖金的分配数额。
(3)为便于计算,每个月的工资金额按100元为间隔递增来比较相应的税收。
四、符号说明
S
为员工一年的总共需要上交的税收
S1
为员工月收入中需上交的税收
S2
员工年终奖收入中需上交的税收
Z
员工年总收入
G
员工月工资收入
N
员工年终奖收入
N0
员工年终奖收入分摊到每个月
xi+1600
第i个月的工资
y
表示年末奖金的1/12
fxi
第i个月应付个人所得税
fy
表示1/12*年终奖金应付个人所得税
M
年收入
五、模型建立与求解
问题一:
模型的建立与求解
(1)、根据中华人民共和国个人所得税纳税标准,某月所得工资G,工资部分每月所需上交的税收为S1。
S1与G之间的关系式如下所示。
(2)员工年终奖收入N(年终一次性奖金纳税计算与每月收入纳税计算独立进
行),年终一次性奖金纳税计算方案:
先将雇员当月内取得的全年一次性奖金,
除以12个月即N0,按其商数确定适用税率和速算扣除数。
然后,将雇员个人当
月内取得的全年一次性奖金,按所确定的适用税率计算征税。
针对个人的全年纳税,建立如下模型:
S=S1×
12+S2×
12
其中的约束条件:
Z=G×
12+N;
(G,N>
0)
在进行模型求解之前,我们首先要提出一个已被证明的论点,即:
假设没
有年终奖,在税前年收入为定值Z元时,这时的Z=G×
12;
将Z平均分配到12
个月,即G。
如果每月的工资可按员工意愿,则存在g1,g2,g3……g12。
当g1=
g2=g3=……=g12时,所需上交的税额为最小。
本模型是基于每个月收入为一
个定值且每月都相等。
问题一模型的求解。
由于在该问题中,个人收入的总额不变,且纳税的方式不变。
而由于各个月
的地位都相同,即不管先后,如果两个月的收入额相交换不影响总体交纳个人所
得锐额。
由多元微积分学中的无条件极值,我们可以容易地证明出,只有当每个
月的收入相等,即任意的gi为同一值时,纳税最少。
因此我们建立如下模型
Minz=12*fx+12*fy
根据以上的公式可以通过群举法的方法,以年终奖间隔100元开始从1递增
到100000,可以得到以下的结果:
总税收与年终奖和年终奖金的关系
每月工资与该月工资对应的税收
年终奖与年终奖对应的税收
在年终奖为56800元左右时,相应的税和最小。
然后在通过56700~56900之间的群举,可以得到以下的最终结果。
最佳情况总的税收值9120.0元
最佳情况总的月工资额3600.3元
最佳情况工资部分的月税收值175.0375元
最佳情况的年终奖56797元
最佳情况年终奖的税收值7019.5元
问题二模型的建立与求解:
本题的模型是建立在问题一的基础上,列出了年收入从3万元以1000元为间隔到15万元的所有情况。
运用MATLAB程序可以得到不同年收入的基本情况,列表与其相对应的图如下
职员年度收入最优分配方案表
最佳月工资
月工资税
年终奖
30000
2000
540
6000
31000
2083.4
590
5999
32000
2108.4
680
6699
33000
2108.9
780
7693
34000
880
8699
35000
2108.7
980
9696
36000
1080
10699
37000
2109.2
1180
11690
38000
1280
12690
39000
2109.4
1380
13687
40000
2434.2
1480
10790
41000
1580
15690
42000
1680
16696
43000
2434
1780
13792
44000
1880
18699
45000
1980
19690
46000
2100
2080
20800
47000
2100.7
2180
21792
48000
2234.2
2280
21190
49000
2380
23800
50000
2166.9
2480
23997
51000
2484.2
2580
52000
2333.3
2680
24000
53000
2416.9
2780
54000
2500.2
2880
23998
55000
2583.5
2980
56000
2666.7
3080
57000
2750.2
3180
58000
2833.3
3280
59000
2916.7
3380
60000
3000.2
3480
61000
3083.3
3580
62000
3166.7
3680
63000
3250.2
3780
64000
3333.4
3880
23999
65000
3416.7
3980
66000
3500.2
4080
67000
3583.3
4180
68000
3600
4320
24800
69000
4470
25800
70000
3609.2
4620
26690
71000
4770
27800
72000
4920
28800
73000
3608.4
5070
29699
74000
4125.1
5220
24499
75000
4100.8
5370
25790
76000
3808.4
5520
30299
77000
4375.1
5670
24499
78000
5820
28790
79000
4058.4
5970
80000
4100.5
6120
30794
81000
4225.1
6270
30299
82000
4100.3
6420
32796
83000
6570
33794
84000
4475.1
6720
85000
4100.1
6870
35799
86000
7020
36794
87000
4725.8
7170
30290
88000
7320
44690
89000
7470
45800
90000
4975.8
7620
91000
7770
47690
92000
7920
48800
93000
8070
49690
94000
3737.9
8220
49145
95000
3600.2
8370
51798
96000
3759.2
8520
50890
97000
3987.9
8670
49145
98000
8820
54798
99000
4009.2
8970
50890
100000
3600.3
9120
56797
101000
4175.1
9270
50899
102000
4404.6
9420
103000
9570
59797
104000
4425.1
9720
105000
4654.6
9870
106000
3834
10020
59992
107000
4675.1
10170
108000
4904.6
10320
109000
4083.5
10470
59998
110000
4925.8
10620
111000
5154.6
10770
59145
112000
4333.5
10920
59998
113000
5175.8
11070
114000
5404.6
11220
115000
4583.5
11370
116000
5425.8
11520
117000
5654.6
11670
118000
4833.5
11820
119000
5675.8
11970
120000
5001
12120
59988
121000
5083.5
12270
122000
5167.3
12420
123000
5251
12570
124000
5333.5
12720
125000
5416.8
12870
59998
126000
5501
13020
127000
5583.5
13170
128000
5666.8
13320
129000
5751
13470
59988
130000
5833.5
13620
131000
5916.8
13770
132000
6000.3
13920
59997
133000
6084
14070
59992
134000
6166.8
14220
135000
6250.3
14370
59997
136000
6334
14520
137000
6416.8
14670
138000
6500.3
14820
139000
6584
14970
140000
6600.1
15200
60799
141000
6600
15450
61800
142000
15700
62800
143000
6700.1
15950
62599
144000
16200
64800
145000
16450
65800
146000
16700
66800
147000
16950
67800
148000
17200
68800
149000
17450
69800
150000
17700
70800
六、模型的评价
优点
(1)线性规划的数学方法年收入分配方案和贷款方案使得个人所得税最少
(2)本文充分考虑了该夫妇符合个人住房公积金贷款和不符合个人住房公积金贷款两种情况,并且对等额本金还款和等额本息还款进行了比较,得出了较合理的还款方式。
缺点:
在问题一中我们只考虑了工资大于1600的情况;
对于问题三我们假设较多且较理想;
程序的编写比较繁琐。
七、改进及推广
模型的改进
该模型在解决还按揭贷款时,只提供了等额本息还款方式的解决模型,而没有讨论等额本金还款方式。
如果要让模型更具普适性,应该提供等额本金还款方式的解决模型。
模型的推广
用理财的思路去考虑最为合理的收入使用分配应该是非常有必要的。
尤其对于那些工作比较稳定,但收入平平的工薪阶层房贷者而言,过多的还款压力很可能使其不堪重负,沦为“房奴”一族。
在本模型中充分考虑了该问题,将月供还贷压力降低到最低,同时考虑也考虑了工薪阶层房贷者的生活压力及生活开支。
八、参考文献
[1]XX百科,住房公积金,,2011/9/3。
[2]XX百科,公积金贷款利率,,2011/9/3。
[3]和讯银行,及时贷款利率查询,,2011/9/3。
[4]张建勋,纪纲,C程序设计实用教程,中国铁道出版社,2009。
[5]姜启源,谢金星,叶俊,数学模型(第三版),高等教育出版社,203-222,2003.8。
[6]周永正,詹棠森,方成鸿,邱望仁,数学建模,同济大学出版社,7-14,205-212,2010.8。
九、附录
具体代码
程序一
%N总收入;
G每月的工资;
J为年收入的奖金;
S为所需上交的税
%N=G*12+J
Sz=100000;
%税收的初始值
fori=0:
100:
J(i+1)=i;
%年收入的奖金
G(i+1)=(100000-J(i+1))/12;
%每月的工资
if(G(i+1)<
=1600)
S1(i+1)=0;
G0=0;
else
G0=G(i+1)-1600;
%月应纳税所得额=月工薪收入-费用扣除标准(1600)
end
if(G0<
=500&
G0>
S1(i+1)=G0*0.05;
elseif(G0>
500&
G0<
=2000)
S1(i+1)=(G0-500)*0.1+25;
2000&
=5000)
S1(i+1)=(G0-2000)*0.15+25+150;
5000&
=20000)
S1(i+1)=(G0-5000)*0.25+25+150+450;
J0=J(i+1)/12;
%奖金纳税平均月收入
S2(i+1)=0;
S2(i+1)=J0*0.05;
if(J0<
J0>
=0)
S2(i+1)=(J0-500)*0.1+25;
elseif(J0>
J0<
S2(i+1)=(J0-2000)*0.15+25+150;
S2(i+1)=(J0-5000)*0.25+25+150+450;
S2(i+1)=S2(i+1)*12;
%该年所上交的奖金税
S(i+1)=S1(i+1)*12+S2(i+1);
if(S(i+1)<
=Sz)
Sz=S(i+1);
Sg=S1(i+1);
Sj=S2(i+1);
I=i;
end
subplot(3,1,1)
plot(S,G*12,'
b+'
S,J,'
r+'
)
legend('
年总税收与月工资'
'
年税收与年终奖'
title('
总税收与年工资和年终奖金'
subplot(3,1,2)
plot(G,S1,'
*'
每月工资与该月工资对应的税收'
subplot(3,1,3)
plot(J,S2,'
年终奖与年终奖对应的税收'
fori=(I-100):
(I+100)
J=i;
G=(100000-J)/12;
if(G<
G0=G-1600;
J0=J/12;
%奖金纳税平均月收入
S2(i+1)=S2(i+1)*12;
S(i+1)=S1(i+1)*12+S2(i+1);
if(S(i+1)<
best_tax=Sz%output('
最佳情况总的税收值'
month_payment=(100000-I)/12%output('
最佳情况总的月工资额'
best_payment_tax=Sg%output('
最佳情况工资部分的月税收值'
reward=I%output('
最佳情况的年终奖'
best_reward_tax=Sj%output('
最佳情况年终奖的税收值'
附录二:
forq=30000:
1000:
%N总收入;
G每月的工资;
J为年收入的奖金;
S为所需上交的税
Sz=150000;
%____________________