中考数学专题突破导练案第四讲几何初步与图形的变化试题文档格式.docx

中考数学专题突破导练案第四讲几何初步与图形的变化试题文档格式.docx

《中考数学专题突破导练案第四讲几何初步与图形的变化试题文档格式.docx》由会员分享，可在线阅读，更多相关《中考数学专题突破导练案第四讲几何初步与图形的变化试题文档格式.docx（11页珍藏版）》请在冰豆网上搜索。

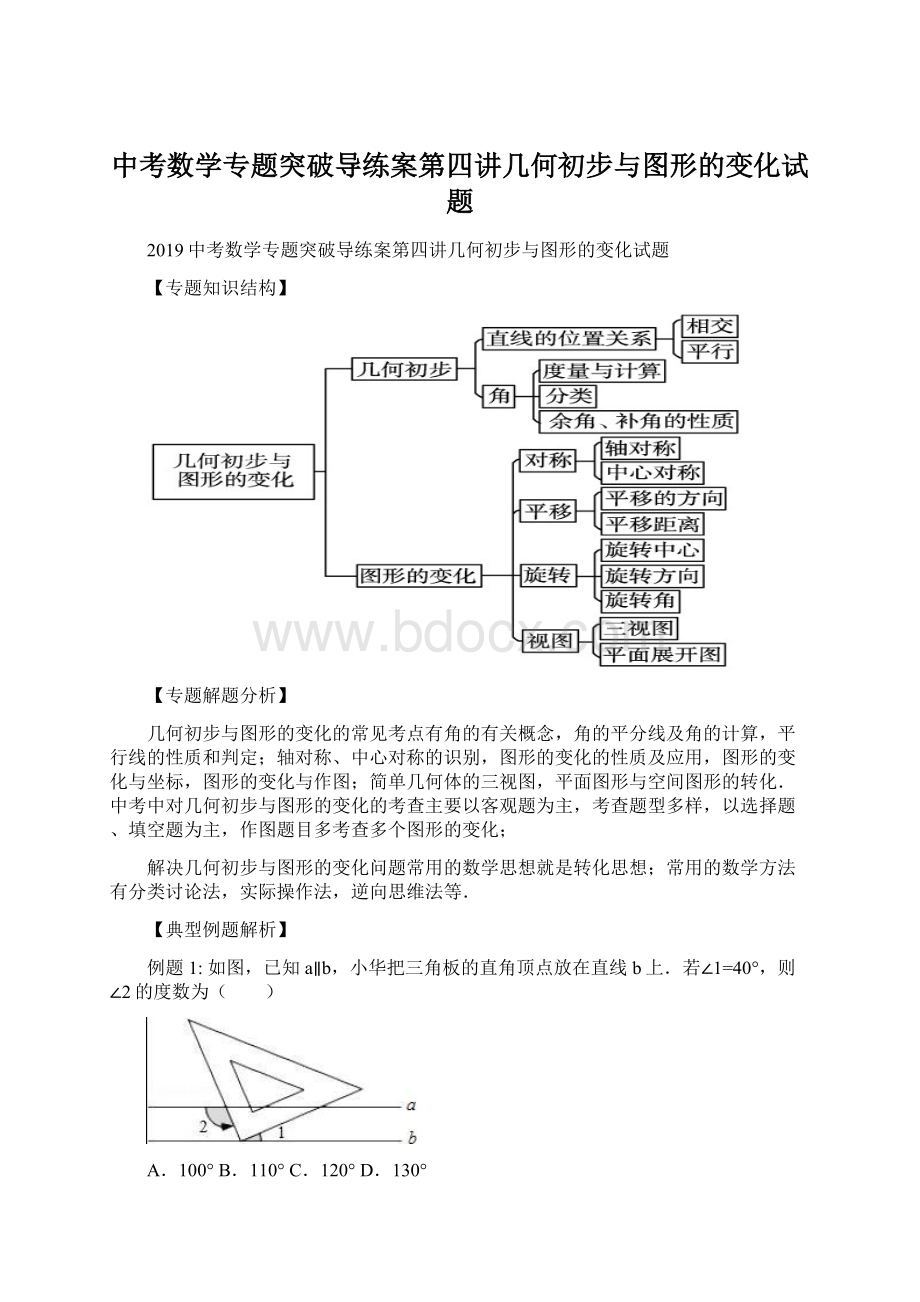
∵∠1+∠3=90°

，

∴∠3=90°

∵a∥b，

∴∠2+∠3=180°

∴∠2=180°

﹣50°

=130°

故选：

D．

例题2:

（2017四川绵阳）如图所示的几何体的主视图正确的是（　　）

A．

B．

C．

D．

【考点】U2：

简单组合体的三视图．

【分析】先细心观察原立体图形和正方体的位置关系，结合四个选项选出答案．

由图可知，主视图一个矩形和三角形组成．

故选D．

例题3：

（2017山东临沂）如图，将直尺与含30°

角的三角尺摆放在一起，若∠1=20°

，则∠2的度数是（　　）

A．50°

B．60°

C．70°

D．80°

【分析】首先根据三角形外角的性质求出∠BEF的度数，再根据平行线的性质得到∠2的度数．

∵∠BEF是△AEF的外角，∠1=20°

，∠F=30°

∴∠BEF=∠1+∠F=50°

∵AB∥CD，

∴∠2=∠BEF=50°

故选A．

【点评】本题主要考查了平行线的性质，解题的关键是掌握三角形外角的性质，此题难度不大．

例题4：

将一把直尺与一块三角板如图放置，若∠1=45°

，则∠2为（　　）

A．115°

B．120°

C．135°

D．145°

平行线的性质；

IL：

余角和补角．

【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3，再根据两直线平行，同位角相等可得∠2=∠3．

如图，由三角形的外角性质得，∠3=90°

+∠1=90°

+45°

=135°

∵直尺的两边互相平行，

∴∠2=∠3=135°

故选C．

例题5：

如图1是一把园林剪刀，把它抽象为图2，其中OA=OB．若剪刀张开的角为30°

，则∠A=　75　度．

【考点】KH：

等腰三角形的性质．

【分析】根据等腰三角形的性质和三角形的内角和即可得到结论．

∵OA=OB，∠AOB=30°

∴∠A=

=75°

故答案为：

75．

例题6：

（2017.湖南怀化）如图，直线a∥b，∠1=50°

A．130°

B．50°

C．40°

D．150°

【分析】利用平行线的性质得出∠1=∠3=50°

，再利用对顶角的定义得出即可．

如图：

∵直线a∥直线b，∠1=50°

∴∠1=∠3=50°

∴∠2=∠3=50°

B．

【达标检测评估】

一、选择题：

1.（2017湖北襄阳）如图，BD∥AC，BE平分∠ABD，交AC于点E．若∠A=50°

，则∠1的度数为（　　）

A．65°

C．55°

D．50°

【分析】根据平行线的性质，得到∠ABD=130°

，再根据BE平分∠ABD，即可得到∠1的度数．

∵BD∥AC，∠A=50°

∴∠ABD=130°

又∵BE平分∠ABD，

∴∠1=

∠ABD=65°

2.（2017.江苏宿迁）如图，直线a，b被直线c，d所截，若∠1=80°

，∠2=100°

，∠3=85°

，则∠4度数是（　　）

A．80°

B．85°

C．95°

D．100°

【考点】JB：

平行线的判定与性质．

【分析】先根据题意得出a∥b，再由平行线的性质即可得出结论．

∵∠1=80°

∴∠1+∠2=180°

∴a∥b．

∵∠3=85°

∴∠4=∠3=85°

故选B．

3.（2016·

广西百色·

3分）下列关系式正确的是（　　）

A．35.5°

=35°

5′B．35.5°

50′C．35.5°

＜35°

5′D．35.5°

＞35°

5′

【考点】度分秒的换算．

【分析】根据大单位化小单位乘以进率，可得答案．

A、35.5°

30′，35°

30′＞35°

5′，故A错误；

B、35.5°

30′＜35°

50′，故B错误；

C、35.5°

5′，故C错误；

D、35.5°

5′，故D正确；

4.如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么下列结论错误的是（　　）

A．∠BAO与∠CAO相等B．∠BAC与∠ABD互补

C．∠BAO与∠ABO互余D．∠ABO与∠DBO不等

【分析】根据平行线的想着角平分线的定义即可得到结论．

∵AC∥BD，

∴∠CAB+∠ABD=180°

∵AO、BO分别是∠BAC、∠ABD的平分线，

∴∠BAO与∠CAO相等，∠ABO与∠DBO相等，

∴∠BAO与∠ABO互余，

5.（2017山东东营）已知a∥b，一块含30°

角的直角三角板如图所示放置，∠2=45°

，则∠1等于（　　）

B．135°

C．155°

D．165°

【分析】先过P作PQ∥a，则PQ∥b，根据平行线的性质即可得到∠3的度数，再根据对顶角相等即可得出结论．

如图，过P作PQ∥a，

∴PQ∥b，

∴∠BPQ=∠2=45°

∵∠APB=60°

∴∠APQ=15°

∴∠3=180°

﹣∠APQ=165°

∴∠1=165°

【点评】本题主要考查了平行线的性质，解题时注意：

两直线平行，内错角相等，同旁内角互补．

二、填空题：

6.（2017年湖南郴州）如图，直线EF分别交AB、CD于点E，F，且AB∥CD，若∠1=60°

，则∠2=　120°

　．

【分析】两直线平行，同位角相等，据此可得到∠EFD，然后根据邻补角概念即可求出∠2．

∴∠DFE=∠1=60°

﹣∠DFE=120°

120°

两直线平行，同位角相等．

7.．（2017山东威海）如图，直线l1∥l2，∠1=20°

，则∠2+∠3=　200°

【分析】过∠2的顶点作l2的平行线l，则l∥l1∥l2，由平行线的性质得出∠4=∠1=20°

，∠BAC+∠3=180°

，即可得出∠2+∠3=200°

过∠2的顶点作l2的平行线l，如图所示：

则l∥l1∥l2，

∴∠4=∠1=20°

+20°

=200°

；

200°

【点评】本题考查了平行线性质：

两直线平行，同位角相等；

两直线平行，同旁内角互补；

两直线平行，内错角相等．

8.（2016·

四川宜宾）如图，直线a∥b，∠1=45°

，∠2=30°

，则∠P=　75　°

【考点】平行线的性质．

【分析】过P作PM∥直线a，求出直线a∥b∥PM，根据平行线的性质得出∠EPM=∠2=30°

，∠FPM=∠1=45°

，即可求出答案．

过P作PM∥直线a，

∵直线a∥b，

∴直线a∥b∥PM，

∵∠1=45°

∴∠EPM=∠2=30°

∴∠EPF=∠EPM+∠FPM=30°

9.（2016·

浙江省湖州市·

4分）如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是　90　度．

【分析】如图2，AB∥CD，∠AEC=90°

，作EF∥AB，根据平行线的传递性得到EF∥CD，则根据平行线的性质得∠1=∠AEF，∠2=∠CEF，所以∠1+∠2=∠AEC=90°

如图2，AB∥CD，∠AEC=90°

作EF∥AB，则EF∥CD，

所以∠1=∠AEF，∠2=∠CEF，

所以∠1+∠2=∠AEF+∠CEF=∠AEC=90°

故答案为90．

三、解答题：

10.如图，Rt△ABC中，∠ACB=90°

，将Rt△ABC向下翻折，使点A与点C重合，折痕为DE．求证：

DE∥BC．

【考点】翻折变换（折叠问题）；

解二元一次方程组．

【分析】

（1）根据方程组的解法解答即可；

（2）由翻折可知∠AED=∠CED=90°

，再利用平行线的判定证明即可．

（2）∵将Rt△ABC向下翻折，使点A与点C重合，折痕为DE．

∴∠AED=∠CED=90°

∴∠AED=∠ACB=90°

∴DE∥BC．

11.如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是多少？

A．8B．6C．4D．2

【考点】角平分线的性质．

【分析】过点P作PE⊥BC于E，根据角平分线上的点到角的两边的距离相等可得PA=PE，PD=PE，那么PE=PA=PD，又AD=8，进而求出PE=4．

过点P作PE⊥BC于E，

∵AB∥CD，PA⊥AB，

∴PD⊥CD，

∵BP和CP分别平分∠ABC和∠DCB，

∴PA=PE，PD=PE，

∴PE=PA=PD，

∵PA+PD=AD=8，

∴PA=PD=4，

∴PE=4．