全国高考理科数学历年真题圆锥曲线Word格式.docx

全国高考理科数学历年真题圆锥曲线Word格式.docx

《全国高考理科数学历年真题圆锥曲线Word格式.docx》由会员分享，可在线阅读，更多相关《全国高考理科数学历年真题圆锥曲线Word格式.docx（26页珍藏版）》请在冰豆网上搜索。

的方程是

y2

A．4

C．2

D．2

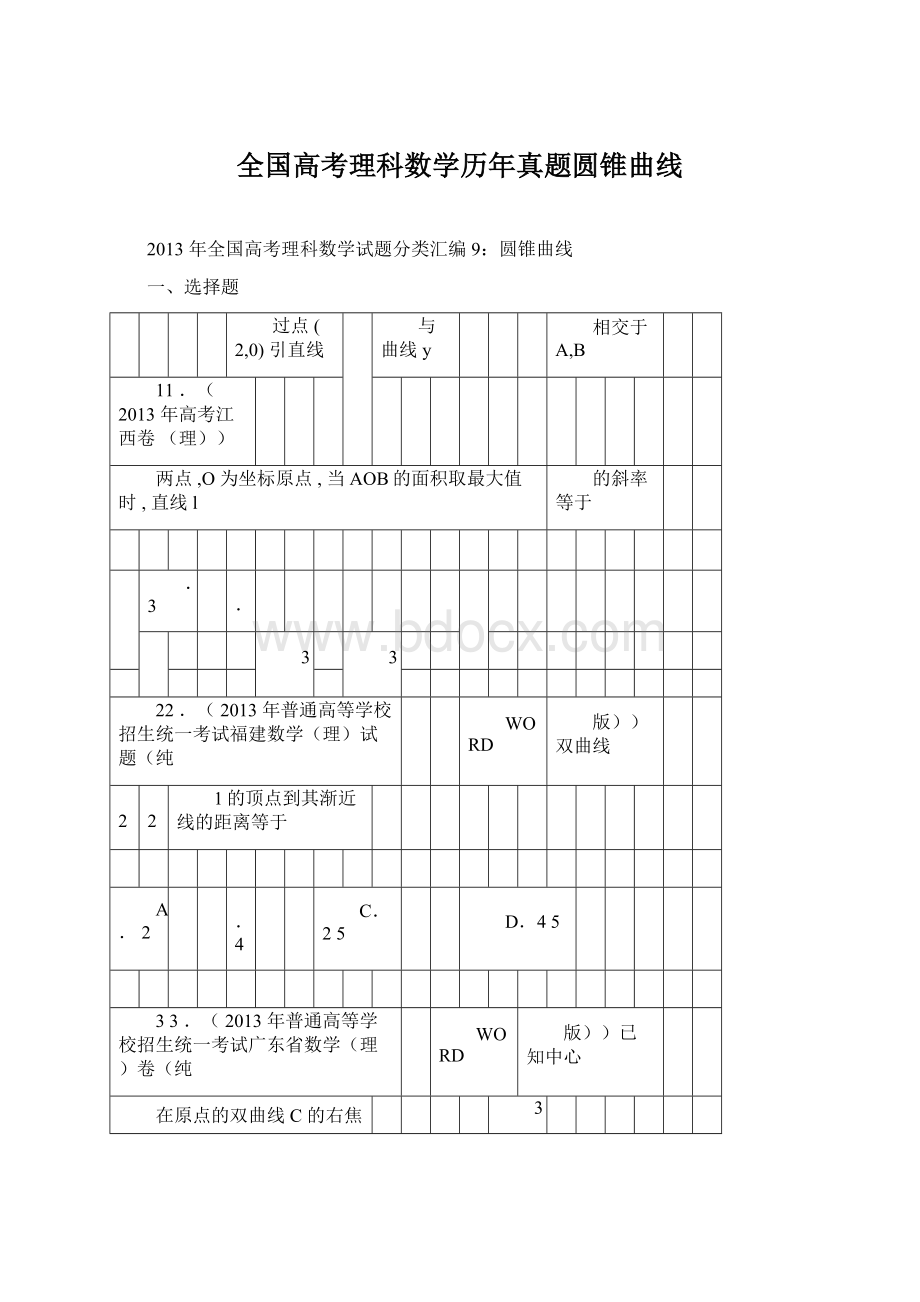
已知双曲线C:

a

0,b0

的离心

44．（2013年高考新课标

1（理））

a2

b2

率为5,则C的渐近线方程为

A．y

1x

B．y

C．y

D．y

55．（2013年高考湖北卷（理））已知0

则双曲线

C1

:

1与

sin

cos

C2

1的

sin2

tan2

1/14

A．实轴长相等

B．虚轴长相等C．焦距相等

D．离心率相

66．（2013

年高考四川卷（理））抛物线y2

4x的焦点到双曲线x2y2

的渐

近线的距离是

A．1

B．3

C．1

D．3

77．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯

WORD版））如图,F1,F2

是椭圆C1:

x2

1与双曲线C2的公共焦点,

A,B分别是C1,

C2在第

二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是

y

O

F2

F1

B

（第9题图）

．2

D．6

88．（2013

年普通高等学校招生统一考试天津数学（理）试题（含答案）

）已知双曲线

1（a

0,b

0）

的两条渐近线与抛物线y2

2px（p0）的准线分别

交于A,B两点,

O为坐标原点.若双曲线的离心率为2,

△AOB

的面积为3,

则p=

A．1

C．2

D．3

99．（2013年普通高等学校招生统一考试大纲版数学

（理）WORD

版含答案（已校对））椭圆

C:

1的左、右顶点分别为

A1,A2,点P在C上且直线PA2的斜

率的取值范围是

2,1,那么直线PA1斜率的取值范围是

2/14

A．

C．

D．

，

8

1010．（2013

年普通高等学校招生统一考试大纲版数学（理）

版含答案（已校对））已

知抛物线C:

y2

8x与点M

2,2

过C的焦点且斜率为k的直线与

C交于A,B两点,若MAMB

0,则k

B．2

1111．（2013

年高考北京卷（理））若双曲线x2

1的离心率为

3,则其渐近

线方程为

A．y=±

2x

B．y=

2x

1212．（2013

年普通高等学校招生统一考试山东数学（理）试题（含答案）

）已知抛物线

（p

C1:

2p

0）的焦点与双曲线C2:

3

的右焦点的连线

交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐

近线,则p

A．16

B．8

C．3

1（理））已知椭圆

b0）的右焦点为

1313．（2013

年高考新课标

E:

b

F（3,0）

过点F的直线交椭圆于A,B两点.若AB的中点坐标为（1,1）,

则E的方程为

A．x2

B．x2

C．x2

D．x2

45

36

27

18

9

1414．（2013

年普通高等学校招生统一考试新课标

Ⅱ卷数学（理）（纯WORD

版含答案））设

3/14

抛物线C:

2px（p0）的焦点为F,点M在C上,MF

5,若以MF

为直径的圆过点（0,2）,

则C的方程为

A．y2

4x或y2

8x

B．y2

2x或y2

C．y2

4x或y2

16x

D．y2

1515．（2013年上海市春季高考数学试卷（含答案））已知A、B为平面内两定点,过该

平面内动点M作直线AB的垂线,垂足为N.若

ANNB,其

MN

中为常数,

则动点M的轨迹不可能是

A．圆

B．椭圆

C．抛物线

D．双曲线

1616．（2013

年普通高等学校招生统一考试重庆数学（理）试题（含答案）

）已知圆

x2

y3

圆C2:

x

M,N分别是圆C1,C2

1,

上的动点,P为x轴上的动点,

则PM

PN的最小值为

A．524

B．171

C．622

D．17

二、填空题

1717．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）

（已校对纯

WORD版含附

加题））双曲线x2

1的两条渐近线的方程为_____________.

16

抛物线x

2py（p

的焦点为F,其准线与双

1818．（2013年高考江西卷（理））

曲线x2

1相交于A,B两点,

若

ABF

为等边三角形,则

P_____________

1919．（2013年高考湖南卷（理））设F1,F2

是双曲线C:

0,b0）的两

个焦点,P是C上一点,若PF1

PF2

6a,且PF1F2的最小内角为30,

则C的离心率为___.

4/14

2020（．

设AB是椭圆

的长轴,点C在上,且CBA,

2013年高考上海卷（理））

若AB=4,BC2,则的两个焦点之间的距离为________

2121

．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯

WORD版））已知直线

ya交抛物线yx2于A,B两点.若该抛物线上存在点

C,使得

ABC为直角,则a的取值范围为________.

2222

．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）

加题））抛物线yx2在x1处的切线与两坐标轴围成三角形区域为

D（包含三角形内部与边界）.若点P（x,y）是区域D内的任意一点,

则x2y的取值范围是__________.

2323．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附

加题））在平面直角坐标系xOy中,椭圆C的标准方程为

1（a0,b

0）,右焦点为F,右准线为l,短轴的一个端点为

B,设原点到直线BF的距离为d1,

F到l的距离为d2,若d2

6d1,则

椭圆C的离心率为_______.

2424．（2013

年普通高等学校招生统一考试福建数学（理）试题（纯

版））椭圆

0）的左.右焦点分别为F1,F2

焦距为2c,若直线

21（ab

3（x

c）与椭圆

的一个交点M满足MF1F2

2MF2F1,则该椭圆

的离心率等于__________

2525.（2013

年高考陕西卷（理））双曲线x2

1的离心率为5,则m等于

m

______.

2626．（2013

年普通高等学校招生统一考试辽宁数学（理）试题（

WORD版））已知椭圆

5/14

y21（ab0）的左焦点为F,C与过原点的直线相交于

A,B

两点,

连接AF,BF,若AB

10,AF6,cos

4,则C的离心率

e=______.

2727．（2013

年上海市春季高考数学试卷

（含答案））抛物线y2

8x的准线方程是

_______________

2828．（2013

年普通高等学校招生全国统一招生考试江苏卷（数学）

（已校对纯WORD

版含附

在平面直角坐标系

xOy

中,设定点

A（a,a）

P是函数y

x0

加题））

图象上一动点,若点P，A之间的最短距离为22,则满足条件的实

数a的所有值为_______.

2929．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯

WORD版））设F为抛

物线C:

4x的焦点,过点P（1,0）的直线l交抛物线C于两点A,B,

点Q为线段AB的中点,若|FQ|2,则直线的斜率等于________.

三、解答题

130．（2013年上海市春季高考数学试卷

（含答案））本题共有2

个小题,第1小题满

分4分,第2小题满分9

分.

已知椭圆C的两个焦点分别为F1（1，0）、F2（1，0）,短轴的两个端点

分别为B1、B2

（1）若F1B1B2为等边三角形,求椭圆C的方程;

（2）若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P、Q

两点,且F1PFQ1

求直线l的方程.

已知椭圆C:

1,（ab0）的两个焦点分

231．（2013年高考四川卷（理））

别为F1（1,0）,F2（1,0）

且椭圆C经过点P（4,1）.

6/14

（Ⅰ）求椭圆C的离心率;

（Ⅱ）设过点A（0,2）的直线l与椭圆C交于M、N两点,点Q是线段

上的点,且

求点

Q

的轨迹方程.

|AQ|2

|AM|2

|AN|2

332．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））椭圆

3,过F1

21（ab0）的左、右焦点分别是F1,F2,离心率为

且垂直于x轴的直线被椭圆C截得的线段长为1.

（Ⅰ）求椭圆C的方程;

（Ⅱ）点P是椭圆C上除长轴端点外的任一点,

连接PF1,PF2,设

F1PF2

的角平分线PM交C的长轴于点M（m,0）

求m的取值范

围;

（Ⅲ）在（Ⅱ）的条件下,过P点作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k0,

试证明

11

kk1kk2

为定值,并求出这个定值.

1,

（3分+5分+8分）如图,已知曲线C1:

433．（2013年高考上海卷（理））

曲线C2:

|y||x|1,P是平面上一点,若存在过点P的直线与C1,C2

都

有公共点,则称P为“C1—C2型点”.

（1）在正确证明C1的左焦点是“C1—C2型点”时,要使用一条过该

焦点的直线,试写出一条这样的直线的方程

（不要求验证）;

（2）

设直线y

kx与C2有公共点,求证|k|

1,进而证明原点不是

“C1—C2型点”;

（3）

求证:

圆x

内的点都不是“C—C型点”.

7/14

534．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD版））如图,在正

方形OABC中,O为坐标原点,点A的坐标为（10,0）,点C的坐标为

（0,10）.分别将线段OA和AB十等分,分点分别记为A1,A2,....A9和

B1,B2,....B9,连结OBi,过Ai做x轴的垂线与OBi交于点

Pi（iN*,1i9）.

（1）求证:

点Pi（iN*,1i9）都在同一条抛物线上,并求该抛物线

E的方程;

（2）过点C做直线与抛物线E交于不同的两点M,N,若OCM与

OCN的面积比为4:

1,求直线的方程.

635．（2013年高考湖南卷（理））过抛物线E:

0）的焦点F作斜率分

别为k1,k2的两条不同的直线l1,l2,且k1

k22

l1与E相交于点

A,B,l2与E相交于点C,D.以AB,CD为直径的圆M,圆N（M,N为圆心）

的公共弦所在的直线记为l.

（I）若k10,k20,证明;

FMFN2P2;

（II）若点M到直线l的距离的最小值为75,