概率习题答案文档格式.docx
《概率习题答案文档格式.docx》由会员分享,可在线阅读,更多相关《概率习题答案文档格式.docx(27页珍藏版)》请在冰豆网上搜索。
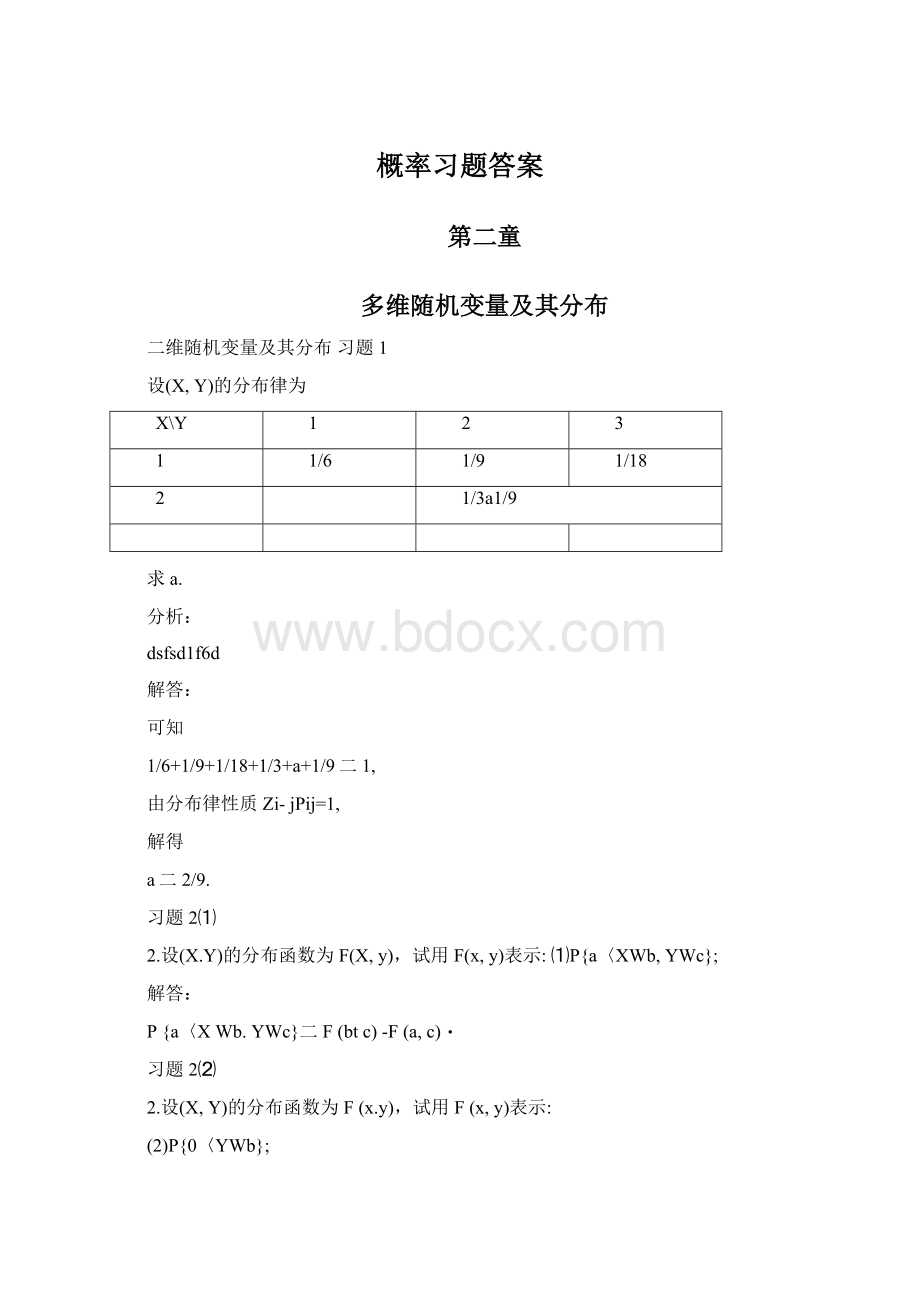
23,0<
4
P{X=1FY=1}+P{X=1,Y=2)+P(X=1,Y=3)
二P(X=1,Y=1}+P{X=1,丫二2}+P{X=1,丫二3}=14+0+0=14.
习题3⑵
3.设二维离散型随机变量的联合分布如下表:
(2)P{1WXW2,3WYW4};
P{1WXW2,3WYW4}
二P(X=1,丫二3}+P(X=1,丫二4}+P{X二2,Y二3}+P{X二2,Y二4}二0+116+0+14二516.
试求:
(3)F(2,3).
F(2,3)二P(1,1)+P(1,2)+P(1,3)+P(2,1)+P(2,2)+P(2,3)=14+0+0+116+14+0=916.
习题4
设X,Y为随机变量,且
P{XMO,YM0}=37,P{XM0}二P{Y20}二47,
求P(max(X,Y}>
0}.
解答:
P{max{X,Y}M0}=P(X,Y至少一个大于等于0)
二P{XMO}+P{Y20}—P{XMO,YM0}
二47+47-37二57.
(X,Y)只取下列数值中的值:
(0,0),(-1,1),(-1,13),(2,0)
且相应概率依次为16,13,112,512,请列出(X,Y)的概率分布表,并写出关于Y的边缘分布.
(1)因为所给的一组概率实数显然均大于零,且有16+13+112+512二1,故所给的一组实数必是某二维随机变量(X,Y)的联合概率分布.因(X,Y)只取上述四组可能值,故事件:
{X二T,Y二0),{X二0,Y二13,
{X二0,Y二1},{X二2,Y二13,{X=2rY=1)
均为不可能事件,其概率必为零.因而得到下表:
01/31
-1
01/121/3
1/600
5/1200
(2)P{Y二0}二P{X=-1,丫二0}+P{X二0,Y二0}+P{X二2,Y二0}
=0+16+512=712,同样可求得
P(Y=13=112,P(Y=1}=13,
关于的Y边缘分布见下表:
Y
pk
7/121/121/3
习题6
设随机向量(X,Y)服从二维正态分布N(0,0.102,102,0),其概率密度为
f(x,y)=1200nex2+y2200,求P{XWY}.
由于P{XWY}+P{X>
Y}=,且由正态分布图形的对称性,知
P{XWY}=P{X>
Y},
故P{XWY}=2.
习题7
设随机变量(X,Y)的概率密度为
f(x,y)二{k(6-x-y),0<
x<
2,2<
y<
40,其它,
(1)确定常数&
(2)求P(X<
1fY<
3};
⑶求P(X<
);
⑷求P{X+YW4}.
如图所示
⑴由J*-00+00J-oo+oof(x,y)dxdy=1,确定常数k.
J*02J*24k(6-x-y)dydx=kJ02(6-2x)dx二8kh,
所以k=18.
(2)P(X<
1rY<
3}=J*01dxJ2318(6-x-y)dy=38.
(3)P{X<
}=fJ2418(6-x-y)dy二2732.
(4)P{X+YW4}二J02dxJ24-x18(6-x-y)dy二23.
习题8
已知X和Y的联合密度为
f(x,y)二{cxy,0WxW1,0WyW10,其它,
试求:
(1)常数c;
(2)X和Y的联合分布函数F(x,y).
(1)由于1=J-oo+ooJ*-oo+oof(x,y)dxdy二cj*01J*01xydxdy=c4,c二4.
⑵当xWO或yWO时,显然F(x,y)二0;
当x>
1,y>
1时,显然F(x,y)=1;
设0有
F(x,y)=f_ooxJ-°
°
yf(urv)dudv二4JOxuduJ*Oyvdv=x2y2.
设0WxW1,y>
1,有
F(x,y)二P{X,YWy}二4JOxuduJ*01ydy二x2.
最后,设x>
1,0WyW1,有
F(x,y)二P{XW1,YWy}二4J01xdxJ*Oyvdv二y2.
函数F(x,y)在平面各区域的表达式
F(x,y)二{0,xWO或
yW0x2,0WxW1,y>
1x2y2,0WxW1,OWyW,x>
习题9
设二维随机变量(X,Y)的概率密度为
f(X,y)二{(2-x),0WxW1,xWyWIO,其它,求边缘概率密度fY(y).
fX(x)=J-oo+oof(x,y)dy
={J(2-x)dy,OWxWIO,其它二{(2-x),OWxGO,其它.
fY(y)=J-oo+oof(x,y)dx
={J(2-x)dx,OWyW10,其它二{(4y-y2),0Wy0,其它.
习题10
设(X,Y)在曲线y二x2,y二X所围成的区域G里服从均匀分布,求联合分布密度和边缘分布密度.
解答=
区域G的面积A二J01(x-x2)dx二16,由题设知(X,Y)的联合分布密度为
f(x,y)={6,0WxW1,x2WyWxO,其它,从而fX(x)=J-oo+oof(x,y)dy=6Jx2xdy=6(x-x2),0WxW1,即
fX(x)=(6(x-x2),OWx0,其它,fY(y)=J*-oo+oof(Xfy)dx=6J*yydx二6(y-y),0WyW1,即fY(y)=(6(y-y),OWy0,其它.
条件分布与随机变■的独立性习题1
二维随机变量(X,Y)的分布律为
01
7/157/307/301/15
(1)求Y的边缘分布律;
(2)求P{Y二0|X二0},P{Y=1|X二0};
(3)判定X与Y是否独立?
(1)由(x,y)的分布律知,y只取0及1两个值.
P{y二0}二P{x二0,y二0}+P{x=1,y=0}二715+730二
P{y=1)=Ei=01P(x=i,y=1}=130+115=
(2)P(y=0|x二0}二P{x二0,y二0}P{x二0}二23,
P(y=1|x二0}二13.
(3)已知P{x二0,y二0}二715,由
(1)知P{y二0}二,类似可得
P(x=0}=
因为P{x=0,y=0}#=P{x=0}・P{y=0},所以x与y不独立.
习题2
将某一医药公司9月份和8份的青霉素针剂的订货单分别记为X与Y.据以往积累的资料知X和Y的联合分布律为
55
010.010.010
求边缘分布律;
(2)求8月份的订单数为51时,9月份订单数的条件分布律.
(1)边缘分布律为
X
对应X的值,将每行的概率相加,可得P{X二i}・
当Y二51时,X的条件分布律为
P{X二k|Y=51}=P{X=kty=51}P(Y=51J=pkFrk=51152,53,54,55.
列表如下:
k
P{X=k|Y二51}
6/287/285/285/285/28
习题3
已知(X,Y)的分布律如下表所示,试求:
(1)在Yh的条件下.X的条件分布律;
(2)在X二2的条件下,Y的条件分布律.
012
1/41/8001/301/601/8
由联合分布律得关于X,Y的两个边缘分布律为
3/81/37/24
5/1211/241/8
故
(1)在Y二1条件下,X的条件分布律为
X|(Y=1)
3/118/110
(2)在X二2的条件下,Y的条件分布律为
Y|(X二2)
4/703/7
已知(X,Y)的概率密度函数为f(x,y)={3x,0<
1,0<
x0,其它,求:
(1)边缘概率密度函数;
(2)条件概率密度函数.
(1)fX(x)=J-oo+oof(x.y)dy二{3x2,0<
10,其它.
fY(y)=J-oo+oof(x,y)dx=(32(1-y2),0<
(2)对VyG(0,1),
fX|Y(x|y)=f(x,y)fY(y)={2x1-y2,y<
1r0,其它,对VxG(0,1),
fYIx(y|x)二f(x,y)fX(x)二{1x,(Ky〈x0・其它.
习题5
X与Y相互独立,其概率分布如表(a)及表(b)所示,求(X,Y)的联合概率分布,p{X+Y=1}rP{X+Y=#0}・
-2-101/2
pi
1/41/31/121/3
表(a)
-1/213
1/21/41/4
表⑹
由X与Y相互独立知
P{X二xi,Y二yi}二P{X二xi]P(Y=yj),
从而(X,Y)的联合概率分布为
-1/2
-2-
P{X=-2JP{Y=-1/2)P(X=-1}P{
P{X=-2JP{Y=1}P{X=-1}
P{X=-2)P{Y=3)P{X=-1}
101
Y=-1/2)P(X=0)P{Y=-1/2)P(X
P{Y=1)P(X=0)P(Y=1)P(
P{Y二3}P{X二0}P(Y=3)P{
/2
二1/2}P{Y二-1/2}
X=1/2)P(Y=1)
X=1/2}P{Y=3}
亦即表
1/81/161/161/61/121/121/241/481/481/61/121/12
P{X+y=1}=P{X二-2,y二3}+P{X=0,Y=1}=116+148=112,P(X+Y=#0)=1-P(X+Y=0}
=1-P{X=-1,Y=1)-P(X=12,Y=-12=1-112-16=34.
某旅客到达火车站的时间X均匀分布在早上7:
55-8:
00,而火车这段时间开出的时间Y的密度函数为
fY(y)=(2(5-y)25,OWyW50,其它,
求此人能及时上火车站的概率.
由题意知X的密度函数为
fX(x)二{15,0WxW50,其它,因为X与Y相互独立,所以X与Y的联合密度为:
fXY(x,y)二{2(5-y)125,0WyW5,0WxW50,其它,故此人能及时上火车的概率为
P(Y>
X)二j05Jx52(5-y)125dydx=13.
设随机变量X与Y都服从N(OJ)分布,且X与Y相互独立,求(X,Y)的联合概率密度函数.
由题意知,随机变量X,Y的概率密度函数分别是
fX(x)=12ne-x22,fY(y)=12ne-y22
因为X与Y相互独立,所以(X,Y)的联合概率密度函数是
f(x,y)=12ne-12(x+y)2.
设随机变量X的概率密度
f(x)=12e-|x|(-oo<
+oo)f
问:
X与|X|是否相互独立?
若X与|X丨相互独立,贝wa>
0,各有
P{XWa,|X|Wa}二P{XWa}•P(|X|Wa},
而事件{|X|Wa}u{XWa},故由上式有
P(IX|Wa}=P{XWa}•P{|X|Wa},
=P{|X|Wa}(—P{XWa})二0
=>
P{|X^a|}=0或1二P{XWa}・(Va>
0)
但当a>
0时,两者均不成立,出现矛盾,故X与|X丨不独立.
设X和Y是两个相互独立的随机变量,X在(0,1)±
服从均匀分布,Y的概率密度为
fY(y)={12e-y2,y>
00,yWO,
(1)求X与Y的联合概率密度;
(2)设有a的二次方程a2+2Xa+Y二0,求它有实根的概率.
(1)由题设易知
fX(x)={1,0<
10,其它,
又X,Y相互独立,故X与Y的联合概率密度为
f(x,y)=fX(x)•fY(y)={12e-y2,0<
1,y>
00,其它;
⑵因{a有实根}二{判别式△2二4X2-4Y$0}二{X22Y},故如图所示得到:
P{a有实根}=P{X2NY}二JSx2>
yf(x,y)dxdy二J*OldxJ0x212e-y2dy=-J01e-x22dx=1-[J*-°
1e-x22dx-J*-°
0e-x22dx]
=1-2n[12nJ-oo1e-x22dx-12nJ*-o°
0e-x22dx]
=1-2n[①
(1)-0(0),
又①⑴二,①(0)二,于是<
D
(1)-<
D(0)=所以
Pfa有实根]=1-2n[<
D(0)]^X=
二维随机变■函数的分布
习题1
设随机变量X和Y相互独立,且都等可能地取1,2,3为值,求随机变量U二max{X,Y}和V二min{X,Y}的联合分布.
由于UNV,可见P{U=iTV=j)=O(i<
j).此外,有
P{U二V二i}二P{X二Y二i}=1/9(i=1,2,3),
P{U=irV=j}=P{X二i,Y二j}+P{X二jtY=i)=2/9(i>
j)r
于是,随机变量U和V的联合概率分布为
v\概率\u
2/9
设(X,Y)的分布律为
-112
-12
1/101/53/101/51/101/10
(1)Z二X+Y;
(2)Z二XY;
(3)Z二X/Y;
(4)Z二max{X,Y}的分布律.
与一维离散型随机变量函数的分布律的计算类型,本质上是利用事件及其概率的运算法则•注意,z的相同值的概率要合并.
概率
(X,Y)X+YXYX/Ymax(x,Y)
(-1,-1)(-1J)(-1,2)(2,-1)(2,1)(2,2)-2011341-1-2-2241-1-1/2-2
于是
(1)
X+Y
-20134
1/101/51/21/101/10
XY
1/21/51/101/101/10
X/Y
-2-1-1/212
1/51/53/101/51/10
max(X,Y)
1/101/57/10
设二维随机向量(X,Y)服从矩形区域D二{(x,y|0WxW2,0WyW1}的均匀分布,且
求U与V的联合概率分布.
依题(U,V)的概率分布为
P{U二0,V二0}二P{XWY,XW2Y}二P{XWY}
二JO1dxJx112dy二14,
P{U二0,V二1}=P{XWY,X>
2Y}=0,
P{U二1,V=0}二P(X>
Y,XW2Y}二P{Y<
XW2Y}
=J*01dyJ*y2y12dx=14,
P{U=1,VP1
=1-P{U二0,V二0}-P{U二0,Vh}-P{U=1,V=0)=1/2,
即
u\v
1/401/41/2
设(X,Y)的联合分布密度为
f(x,y)=12ne-x2+y22,Z二X2+Y2,
求Z的分布密度.
FZ(z)二P{ZWz}二P{X2+Y2Wz).当z<
0时,FZ(z)=P(0)=0;
当zMO时,
FZ(z)二P{X2+Y2Wz2}=J*Jx2+y2Wz2f(x,y)dxdy
=12nJJx2+y2Wz2e-x2+y22dxdy二12ttJ02nd0JOze-p22pdp
二JOze-p22pdp=1-e-z22.
故z的分布函数为
FZ(z)=(1-e-z22,z^OO,z<
0.
Z的分布密度为
fZ(z)=(ze-z22,z>
00,zWO.
设随机变量(X,Y)的概率密度为f(xry)={12(x+y)e-(x+y),x>
0,y>
00,其它,
(1)问X和Y是否相互独立?
(2)求Z二X+Y的概率密度.
(1)fX(x)=J*-oo+oof(x,y)dy
={J0+°
12(x+y)e-(x+y)dy,x>
00,xW0
\under21ine令
x+y二t(J*x+°
12te~tdt=12(x+1)e-x,x>
00,xWO,
由对称性知fY(y)=(12(y+1)e-y,y>
00,yWO,显然
f(x,y)*fX(x)fY(y),x>
0,所以X与Y不独立.
(2)用卷积公式求fZ(z)=J-oo+oof(x,z-x)dx.
当(x>
0z-x>
0即(x>
0x<
z时,f(x,z-x)去0,所以
当zWO时,fZ(z)=0;
当z>
0时,fZ(z)=J0z12xe-xdx=12z2e-z.
于是,Z二X+Y的概率密度为
fZ(z)={12z2e-z,z>
设随机变量X,Y相互独立,若X服从(0,1)上的均匀分布,Y服从参数1的指数分布,求随机变量Z二X+Y的概率密度.
据题意,X,Y的概率密度分布为
fX(x)={1r0<
10,其它,fY(y)=(e-y,y$00,y<
0,由卷积公式得Z二X+Y的概率密度为
fZ(z)=J-oo+oofx(x)fY(z-x)dx二J-oo+oofx(z-y)fY(y)dy
二JO+oofX(z-y)e-ydy.
由0<
z-y<
1得z-1<
z,可见:
当zW0时,有fX(z-y)=0,故fZ(z)=J0+oo0-e-ydy二0;
当z>
0时,
fZ(z)二JO+°
fX(z-y)e-ydy二Jmax(0,z-1)ze-ydy二e-max(0,z-1)-e-
z,
fZ(z)二{0,zW01-e-z,0<
z^1e1-z-e-z,z>
f(x,y)二(be-(x+y),0<
+°
0,其它.
(D试确定常数b;
(2)求边缘概率密度fX(x),fY(y);
(3)求函数U=max{X,Y)的分布函数.
(1)由J-oo+ooJ*-oo+oof(xry)dxdy=1,确定常数b.
J01dxJO+°
be-xe-ydy=b(1-e-1)=1,
f(x,y)=(11-e-1e-(x+y),0<
Or其
它.
(2)由边缘概率密度的定义得
fX(x)二{J0+°
11-e-1e-(x+y)dy=e~x1-e-x,0<
1,0,其它,fY(x)={f0111-e-1e-(x+y)dx=e-yF0<
+8,0,其它
(3)因为f(x,y)=fX(x)fY(y),所以X与Y独立,故
FU(u)=P(max(X,Y)Wu}二P{XWu,YWu}=FX(u)FY(u),其中FX(x)二j0xe-t1-e-1dt=1-e-x1-e-1,0<
1,
所以FX(x)二{0,xWO,1-e-x1-e-1,0<
1,1,x^1.
同理FY(y)二{jOye-tdt=1-e-y,0<
0,yWO,
因此FU(u)二{0,u<
0,(1-e-u)21-e-1,0^u<
1,1-e-ufu^1.
设系统L是由两个相互独立的子系统L1和L2以串联方式联接而成,L1和L2的寿命分别为X与Y,其概率密度分别为
(f>
1(x)={ae-axFx>
00,xWO,(j>
2(y)={Pe-py,y>
00,yWOt其中a>
0,B>
0,a工B,试求系统L的寿命Z的概率密度.
设Z二min{X,Y},则
F(z)二P{ZMz}二P{min(X,Y)Wz}
=1-P{min(X,Y)>
z}=1-P{XMz,YMz}
=1-[1P(X<
z)][1-P{Y<
z}]=1-[1-F1{z}][1-F2{z}]
由于
F1(z)二{jOzae-axdx=1-e-a乙zNOO,z<
0,
F2(z)={1-e-pz,zMOO,z<
故
F(z)=