中考数学试题分类解析汇编专题V压轴题Word格式.docx

中考数学试题分类解析汇编专题V压轴题Word格式.docx

《中考数学试题分类解析汇编专题V压轴题Word格式.docx》由会员分享，可在线阅读，更多相关《中考数学试题分类解析汇编专题V压轴题Word格式.docx（15页珍藏版）》请在冰豆网上搜索。

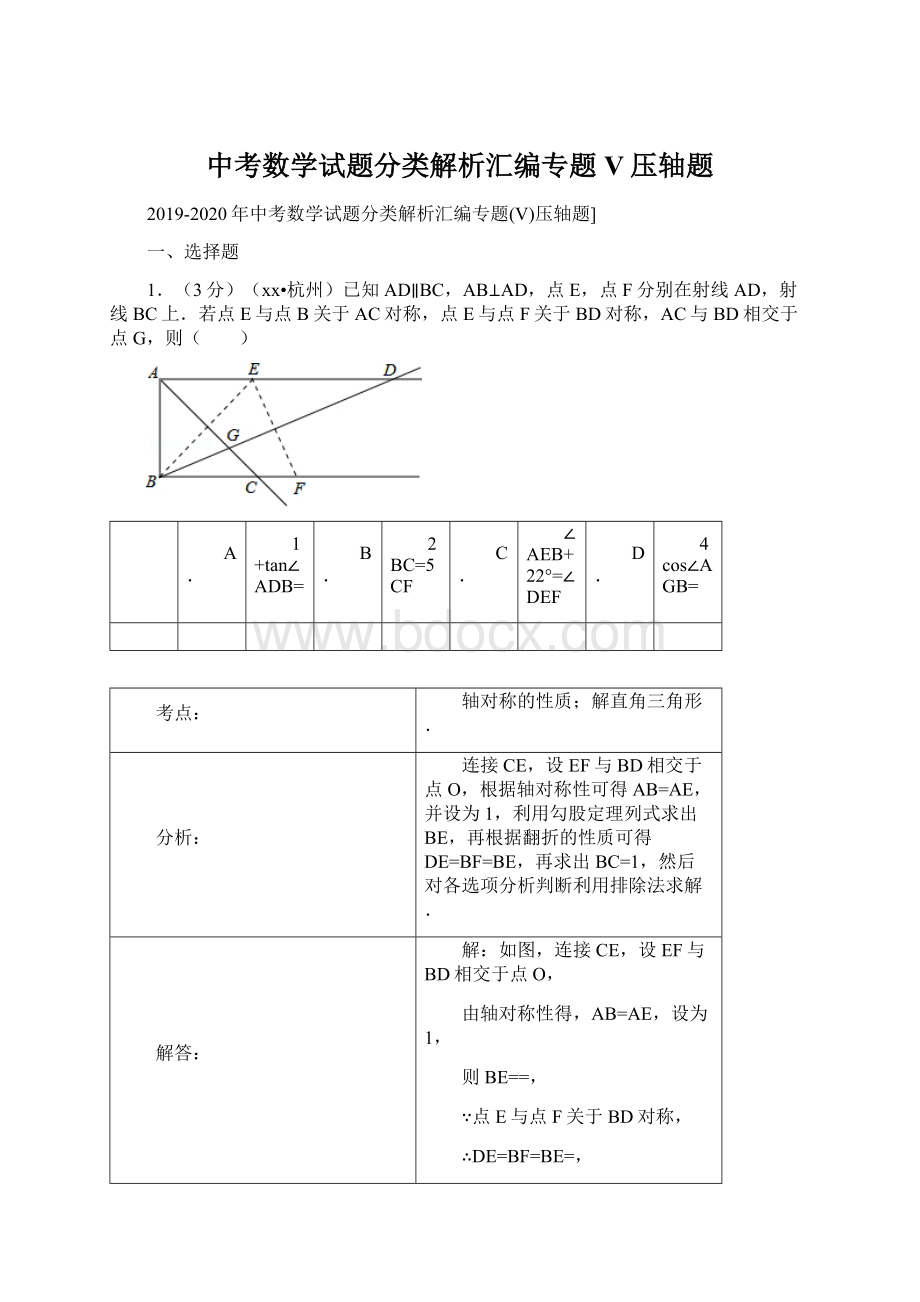
∴四边形ABCE是正方形，

∴BC=AB=1，

1+tan∠ADB=1+=1+﹣1=，故A选项结论正确；

CF=BF﹣BC=﹣1，

∴2BC=2×

1=2，

5CF=5（﹣1），

∴2BC≠5CF，故B选项结论错误；

=45°

+22°

=67°

，

在Rt△ABD中，BD===，

sin∠DEF===，

∴∠DEF≠67°

，故C选项结论错误；

由勾股定理得，OE2=（）2﹣（）2=，

∴OE=，

∵∠EBG+∠AGB=90°

∠EGB+∠BEF=90°

∴∠AGB=∠BEF，

又∵∠BEF=∠DEF，

∴4cos∠AGB==

=，故D选项结论错误．

故选A．

点评：

本题考查了轴对称的性质，解直角三角形，等腰直角三角形的判定与性质，正方形的判定与性质，熟记性质是解题的关键，设出边长为1可使求解过程更容易理解．

二、填空题

1．（xx杭州）射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心，cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值（单位：

秒）

切线的性质；

等边三角形的性质．

专题：

分类讨论．

求出AB=AC=BC=4cm，MN=AC=2cm，∠BMN=∠BNM=∠C=∠A=60°

，分为三种情况：

画出图形，结合图形求出即可；

∵△ABC是等边三角形，

∴AB=AC=BC=AM+MB=4cm，∠A=∠C=∠B=60°

∵QN∥AC，AM=BM．

∴N为BC中点，

∴MN=AC=2cm，∠BMN=∠BNM=∠C=∠A=60°

分为三种情况：

①如图1，

当⊙P切AB于M′时，连接PM′，

则PM′=cm，∠PM′M=90°

∵∠PMM′=∠BMN=60°

∴M′M=1cm，PM=2MM′=2cm，

∴QP=4cm﹣2cm=2cm，

即t=2；

②如图2，

当⊙P于AC切于A点时，连接PA，

则∠CAP=∠APM=90°

，∠PMA=∠BMN=60°

，AP=cm，

∴PM=1cm，

∴QP=4cm﹣1cm=3cm，

即t=3，

当⊙P于AC切于C点时，连接PC，

则∠CP′N=∠ACP′=90°

，∠P′NC=∠BNM=60°

，CP′=cm，

∴P′N=1cm，

∴QP=4cm+2cm+1cm=7cm，

即当3≤t≤7时，⊙P和AC边相切；

③如图1，

当⊙P切BC于N′时，连接PN′3

则PN′=cm，∠PM\N′N=90°

∵∠PNN′=∠BNM=60°

∴N′N=1cm，PN=2NN′=2cm，

∴QP=4cm+2cm+2cm=8cm，

即t=8；

故答案为：

t=2或3≤t≤7或t=8．

本题考查了等边三角形的性质，平行线的性质，勾股定理，含30度角的直角三角形性质，切线的性质的应用，主要考查学生综合运用定理进行计算的能力，注意要进行分类讨论啊．

三、解答题

1．（12分）（xx•杭州）菱形ABCD的对角线AC，BD相交于点O，AC=4，BD=4，动点P在线段BD上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称．设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x．

（1）用含x的代数式分别表示S1，S2；

（2）若S1=S2，求x的值．

四边形综合题；

菱形的性质；

轴对称图形；

特殊角的三角函数值．

综合题；

动点型；

（1）根据对称性确定E、F、G、H都在菱形的边上，由于点P在BO上与点P在OD上求S1和S2的方法不同，因此需分情况讨论．

（2）由S1=S2和S1+S2=8可以求出S1=S2=4．然后在两种情况下分别建立关于x的方程，解方程，结合不同情况下x的范围确定x的值．

（1）①当点P在BO上时，如图1所示．

∵四边形ABCD是菱形，AC=4，BD=4，

∴AC⊥BD，BO=BD=2，AO=AC=2，

且S菱形ABCD=BD•AC=8．

∴tan∠ABO==．

∴∠ABO=60°

．

在Rt△BFP中，

∵∠BFP=90°

，∠FBP=60°

，BP=x，

∴sin∠FBP===sin60°

=．

∴FP=x．

∴BF=．

∵四边形PFBG关于BD对称，

四边形QEDH与四边形PEBG关于AC对称，

∴S△BFP=S△BGP=S△DEQ=S△DHQ．

∴S1=4S△BFP

=4×

×

x•

∴S2=8﹣．

②当点P在OD上时，如图2所示．

∵AB=4，BF=，

∴AF=AB﹣BF=4﹣．

在Rt△AFM中，

∵∠AFM=90°

，∠FAM=30°

，AF=4﹣．

∴tan∠FAM==tan30°

∴FM=（4﹣）．

∴S△AFM=AF•FM

=（4﹣）•（4﹣）

=（4﹣）2．

∴S△AFM=S△AEM=S△CHN=S△CGN．

∴S2=4S△AFM

（4﹣）2

=（x﹣8）2．

∴S1=8﹣S2=8﹣（x﹣8）2．

综上所述：

当点P在BO上时，S1=，S2=8﹣；

当点P在OD上时，S1=8﹣（x﹣8）2，S2=（x﹣8）2．

（2）①当点P在BO上时，0＜x≤2．

∵S1=S2，S1+S2=8，

∴S1=4．

∴S1==4．

解得：

x1=2，x2=﹣2．

∵2＞2，﹣2＜0，

∴当点P在BO上时，S1=S2的情况不存在．

②当点P在OD上时，2＜x≤4．

∴S2=4．

∴S2=（x﹣8）2=4．

x1=8+2，x2=8﹣2．

∵8+2＞4，2＜8﹣2＜4，

∴x=8﹣2．

若S1=S2，则x的值为8﹣2．

本题考查了以菱形为背景的轴对称及轴对称图形的相关知识，考查了菱形的性质、特殊角的三角函数值等知识，还考查了分类讨论的思想．

2．（xx杭州）如图，已知正方形ABCD的边长为4，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=45°

，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1．

（1）求证：

∠APE=∠CFP；

（2）设四边形CMPF的面积为S2，CF=x，．

①求y关于x的函数解析式和自变量x的取值范围，并求出y的最大值；

②当图中两块阴影部分图形关于点P成中心对称时，求y的值．

四边形综合题．

（1）利用正方形与三角形的相关角之间的关系可以证明结论；

（2）本问关键是求出y与x之间的函数解析式．

①首先分别用x表示出S1与S2，然后计算出y与x的函数解析式．这是一个二次函数，求出其最大值；

②注意中心对称、轴对称的几何性质．

（1）证明：

∵∠EPF=45°

∴∠APE+∠FPC=180°

﹣45°

=135°

；

而在△PFC中，由于PF为正方形ABCD的对角线，则∠PCF=45°

则∠CFP+∠FPC=180°

∴∠APE=∠CFP．

（2）解：

①∵∠APE=∠CFP，且∠FCP=∠PAE=45°

∴△APE∽△CPF，则．

而在正方形ABCD中，AC为对角线，则AC=AB=，

又∵P为对称中心，则AP=CP=，

∴AE===．

如图，过点P作PH⊥AB于点H，PG⊥BC于点G，

P为AC中点，则PH∥BC，且PH=BC=2，同理PG=2．

S△APE==×

2×

=，

∵阴影部分关于直线AC轴对称，

∴△APE与△APN也关于直线AC对称，

则S四边形AEPN=2S△APE=；

而S2=2S△PFC=2×

=2x，

∴S1=S正方形ABCD﹣S四边形AEPN﹣S2=16﹣﹣2x，

∴y===+﹣1．

∵E在AB上运动，F在BC上运动，且∠EPF=45°

∴2≤x≤4．

令=a，则y=﹣8a2+8a﹣1，当a==，即x=2时，y取得最大值．

而x=2在x的取值范围内，代入x=2，则y最大=4﹣2﹣1=1．

∴y关于x的函数解析式为：

y=+﹣1（2≤x≤4），y的最大值为1．

②图中两块阴影部分图形关于点P成中心对称，

而此两块图形也关于直线AC成轴对称，则阴影部分图形自身关于直线BD对称，

则EB=BF，即AE=FC，

∴=x，解得x=，

代入x=，得y=﹣2．

本题是代数几何综合题，考查了正方形的性质、相似三角形、二次函数的解析式与最值、几何变换（轴对称与中心对称）、图形面积的计算等知识点，涉及的考点较多，有一定的难度．本题重点与难点在于求出y与x的函数解析式，在计算几何图形面积时涉及大量的计算，需要细心计算避免出错．

3．（xx•杭州）如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°

，AE=3，MN=2．

（1）求∠COB的度数；

（2）求⊙O的半径R；

（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？

你能在其中找出另一个顶点在⊙O上的三角形吗？

请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．

含30度角的直角三角形；

勾股定理；

垂径定理；

平移的性质；

旋转的性质；

相似三角形的判定与性质。

计算题。

（1）由AE与圆O相切，根据切线的性质得到AE与CE垂直，又OB与AT垂直，可得出两直角相等，再由一对对顶角相等，利用两对对应角相等的两三角形相似可得出三角形AEC与三角形OBC相似，根据相似三角形的对应角相等可得出所求的角与∠A相等，由∠A的度数即可求出所求角的度数；

（2）在直角三角形AEC中，由AE及tanA的值，利用锐角三角函数定义求出CE的长，再由OB垂直于MN，由垂径定理得到B为MN的中点，根据MN的长求出MB的长，在直角三角形OBM中，由半径OM=R，及MB的长，利用勾股定理表示出OB的长，在直角三角形OBC中，由表示出OB及cos30°

的值，利用锐角三角函数定义表示出OC，用OE﹣OC=EC列出关于R的方程，求出方程的解得到半径R的值；

（3）把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有6个，如图所示，每小图2个，顶点在圆上的三角形，延长EO与圆交于点D，连接DF，由第二问求出半径，的长直径ED的长，根据ED为直径，利用直径所对的圆周角为直角，得到三角形EFD为直角三角形，由∠FDE为30°

，利用锐角三角函数定义求出DF的长，表示出三角形EFD的周长，再由第二问求出的三角形OBC的三边表示出三角形BOC的周长，即可求出两三角形的周长之比．

（1）∵AE切⊙O于点E，

∴AE⊥CE，又OB⊥AT，

∴∠AEC=∠CBO=90°

又∠BCO=∠ACE，

∴△AEC∽△OBC，又∠A=30°

∴∠COB=∠A=30°

（2）∵AE=3，∠A=30°

∴在Rt△AEC中，tanA=tan30°

=，即EC=AEtan30°

=3，

∵OB⊥MN，∴B为MN的中点，又MN=2，

∴MB=MN=，

连接OM，在△MOB中，OM=R，MB=，

∴OB==，

在△COB中，∠BOC=30°

∵cos∠BOC=cos30°

==，

∴BO=OC，

∴OC=OB=，

又OC+EC=OM=R，

∴R=+3，

整理得：

R2+18R﹣115=0，即（R+23）（R﹣5）=0，

R=﹣23（舍去）或R=5，

则R=5；

（3）在EF同一侧，△COB经过平移、旋转和相似变换后，这样的三角形有6个，

如图，每小图2个，顶点在圆上的三角形，如图所示：

延长EO交圆O于点D，连接DF，如图所示，

∵EF=5，直径ED=10，可得出∠FDE=30°

∴FD=5，

则C△EFD=5+10+5=15+5，

由

（2）可得C△COB=3+，

∴C△EFD：

C△COB=（15+5）：

（3+）=5：

1．

此题考查了切线的性质，垂径定理，勾股定理，相似三角形的判定与性质，含30°

直角三角形的性质，平移及旋转的性质，以及锐角三角函数定义，熟练掌握定理及性质是解本题的关键．