spss实践题分析及答案二docWord下载.docx
《spss实践题分析及答案二docWord下载.docx》由会员分享,可在线阅读,更多相关《spss实践题分析及答案二docWord下载.docx(19页珍藏版)》请在冰豆网上搜索。
.818
398.091
ANOVAb
SumofSquares
df
MeanSquare
F
Sig.
Regression
35250755.672
2
17625377.836
111.218
.000a
Residual
7448393.148
47
158476.450
Total
42699148.820
49
Coefficientsa
UnstandardizedCoefficients
StandardizedCoefficients
t
B
Std.Error
Beta
(Constant)
1304.905
197.655
6.602
.033
.004
.516
8.350
356.296
33.201
.664
10.732
结果分析:
由题目可知客户要求,是根据消费者年收入、家庭人口来预测其每年使用信用卡支付的金额数据,属于多元线性回归问题,其中年收入和家庭人口
看作两个自变量,每年信用卡支付金额看作因变量。
由分析得:
:
信用卡支付金额
年收入
家庭人口
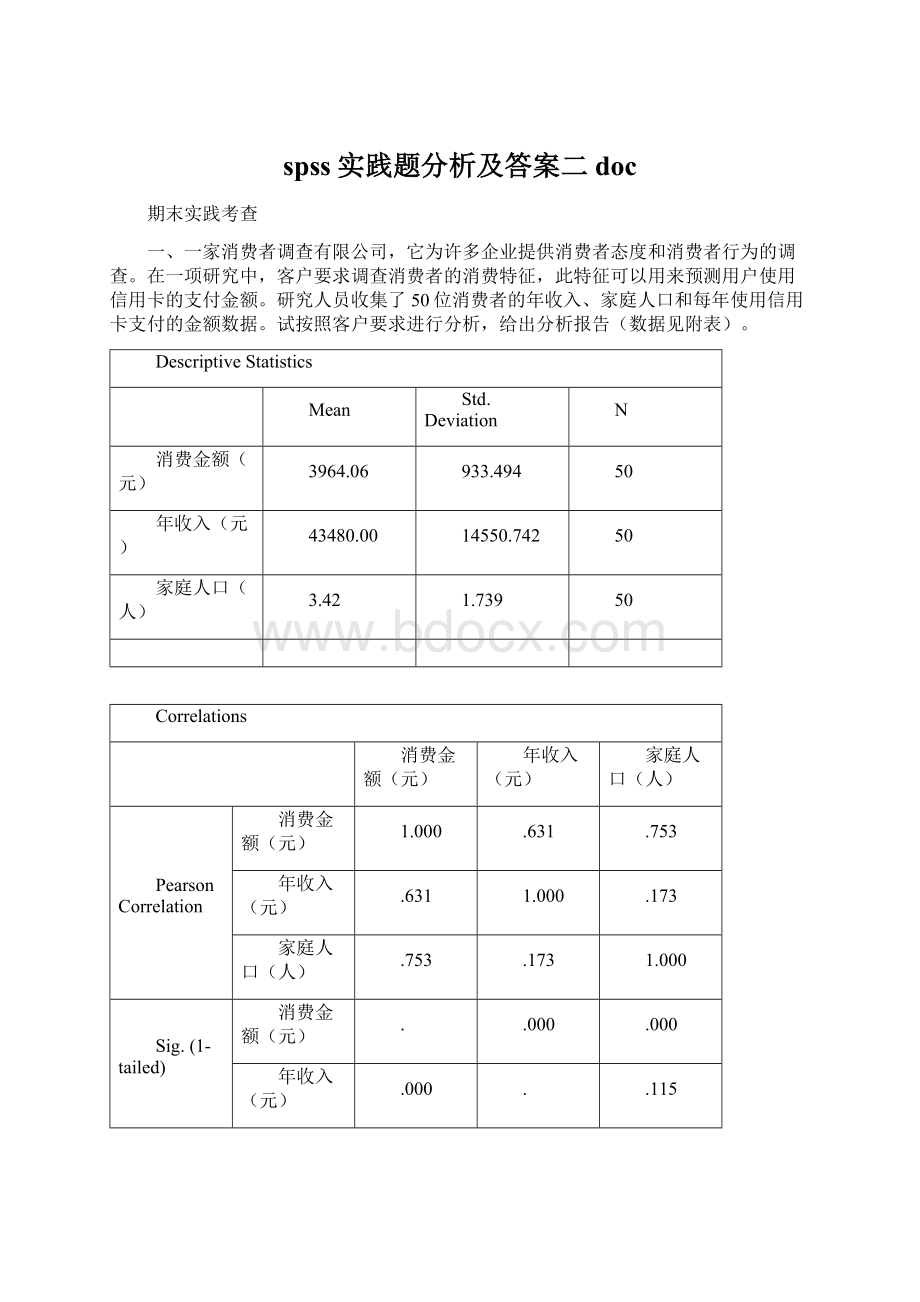
拟合优度检验
为0.818,回归方程能很好的代表样本数据。
回归方程F检验和回归系数T检验的相伴概率都小于显著性水平,拒绝零假设即回归方程和回归系数都具显著型。
二、下表为运动员与大学生的身高(cm)与肺活量(cm3)的数据,考虑到身高与肺活量有关,而一般运动员的身高高于大学生,为进一步分析肺活量的差异是否由于体育锻炼所致,试作控制身高变量的协方差分析,并给出分析报告。
运动员
大学生
身高
肺活量
184.9
167.9
171.0
188.0
179.0
177.0
179.5
187.0
169.0
176.7
183.0
180.5
178.0
164.0
174.0
4300
3850
4100
4800
4000
5400
4500
4780
3700
5250
4250
5000
3600
4050
168.7
170.8
165.0
169.7
171.5
166.5
173.0
173.8
170.5
176.0
169.5
176.3
163.0
172.5
3450
3800
3300
3250
3200
3950
4150
3650
3500
3900
Between-SubjectsFactors
ValueLabel
类别
0
20
1
TestsofBetween-SubjectsEffects
DependentVariable:
Source
TypeIIISumofSquares
CorrectedModel
6981685.135a
3490842.568
22.860
Intercept
208064.290
1.363
.251
1630762.635
10.679
.002
1407847.095
9.220
Error
5649992.365
37
152702.496
6.633E8
40
CorrectedTotal
12631677.500
39
a.RSquared=.553(AdjustedRSquared=.529
控制变量的相伴概率值是0.004,小于显著性水平0.05,因此拒绝零假设,故在剔除身高对肺活量的影响前提下,是否经常进行体育锻炼对肺活量有显著影响;
另外协变量相伴概率为0.002,说明身高的不同水平对肺活量也有显著影响。
三、甲地区为大城市,乙地区为县城,丙地区为农村。
某地分别调查了上述三类地区8岁男生三项身体生长发育指标:
身高、体重和胸围,数据见下表,问:
三类地区之间男生三项身体生长发育指标的差异有无显著性?
试就此问题进行分析并给出分析报告。
由方差齐次性检验表可知,甲乙丙三个地区的的身高、体重和胸围的方差检验相伴概率都大于显著性水平,因此接受零假设,即三个地区的身高、体重和胸围方差相同没有显著性差异,即不同地区,身高、体总和胸围各总体均值服从方差相同的正态分布,因此可以用下面的单因素方差检验。
身高:
相伴概率为0.000小于显著性水平,则各地区身高有显著性差异。
体重:
相伴概率为0.000小于显著性水平,则各地区体重有显著性差异。
胸围:
相伴概率为0.001小于显著性水平,则各地区胸围有显著性差异。
再由LSD,S-N-K和图表分析可知,甲地区(城市)8岁男孩身高和胸围与乙(县城)、丙(农村)地区有显著性差异,乙地区(县城)8岁男孩体重与甲(城市)、丙(农村)地区有显著性差异。
四、某地区10名健康儿童头发和全血中的硒含量(1000ppm)如下,试作发硒与血硒的相关分析,并给出分析报告。
编号
发硒
血硒
3
4
5
6
7
8
9
10
74
66
88
69
91
73
96
58
13
11
16
14
75.40
12.295
10.80
3.327
.872**
Sig.(2-tailed)
.001
由分析可知,要进行发硒和血硒两个定距变量的相关分析。
由上图表可得发硒和血硒的pearson相关系数为0.872,为高度相关。
假设检验得出的相伴概率0.001小于显著水平0.01,因此拒绝零假设,即可以用它们的样本相关系数r代替总体相关系数ρ。
五、某地29名13岁男童身高(cm)、体重(kg)和肺活量(ml)的数据如下表,试对该资料作控制体重影响作用的身高与肺活量相关分析,并给出分析报告。
身高(cm)
体重(kg)
肺活量(ml)
12
15
135.1
139.9
163.6
146.5
156.2
156.4
167.8
149.7
145.0
148.5
165.5
135.0
153.3
152.0
160.5
32.0
30.4
46.2
33.5
37.1
35.5
41.5
31.0
33.0
37.2
49.5
27.6
41.0
47.2
1750
2000
2750
2500
1500
2250
3000
1250
17
18
19
21
22
23
24
25
26
27
28
29
153.0
147.6
157.5
155.1
143.0
149.4
160.8
159.0
158.2
150.0
144.5
154.6
156.5
40.5
43.3
44.7
37.5
31.5
33.9
40.4
38.5
36.0
34.7
39.5
ControlVariables
-none-a
Correlation
.613
.719
Significance(2-tailed)
.588
.337
.079
a.Cellscontainzero-order(Pearson)correlations.
由上表分析可知,体重和肺活量的相关系数为0.613,身高和体重的相关系数为0.719,身高和肺活量的相关系数为0.588,三者之间为中度相关。
身高对体重和肺活量都有影响,剔除它的影响,采用偏相关分析,体重和肺活量相关系数为0.337,为低度相关,相伴概率值为0.079,大于显著性水平0.05,因此接受原假设,即不可以用样本相关系数代替总体相关系数。
六、某医师测得10名3岁儿童的身高(cm)、体重(kg)和体表面积(cm2)资料如下。
试分析“体表面积”可能满足的数学模型,并给出分析报告。
儿童编号
体表面积(Y)
身高(X1)
体重(X2)
5.382
5.299
5.358
5.292
5.602
6.014
5.830
6.102
6.075
6.411
88.0
87.6
88.5
89.0
87.7
89.5
88.8
90.4
90.6
91.2
11.0
11.8
12.0
12.3
13.1
13.7
14.4
14.9
15.2
16.0
.869
.943
.863
体重(X2),身高(X1)
a.Allrequestedvariablesentered.
b.DependentVariable:
体表面积(Y)
.950a
.902
.874
.143346
a.Predictors:
(Constant),体重(X2),身高(X1)
1.321
.661
32.145
.144
.021
1.465
(Constant),体重(X2),身高(X1)b.DependentVariable:
-2.856
6.018
-.475
.649
.069
.075
.215
.919
.389
.184
.057
.758
3.234
.014
由题目要求可知,这是一个多元线性回归问题。
上述图表知,体表面积与身高体重的关系为
其中
体表面积
身高
体重
为0.874,回归方程能很好的代表样本数据。
七、某地1963年调查得儿童年龄(岁)X与锡克试验阴性率(%)Y的资料如下,试分析锡克试验阴性率,并给出分析报告。
年龄(岁)
X
锡克试验阴性率(%)
Y
57.1
76.0
90.9
93.0
96.7
95.6
96.2
ModelDescription
ModelName
MOD_2
DependentVariable
Equation
Inverse
Cubic
Sa
IndependentVariable
年龄
Constant
Included
VariableWhoseValuesLabelObservationsinPlots
Unspecified
ToleranceforEnteringTermsinEquations
.0001
ModelSummaryandParameterEstimates
ModelSummary
ParameterEstimates
df1
df2
b1
b2
b3
.975
198.446
104.380
-48.271
.994
165.373
25.571
37.428
-6.570
.381
S
.983
288.099
4.682
-.639
Theindependentvariableis年龄.
首先由散点图可知,锡克试验阴性率与年龄为非线性关系,因此采用曲线拟合。
由表格可知,最佳拟合曲线为三次曲线(cubic),拟合优度
为0.994,最佳拟合曲线方程为:
:
锡克试验阴性率(%)
八、某单位研究饮食中缺乏维生素E与肝中维生素A含量的关系,将同种属的大白鼠按性别相同,年龄、体重相近者配成对,共8对,并将每对中的两头白鼠随机分到正常饲料组和维生素E缺乏组,过一定时期,测得其肝中维生素A含量。
试分析不同饲料的大白鼠肝中维生素A含量有无差别,给出分析报告(数据见附表)
同种属的大白鼠按性别相同,年龄、体重相近者配成对,该问题属于两配对样本t检验。
由分析得两配对样本t检验的相伴概率值为:
0.004,小于显著性水平0.05,因此拒绝零假设,即大白鼠食物中维生素E的不同含量与肝中维生素A的含量有显著性差异。
九、测得西北某城市1971~2007年1月份平均气温数据(见附表)。
分析该城市90年代前后的温度有无显著差异,给出分析报告。
由于90年代前后1月份平均气温之间相互独立,属于两独立样本t检验的问题。
由分析可得,方差齐次性性F检验的相伴概率是0.438,大于显著性水平0.05,因此接受零假设,即90年代前后方差相同。
t检验相伴概率值为0.002,小于显著性水平0.05,因此拒绝零假设,即该城市90年代前后的温度有显著差异。