计算机组成原理前3章课后习题参考答案解析Word格式文档下载.docx

计算机组成原理前3章课后习题参考答案解析Word格式文档下载.docx

《计算机组成原理前3章课后习题参考答案解析Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《计算机组成原理前3章课后习题参考答案解析Word格式文档下载.docx（20页珍藏版）》请在冰豆网上搜索。

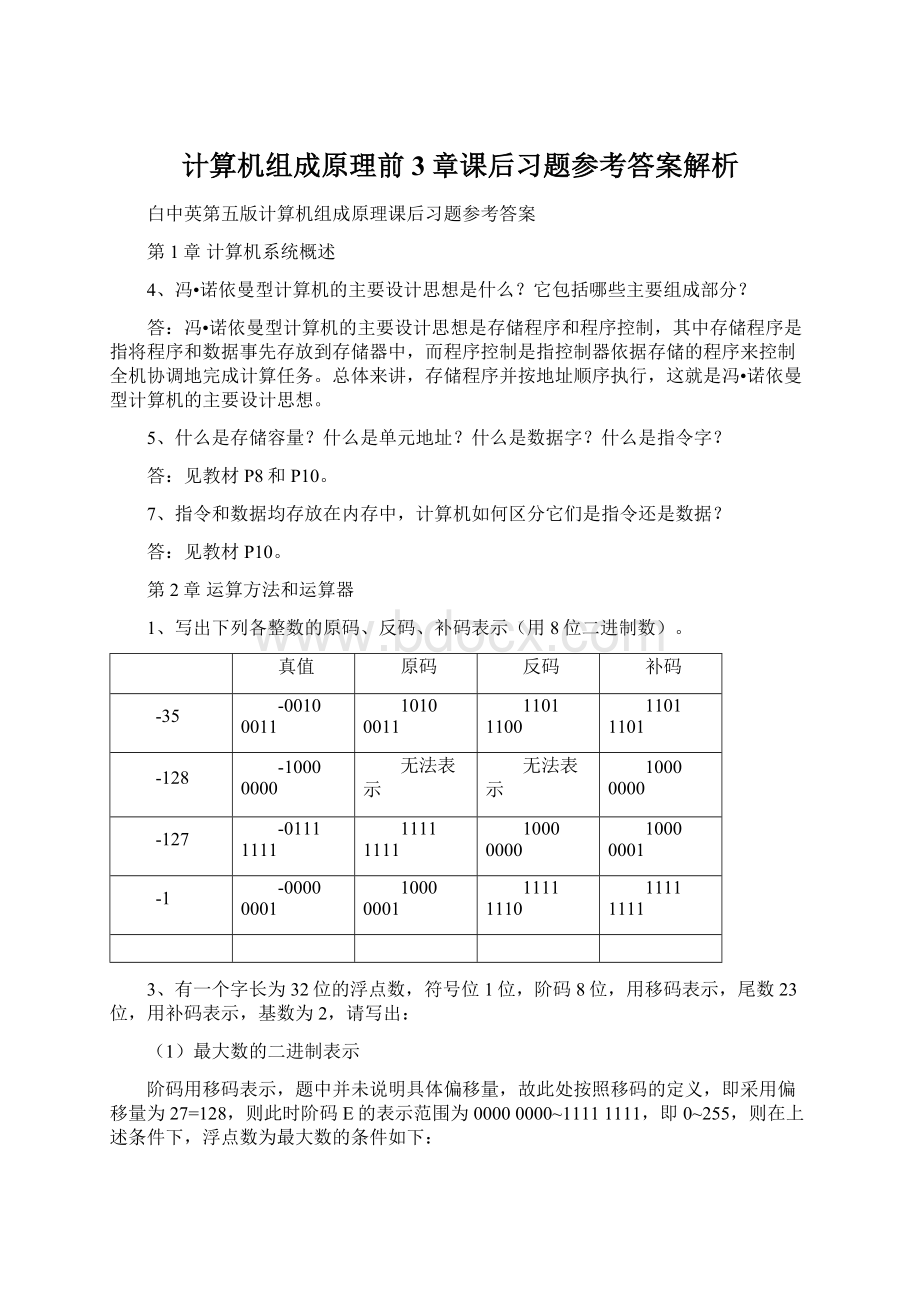
对应十进制真值为：

+（1-2-23）×

2127

（2）最小数的二进制表示

浮点数为最小数的条件如下：

符号S为负

（1）

尾数M最小负数（23）

1

00000000000000000000000

所以最小数的二进制表示为：

11111111100000000000000000000000

-1×

（3）规格化数所表示数的范围

规格化要求尾数若为补码表示，则符号位和最高有效位符号必须不同。

（A）浮点数为最大正数的条件如下：

所以最大正数的二进制表示为：

（B）浮点数为最小正数的条件如下：

阶码E最小（8）

尾数M最小正数（23）

00000000

10000000000000000000000

所以最小正数的二进制表示为：

00000000010000000000000000000000

+2-1×

2-128=+2-129

（C）浮点数为最大负数的条件如下：

尾数M最大负数（23）

01111111111111111111111

所以最大负数的二进制表示为：

00000000001111111111111111111111

-（2-1+2-23）×

2-128

（D）浮点数为最小负数的条件如下：

所以最小负数的二进制表示为：

00000000000000000000000000000000

所以，规格化数所表示数的范围如下：

正数+2-129~+（1-2-23）×

2127负数-2127~-（2-1+2-23）×

4、将下列十进制数表示成IEEE754标准的32位浮点规格化数。

（2）-27/64

解：

-27/64D=-0.011011B=-1.1011×

2-2，则阶码E=-2+127=125，则浮点数为：

符号S

（1）

阶码E（8）

尾数M（23）

01111101

10110000000000000000000

5、已知x和y，用变形补码计算x+y，同时指出结果是否溢出。

（2）x=11011，y=-10101

[x]变补=00,11011，[y]变补=11,01011，则

[x]变补00,11011

+[y]变补11,01011

100,00110

最高进位1丢掉，则[x+y]变补=00,00110，符号位为00，表示结果为正数，且无溢出，即：

x+y=+00110

（3）x=-10110，y=-00001

[x]变补=11,01010，[y]变补=11,11111，则

[x]变补11,01010

+[y]变补11,11111

111,01001

最高进位1丢掉，则[x+y]变补=11,01001，符号位为11，表示结果为负数，且无溢出，即：

x+y=-10111

6、已知x和y，用变形补码计算x-y，同时指出结果是否溢出。

（1）x=11011，y=-11111

[x]变补=00,11011，[y]变补=11,00001，[-y]变补=00,11111，则

+[-y]变补00,11111

01,11010

则[x-y]变补=01,11010，符号位为01，表示结果为正数，且发生正溢。

（2）x=10111，y=11011

[x]变补=00,10111，[y]变补=00,11011，[-y]变补=11,00101，则

[x]变补00,10111

+[-y]变补11,00101

11,11100

则[x-y]变补=11,11100，符号位为11，表示结果为负数，且无溢出，即x-y=-00100。

7、用原码一位乘计算x×

y。

（2）x=-11111，y=-11011

根据原码一位乘的运算规则，乘积的符号位单独处理x0y0，数值部分为绝对值相乘x*.y*，其中数值部分的运算如下：

部分积

乘数

说明

0,00000

+0,11111

11011

部分积初态z0=0

+x*

0,11111

0,01111

11101

右移一位，得z1

1,01110

0,10111

+0,00000

01110

右移一位，得z2

+0

0,01011

10111

右移一位，得z3

1,01010

0,10101

01011

1,10100

0,11010

00101

由上可得，数值部分的乘积为：

x*.y*=0,1101000101，而乘积符号位x0y0=11=0，则[x.y]原=0,1101000101，即x×

y=+1101000101。

8、用加减交替法计算x÷

y（先乘1个比例因子变成小数）。

（2）x=-01011，y=11001

按照加减交替原码除法的运算规则，符号位单独处理x0y0，商值由两数绝对值相除x*/y*求得，且当余数Ri>

0，商1，做2Ri-y*运算，当余数Ri<

0，商0，做2Ri+y*运算。

根据定点除法的约束条件，小（整）数定点机中，被乘数、乘数和商必须均为小（整）数。

而题中被乘数和乘数均为整数，且被乘数小于乘数，两者相除结果为小数，不符合整数定点机的要求，故可先将被乘数和乘数乘以一个比例因子2-5，将被乘数和乘数变为小数，两者相除商也为小数，则符合小数定点机的要求。

乘以比例因子2-5后，可得：

[x]原=1.01011，[y]原=0.11001，[x*]补=0.01011，[y*]补=0.11001，[-y*]补=1.00111，则加减交替法的运算过程如下：

被除数（余数）

商

0.01011

+1.00111

0.00000

+[-y*]补（减除数）

1.10010

1.00100

+0.11001

0

余数为负，商0

左移一位

+[y*]补（加除数）

1.11101

1.11010

00

0.10011

1.00110

001

余数为正，商1

0.01101

0.11010

0011

0.00001

0.00010

00111

00111

1.01001

001110

余数为负，商0（最后一次商0，说明不够减而减了，此处须再恢复余数）

0.0000000010

因余数前后共左移了5次

须右移5次，才得真正余数

由上可得，商值为：

x*/y*=0.01110，而符号位x0y0=10=1，则[x÷

y]原=1.01110，即x÷

y=-0.01110，余数为0.0000000010。

9、设阶码3位，尾数6位，按浮点运算方法，完成下列取值的[x+y]、[x-y]运算。

（2）x=2-101×

（-0.010110），y=2-100×

（0.010110）

[x]补=11,011；

11.101010，[y]补=11,100；

00.010110

（A）求[x+y]

对阶：

[ΔE]补=[Ex]补-[Ey]补=11,011

+00,100

=11,111

由上式可得[ΔE]补=11,111，即阶差为-1，所以Mx-->

1,Ex+1

所以，[x]补’=11,100；

11.110101（0）

尾数求和：

[Mx]补’=11.110101（0）对阶后的尾数[Mx]补’

+[My]补=00.010110

=100.001011（0）

即[x+y]补=11,100；

00.001011，因尾数不符合规格化要求，需左规。

规格化：

尾数左规2次后得：

[x+y]补=11,010；

00.101100

④舍入处理：

采用0舍1入法，因对阶时尾数右移丢0，故可舍去。

⑤溢出判断：

因阶码符号位为11，故浮点数无溢出。

所以最终结果为x+y=+0.101100×

2-110

（B）求[x-y]

+[-My]补=11.101010

=111.011111（0）

即[x-y]补=11,100；

11.011111，尾数符合规格化要求，无需规格化。

无需规格化

所以最终结果为x-y=-0.100001×

2-100

12、用IEEE32位浮点格式表示如下的数：

（2）-1.5

-1.5D=-1.1B=-1.1×

20，所以阶码E=0+127=127，则有：

符号位

（1）

01111111

10000000000000000000000

十六进制表示

BFC00000

（4）1/16

1/16D=0.0001B=1.0×

2-4，所以阶码E=-4+127=123，则有：

01111011

00000000000000000000000

3D800000

13、下列各数使用了IEEE32位浮点格式，相等的十进制数是什么？

（2）00111111010100000000000000000000

根据IEEE32位浮点格式可得，阶码E=01111110=126，则e=126-127=-1，所以浮点数为：

+1.101×

2-1=+0.1101，则对应十进制数为：

0.5+0.25+0.0625=0.8125。

第3章多层次的存储器

1、设有一个具有20位地址和32位字长的存储器，问：

（1）该存储器能存储多少个字节信息？

（220×

32/8=4MB）

（2）如果存储器由512K×

8位SRAM芯片组成，需要多少片？

32/512K×

8=8）

（3）需要多少位地址做芯片选择？

（存储器由20根地址线，而每片芯片有19根地址线，故需1位地址做芯片选择）

3、用16K×

8位的DRAM芯片构成64K×

32位存储器，要求：

（1）画出该存储器的组成逻辑框图。

共需芯片64K×

32/16K×

8=16片，可先用4片16K×

8位的DRAM芯片用于位扩展构成16K×

32位存储器，然后再用4组16K×

32位存储器用于字扩展构成64K×

32位存储器，其中，4组16K×

32位存储器的片选信号由高位地址A15和A14产生，该存储器的组成逻辑框图如下所示。

其中，16K×

32位的存储器的组成逻辑框图如下所示。

（2）设存储器读写周期为0.5μs，CPU在1μs内至少要访问一次。

试问采用哪种刷新方式比较合理？

两次刷新的最大时间间隔是多少？

对全部存储单元刷新一遍所需的实际刷新时间是多少？

5、要求用256K×

16位SRAM芯片设计1024K×

32位的存储器。

SRAM芯片有两个控制端：

当CS’有效时，该片选中。

当W’/R=1时执行读操作，当W’/R=0时执行写操作。

共需SRAM芯片1024K×

32/256K×

16=8片，可先用2片256K×

16位的SRAM芯片用于位扩展构成256K×

32位存储器，然后再用4组256K×

32位存储器用于字扩展构成1024K×

32位存储器，该存储器的组成逻辑框图如下所示。

其中，256K×

6、用32K×

8位的E2PROM芯片组成128K×

16位的只读存储器，试问：

（1）数据寄存器多少位？

（16位）

（2）地址寄存器多少位？

（17位）

（3）共需多少个E2PROM芯片？

（128K×

16/32K×

8=8个）

（4）画出此存储器组成框图。

可先用2片32K×

8位的E2PROM芯片用于位扩展构成32K×

16位存储器，然后再用4组32K×

16位存储器用于字扩展构成128K×

16位存储器，该存储器的组成逻辑框图如下所示。

其中，32K×

16位的存储器的组成逻辑框图如下所示。

7、某机器中，已知配有一个地址空间为0000H~3FFFH的ROM区域。

现在再用一个RAM芯片（8K×

8）形成40K×

16位的RAM区域，起始地址为6000H。

假设RAM芯片有CS’和WE’信号控制端。

CPU的地址总线为A15~A0，数据总线为D15~D0，控制信号为R/W（读/写），MREQ’（访存），要求：

（1）画出地址译码方案。

（2）将ROM和RAM同CPU连接。

RAM区域共需RAM芯片40K×

16/8K×

8=10片，可先用2片8K×

8位的RAM芯片用于位扩展构成8K×

16位存储器，然后再用5组8K×

16位存储器用于字扩展构成40K×

16位存储器，该存储器的组成逻辑框图可参照5、6题。

（A）为了将ROM和RAM同CPU连接，需先将十六进制地址转换为二进制地址码，并确定ROM容量，以及观察ROM和RAM地址码的特点。

A15~A12

A11~A8

A7~A4

A3~A0

0000

ROM，16K×

16

...

0011

1111

0100

空区域

0101

0110

RAM（0）,8K×

2片8K×

8位扩展

0111

1000

RAM

（1）,8K×

1001

1010

RAM

（2）,8K×

1011

1100

RAM（3）,8K×

1101

1110

RAM（4）,8K×

（B）分配CPU地址线：

将CPU的低13位地址A12~A0与ROM和2片8K×

8位RAM的地址线相连。

剩下的高位地址A13~A15与访存信号共同产生芯片的片选信号。

（C）片选信号的形成：

观察上面的地址码发现，当访存信号MREQ’=0，而且高位地址A13~A15为000（或001）、011、100、101、110、111时，分别选择ROM、RAM（0）、RAM

（1）、RAM

（2）、RAM（3）和RAM（4）芯片，故，可采用一个3-8译码器来实现上述片选关系，最后得ROM和RAM与CPU的连接如下图所示。

【说明】上图假设ROM区域由2片8K×

16位芯片进行字扩展构成，若ROM区域由1片16K×

16位芯片构成，则地址线连接会不同。

8、设存储器容量为64M，字长为64位，模块数m=8，分别用顺序和交叉方式进行组织。

存储周期T=100ns，数据总线宽度为64位，总线传送周期τ=50ns。

求：

顺序存储器和交叉存储器的带宽各是多少？

假设连续读出m=8个字，则：

顺序存储器和交叉存储器的数据信息量为：

q=8×

64=512位

顺序存储器所需要的时间为：

t1=m×

T=8×

100ns=800ns=8×

10-7s

故顺序存储器的带宽为：

W1=q/t1=512/（8×

10-7）=64×

107（bit/s）

交叉存储器所需要的时间为t2=T+（m-1）×

τ=100ns+（8-1）×

50ns=450ns=4.5×

故交叉存储器的带宽为W2=q/t2=512/（4.5×

10-7）=113.8×

9、CPU执行一段程序时，cache完成存取的次数为2420次，主存完成存取的次数为80次，已知cache存储周期为40ns，主存存储周期为240ns，求cache/主存系统的效率和平均访问时间。

命中率：

h=Nc/（Nc+Nm）=2420/（2420+80）=0.968

平均访问时间：

ta=htc+tm（1-h）=0.968×

40ns+0.032×

240=46.4ns

cache/主存系统的效率：

e=tc/ta=40/46.4=86.2%

10、已知Cache存储周期为40ns，主存存储周期200ns，Cache/主存系统平均访问时间为50ns，求Cache的命中率为多少？

根据平均访问时间公式ta=htc+（1-h）tm，得：

命中率h=（tm-ta）/（tm-tc）=（200-50）/（200-40）=150/160=0.9375

11、某机器采用四体交叉存储器，今执行一段小循环程序，此程序放在存储器的连续地址单元中。

假设每条指令的执行时间相等，而且不需要到存储器存取数据，请问在下面两种情况中（执行的指令数相等），程序运行的时间是否相等？

（1）循环程序由6条指令组成，重复执行80次；

设总线传送周期为τ，取指周期T，执行指令时间为t，则：

程序运行时间为：

ta=（T+（6-1）τ+6t）×

80

（2）循环程序由8条指令组成，重复执行60次。

ta=（T+（8-1）τ+8t）×

60

13、一个组相联Cache由64个行组成，每组4行。

主存储器包含4K个块，每块128字。

请表示内存地址的格式。

块大小2w=128字=27，故w=7

Cache有64行，每组4行，则组数2d=64/4=16=24，故d=4

主存块数2s=4K=212，故s=12

标记位有s-d=12-4=8位

则组相联映射下的主存地址格式如下：

标记s-d

组号d

块内字号w

8

4

7

14、某机主存容量1MB，字长1B，块大小16B，Cache容量64KB，若Cache采用直接映射方式，请给出2个不同标记的内存地址，它们映射到同一个Cache行。

块大小2w=16B，故w=4

Cache容量64KB，每块16B，行数2r=4K=212，故r=12

主存容量1MB=220=2s+w，故s+w=20，则s=20-w=16，故标记位s-r=16-12=4

直接映射下的主存地址格式如下：

标记s-r

行号r

12

两个满足题目要求的主存地址：

00001001000011100000

00011001000011100000

15、假设主存容量16M×

32位，Cache容量64K×

32位，主存与Cache之间以每块4×

32位大小传送数据，请确定直接映射方式的有关参数，并画出主存地址格式。

块大小2w=4，故w=2

Cache容量64K×

32位，块大小为4×

32位，则行数为2r=64K/4=16K=214，故r=14

主存16M×

32位，则块数2s=16M/4=4M=222，故s=22

标记位s-r=22-14=8位

14

2

19、某虚拟存储器采用页式存储管理，使用LRU页面替换算法。

若每次访问在一个时间单位内完成，页面访问的序列如下：

1，8，1，7，8，2，7，2，1，