整式的乘除与因式分解全章复习与巩固.doc
《整式的乘除与因式分解全章复习与巩固.doc》由会员分享,可在线阅读,更多相关《整式的乘除与因式分解全章复习与巩固.doc(11页珍藏版)》请在冰豆网上搜索。
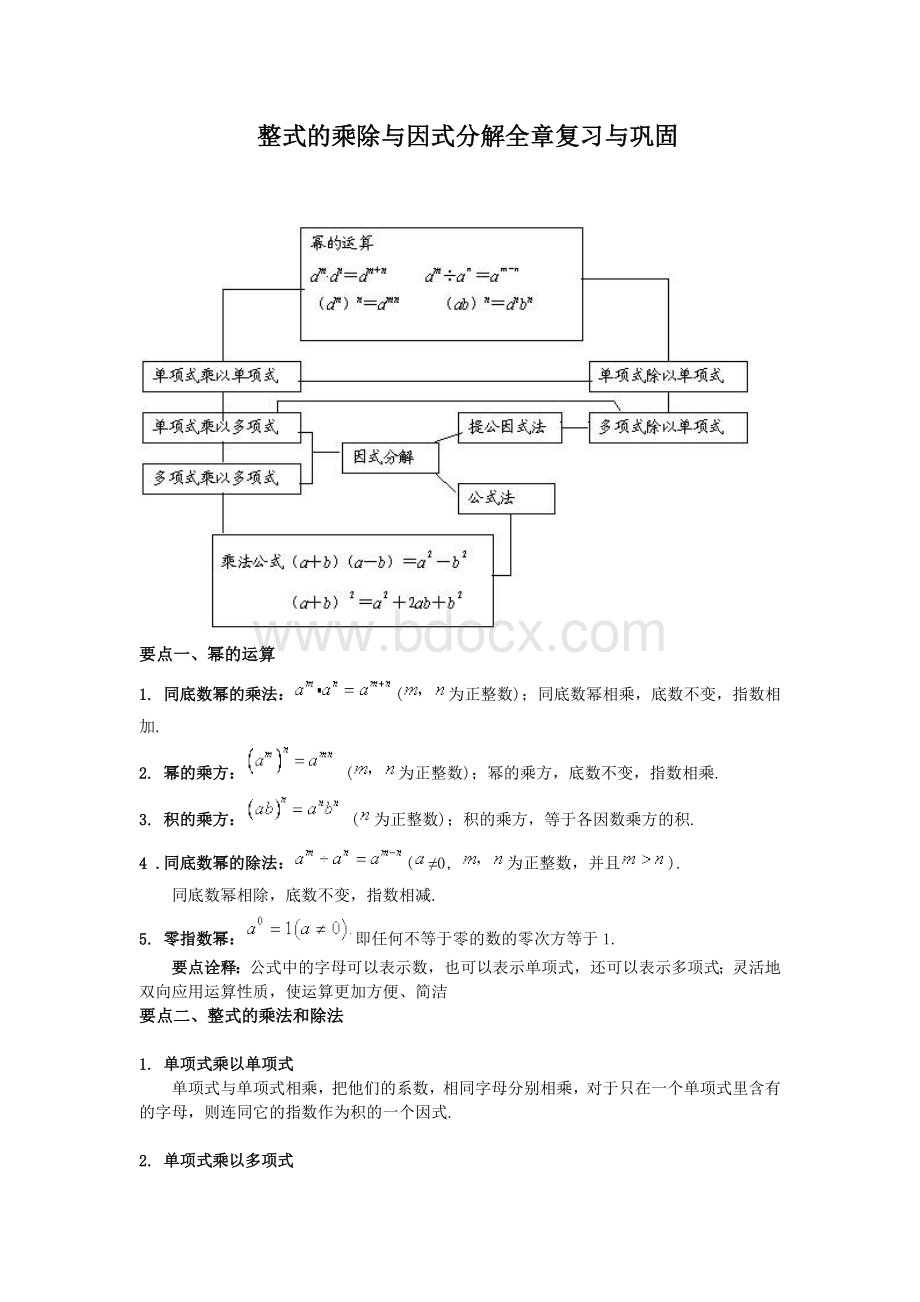
整式的乘除与因式分解全章复习与巩固
要点一、幂的运算
1.同底数幂的乘法:
(为正整数);同底数幂相乘,底数不变,指数相加.
2.幂的乘方:
(为正整数);幂的乘方,底数不变,指数相乘.
3.积的乘方:
(为正整数);积的乘方,等于各因数乘方的积.
4.同底数幂的除法:
(≠0,为正整数,并且).
同底数幂相除,底数不变,指数相减.
5.零指数幂:
即任何不等于零的数的零次方等于1.
要点诠释:
公式中的字母可以表示数,也可以表示单项式,还可以表示多项式;灵活地双向应用运算性质,使运算更加方便、简洁
要点二、整式的乘法和除法
1.单项式乘以单项式
单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
2.单项式乘以多项式
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
即(都是单项式).
3.多项式乘以多项式
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
即.
要点诠释:
运算时,要注意积的符号,多项式中的每一项前面的“+”“-”号是性质符号,单项式乘以多项式各项的结果,要用“+”连结,最后写成省略加号的代数和的形式.根据多项式的乘法,能得出一个应用比较广泛的公式:
.
4.单项式相除
把系数、相同字母的幂分别相除作为商的因式,对于只在被除式里出现的字母,则连同它的指数一起作为商的一个因式
要点三、乘法公式
1.平方差公式:
两个数的和与这两个数的差的积,等于这两个数的平方差.
要点诠释:
在这里,既可以是具体数字,也可以是单项式或多项式.
平方差公式的典型特征:
既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.
2.完全平方公式:
;
两数和(差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍.
要点诠释:
公式特点:
左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍
要点四、因式分解
把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
因式分解的方法主要有:
提公因式法,公式法,分组分解法,十字相乘法,添、拆项法等.
要点诠释:
落实好方法的综合运用:
首先提取公因式,然后考虑用公式;
两项平方或立方,三项完全或十字;
四项以上想分组,分组分得要合适;
几种方法反复试,最后须是连乘式;
因式分解要彻底,一次一次又一次
类型一、幂的运算
1、计算下列各题:
(1)
(2)
(3) (4)
【思路点拨】按顺序进行计算,先算积的乘方,再算幂的乘方,最后算同底数的幂相乘.
【答案与解析】
解:
(1).
(2)
.
(3)
.
(4)
.
【总结升华】在进行幂的运算时,应注意符号问题,尤其要注意系数为-1时“-”号、括号里的“-”号及其与括号外的“-”号的区别
【变式】当,=4时,求代数式的值.
【答案】
解:
类型二、整式的乘除法运算
2、解下列不等式.
(1)
(2)3、已知,
【答案与解析】
解:
(1),
,
.
(2),
.
【总结升华】利用乘法法则进行去括号、合并同类项,按照解一元一次不等式的方法求解求的值.
【变式】
(1)已知,求的值.
(2)已知,,求的值.
(3)已知,,求的值
【思路点拨】利用除法与乘法的互逆关系,通过计算比较系数和相同字母的指数得到的值即可代入求值.
【答案与解析】
解:
由已知,得,
即,,,
解得,,.
所以.
【总结升华】也可以直接做除法,然后比较系数和相同字母的指数得到的值
类型三、乘法公式
4、对任意整数,整式是否是10的倍数?
为什么?
【答案与解析】
解:
∵
,
是10的倍数,∴原式是10的倍数.
【总结升华】
要判断整式是否是10的倍数,应用平方差公式化简后,看是否有因数10.
【变式】解下列方程(组):
【答案】
解:
原方程组化简得,解得
5、已知,,求:
(1);
(2)
【思路点拨】在公式 中能找到 的关系.
【答案与解析】
解:
(1)
∵,,
∴
(2)
∵,,
∴.
【总结升华】在无法直接利用公式的情况下,我们采取“配凑法”进行,通过配凑向公式过渡,架起了已知与未知之间桥梁,顺利到达“彼岸”.在解题时,善于观察,捕捉习题特点,联想公式特征,便易于点燃思维的火花,找到最佳思路
类型四、因式分解
6、分解因式:
(1);
(2).
【答案与解析】
解:
(1).
(2)
.
【总结升华】在提取公因式时要注意提取后各项字母,指数的变化,另外分解要彻底,特别是因式中含有多项式的一定要检验是否能再分,分解因式后可逆过来用整式乘法验证其正确与否
【变式】分解因式:
(1)
(2)
(3)
【答案】
解:
(1)原式
(2)原式=
(3)原式=
巩固练习
一.选择题
1.下列各式从左到右的变化中属于因式分解的是( ).
A. B.
C. D.
2.下列计算正确的是( ).
A. B.
C. D.
3.若是完全平方式,则的值是( )
A.—10 B.10 C.5 D.10或—10
4.将+分解因式,正确的是( )
A. B.
C. D.
5.下列计算正确的是( )
A. B.
C. D.
6.若是的因式,则为( )
A.-15 B.-2 C.8 D.2
7.因式分解的结果是( )
A. B. C. D.
8.下列多项式中能用平方差公式分解的有( )
①;②;③;④;⑤;⑥.
A.1个 B.2个 C.3个 D.4个
二.填空题
9.化简=______.
10.如果是一个完全平方式,那么=______.
11.若,化简=________.
12.若,=__________.
13.把分解因式后是___________.
14.的值是________.
15.当,时,代数式的值是________.
16.下列运算中,结果正确的是___________
①,②,③,④,⑤,
⑥,⑦,
⑧,⑨
三.解答题
17.分解因式:
(1);
(2);
(3).
18.解不等式,并求出符合条件的最小整数解.
19.已知:
,,试用表示下列各式:
(1);
(2);(3).
20.某种液晶电视由于原料价格波动而先后两次调价,有三种方案:
(1)先提价10%,再降价10%;
(2)先降价10%,再提价10%;(3)先提价20%,再降价20%.问三种方案调价的最终结果是否一样?
为什么?
一.选择题
1.【答案】A;
【解析】因式分解是把多项式化成整式乘积的形式.
2.【答案】B;
3.【答案】D;
【解析】
4.【答案】C;
【解析】+==.
5.【答案】B;
【解析】;;.
6.【答案】D;
【解析】.
7.【答案】A
【解析】=.
8.【答案】D;
【解析】③④⑤⑥能用平方差公式分解.
二.填空题
9.【答案】.
10.【答案】±3;
【解析】.
11.【答案】1;
【解析】.
12.【答案】0;
【解析】.
13.【答案】;
【解析】.
14.【答案】-2;
【解析】.
15.【答案】19;
【解析】.
16.【答案】③⑤⑥⑨;
【解析】在整式的运算过程中,符号问题和去括号的问题是最常犯的错误,
要保证不出现符号问题关键在于每一步的运算都要做到有根据,能够用定理法则指导运算.
三.解答题
17.【解析】
解:
(1)=;
(2);
(3).
18.【解析】
解:
符合条件的最小整数解为0,所以.
19.【解析】
解:
(1);
(2);
(3).
20.【解析】
解:
设为原来的价格
(1)由题意得:
(2)由题意得:
(3)由题意得:
.
所以前两种调价方案一样