人教版八年级上学期数学《全等三角形证明》专题练习.doc

人教版八年级上学期数学《全等三角形证明》专题练习.doc

《人教版八年级上学期数学《全等三角形证明》专题练习.doc》由会员分享，可在线阅读，更多相关《人教版八年级上学期数学《全等三角形证明》专题练习.doc（7页珍藏版）》请在冰豆网上搜索。

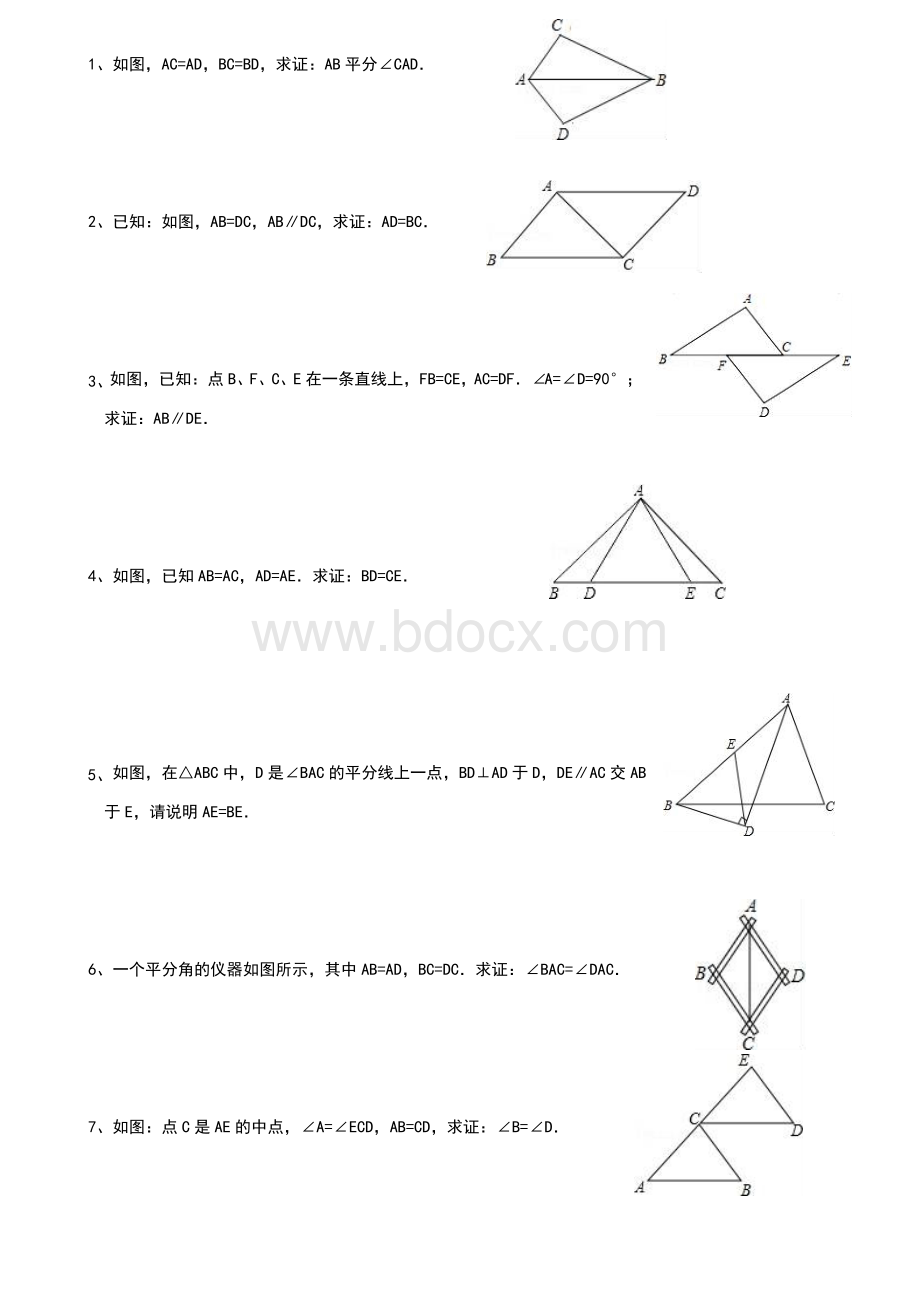
1、如图，AC=AD，BC=BD，求证：

AB平分∠CAD．

2、已知：

如图，AB=DC，AB∥DC，求证：

AD=BC．

3、如图，已知：

点B、F、C、E在一条直线上，FB=CE，AC=DF．∠A=∠D=90°；

求证：

AB∥DE．

4、如图，已知AB=AC，AD=AE．求证：

BD=CE．

5、如图，在△ABC中，D是∠BAC的平分线上一点，BD⊥AD于D，DE∥AC交AB

于E，请说明AE=BE．

6、一个平分角的仪器如图所示，其中AB=AD，BC=DC．求证：

∠BAC=∠DAC．

7、如图：

点C是AE的中点，∠A=∠ECD，AB=CD，求证：

∠B=∠D．

8、如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：

BE=CD．

9、如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．求证：

EC=BF．

10、如图所示，已知AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E，F．试

说明：

AD垂直平分EF．

11、已知：

如图，点E、F在AD上，且AF=DE，∠B=∠C，AB∥DC．求证：

AB=DC．

12、已知：

如图，CB⊥AD，AE⊥DC，垂足分别B、E，AE、BC相交于点F，且AB=BC．

求证：

△ABF≌△CBD．

13、如图所示，已知AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E，F．

试说明：

AD垂直平分EF．

14、如图，在四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，求证：

（1）MD=MB；

（2）MN平分∠DMB．

15、如图，已知，△ABC和△ADE均为等边三角形，BD、CE交于点F．

（1）求证：

BD=CE；

（2）求锐角∠BFC的度数．

16、如图，在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC边上，且BE=CF，BD=CE．

（1）求证：

△DEF是等腰三角形；

（2）当∠A=40°时，求∠DEF的度数；

（3）△DEF可能是等腰直角三角形吗？

为什么？

17、已知：

如图，AB∥CD，AB=CD，点B、E、F、D在同一直线上，∠A=∠C．

求证：

（1）AE=CF；

（2）AE∥CF．

18、如图：

在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF；

说明：

（1）CF=EB．

（2）AB=AF+2EB．

19、如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．求证：

（1）EC=BF；

（2）EC⊥BF．

20、如图1，将一块等腰直角三角板ABC的直角顶点C置于直线l上，图2是由图1抽象出的几何图形，过

A、B两点分别作直线l的垂线，垂足分别为D、E．

（1）求证：

△ACD≌△CBE；

（2）猜想线段AD、BE、DE之间的关系，并说明理由．

21、在△ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC于E，l1与l2相交于点O．△ADE

的周长为6cm．

（1）求BC的长；

（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长．

22、

（1）如图1，∠MAN=90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB=AC，

CF⊥AE于点F，BD⊥AE于点D．求证：

△ABD≌△CAF；

（2）如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是

△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC．求证：

△ABE≌△CAF；

（3）如图3，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．

若△ABC的面积为15，求△ACF与△BDE的面积之和．

23、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

（1）当直线MN绕点C旋转到图1的位置时，求证：

①△ADC≌△CEB；②DE=AD+BE；

（2）当直线MN绕点C旋转到图2的位置时，AD=5，BE=2，求线段DE的长．

24、如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点．

（1）如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．

①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运

动，则经过　　后，点P与点Q第一次在△ABC的　　边上相遇？

（直接写出答案，不必书写解题过程）

25、如图，在正方形ABCD中，AB=BC=CD=AD，∠BAD=∠B=∠C=∠D=90°，点E、F分别在正方形ABCD的边DC、

BC上，AG⊥EF且AG=AB，垂足为G，则：

（1）△ABF与△AGF全等吗？

说明理由；

（2）求∠EAF的度数；

（3）若AG=4，△AEF的面积是6，求△CEF的面积．

26、已知Rt△ABC≌Rt△ADE，其中∠ACB=∠AED=90°．

（1）将这两个三角形按图①方式摆放，使点E落在AB上，DE的延长线交BC于点F．求证：

BF+EF=DE；

（2）改变△ADE的位置，使DE交BC的延长线于点F（如图②），则

（1）中的结论还成立吗？

若成立，加以证明；若不成立，写出此时BF、EF与DE之间的等量关系，并说明理由．