MATLAB语言与控制系统仿真参考答案Word下载.docx
《MATLAB语言与控制系统仿真参考答案Word下载.docx》由会员分享,可在线阅读,更多相关《MATLAB语言与控制系统仿真参考答案Word下载.docx(18页珍藏版)》请在冰豆网上搜索。
d=conv([1.0],conv([1,1],[10,1]));
svs=tf(n.d)
Transferfunction:
10
10sA3+11sA2+s
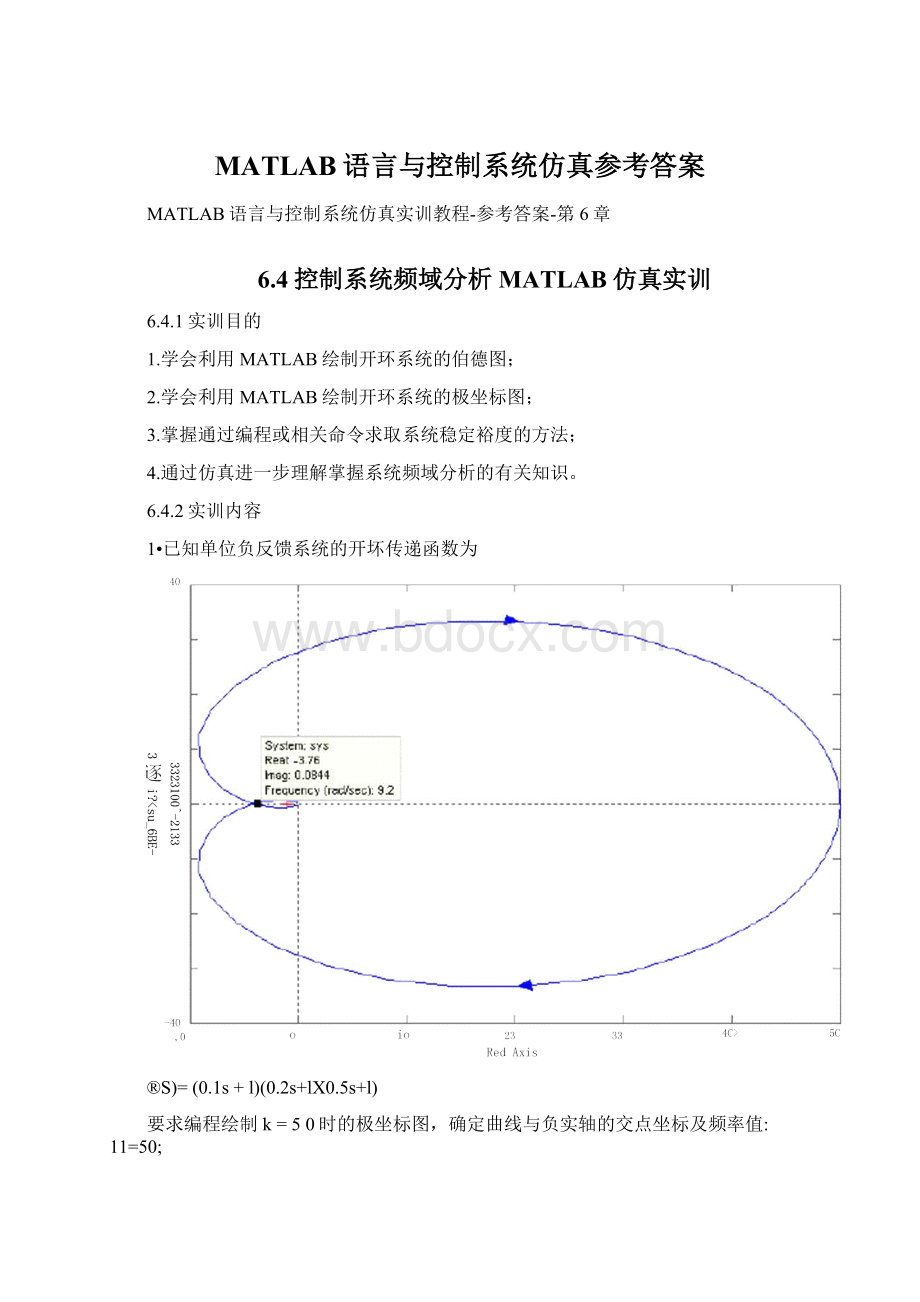
由图上信息可知,幅值裕度为」9・2dB,相角裕度为・34・3度。
(3)G(s)=
8(10s+1)
$(s+lX0・5s+1)
从图上信息可知,幅值裕度为无穷,相角裕度为13.2度。
n=conv([10],[0.0025,0.1,1]);
d=conv([1.0],conv([Ll],[0.1J]));
0.025sA2+s+100.1sA3+1.1sA2+s
niaigm(sys)
Gm=In-f,Pm=18.5deg(at3.05rad/sec)100
ooo
55
-
ooo9
1-
£
3
从图上信息可知,幅值裕度为无穷,相角裕度为18.5度。
3.已知系统开环传递函数
G(s)=('
、
s(2s+1)
(1)试编程绘制系统的BODE图;
n=3;
d=conv([l,0],[2,l]);
2sA2+s
bode(sys)
Frequency(rad/sec)
(2)编写程序,根据程序结果完成下表;
(0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
4⑷
29.42
13.93
8.57
5.86
4.24
3.20
2.49
1.99
1.62
1.34
0(Q)
-101.31
-111.80
-120.96
-128.66
-135.00
-140.19
-144.46
-147.99
-150.95
-153.43
d=conv([l,0],[2J]);
[m,p]=bode(sys,0.1:
0.1:
1.0)m(,J=
m(,2)=
m(,3)=
m(j,4)=
m(,5)=
m(:
\6)=
:
7)=
8)=
m(,9)=
P(:
:
l)=
P(J,2)=
3)=
P(J,4)=
5)=
P(J、6)=
P(J,7)=
8)=
P(J、9)=
PC,:
10)=
4・已知系统开环传递函数
G(s)=戶+1)
、75(0.5s+1X0.1s2+0.25s+1)
试利用bode(sys)命令绘制系统的伯德图(要求带网格线),并通过鼠标在仿真曲线上点击、滑动,在图上找岀相角为-180°
时所对应的频率值©
以及该频率值所对应的分贝数厶(©
)n=[131;
d=conv([L0],conv([0.5J],[0.1,0.25,1]));
bode(sys);
gnd;
50
•100
・45
-50
(HP)孙cd
・270
10'
110J101102
图上相角为一180°
=3.5;
该频率值所对应的分贝数厶(©
)=厶(3.5)=—4・95dB:
5•己知某系统如图6-14所示
图6-14系统的开环传递函数为:
G(s)H(s)=G】
(s)G«
s)=
5(0.15+1)
仿真程序为:
11=2;
d=conv([h0],[0.1,1]);
syso=tf(ii,d);
bode(syso)
(2)求取系统的闭坏传递函数并绘制闭环传递函数的极坐标图,并在图上读取与虚轴交点所对应的频率值。
[nc,dc]=cloop(n,d);
sysc=tf(nc.dc);
nyquist(svsc);
.2O.2
o.o.
-0.4
-0.6
-0.8
NyquistDiagram
System:
sysc
Real:
0.000989
Imag:
-0.445
Frequency(rad/sec):
4.5
•1
-0.8-0.6-0.4-0.200.20.40.60.8
RealAxis
与虚轴交点所对应的频率值为4.5o
6•已知典型二阶系统频域与时域指标间的关系截止频率叫=©
Jjl+铐4一2孑
假设某典型二阶系统©
=10,阻尼系数€[0J],设增量为0.01,试分别绘制截止频
率©
•与§
关系曲线、相角裕量/与§
关系曲线、带宽频率©
,与歹关系曲线。
z=0:
0.01:
l;
wn=10;
wc=wn*sqrt(sqrt(1+4*乙八4)・2*z42);
gania=atan(2*z./sqn(sqil(1+4*z.A4)-2*乙八2));
wb=wn*sqrt((1-2*乙/、2)+sqrt(2・4*乙八2+4*乙八4));
subplot(3JJ);
plot(z,wc);
ylabel(•截止频率工
title(・截止频率与阻尼比关系曲线
subplot(3,l,2);
plot(z,gaina);
ylabel(湘角裕量);
title(湘角裕量与阻尼比关系曲线?
;
gnd;
subplot(3丄3);
plot(z.wb);
ylabelf带宽频率
带宽频率与阻尼比关系曲线?
;
16
14
12
8
6
0010.20.30.40.60.60.70.80.91
7•给定系统
0100
0010
x(r)+
0001
-62.5—213.8-20.42-54
1
“(f)
X=
y=[1562187500]x(/)
求系统的幅值裕量和相角裕量,并画出伯德图。
A=[0JA0:
0Al、o;
oe,oJ卜62・5厂213.8厂20.42厂54];
B=[0:
0;
l];
C=[1562J875,0,0];
D=0;
sys=ss(ABCQ);
maisin(svs)
&
己知系统的开坏传递函数为
绘制系统的Nyquist曲线,并判别闭坏系统的稳定性。
n=20;
d=conv([h6],[lr3]);
sys=tf(nj);
nyquist(svs);
根据奈奎斯特稳定性判据:
对于开坏稳定的系统,闭环系统稳定的充分必要条件是开环系统的奈氏曲线G(je)H(je)不包围(-1J0)点。
反之,则闭环系统是不稳定的。
对于开坏不稳定的系统,有p个开环极点位于右半s平面,则闭环系统稳定的充分必要条件是当㈢:
—8T8变化时,开环系统的奈氏曲线GgHg逆时针包围(一1J0)点P次。
结合本题:
本题开坏不稳定系统,有1个开环极点位于右半s平面,则闭环系统稳定的充分必要条件是当Q:
-8T8变化时,开环系统的奈氏曲线GgHg逆时针包|判
(-1,JO)点1次。
由仿真结果知开环系统的奈氏曲线GgHg逆时针包闱(-1J0)点1次。
所以闭环系统是稳定的。
9己知单位负反馈系统的开坏传递函数为
n=l;
d=conv([l,0],conv([1,1],[0.1,1]));
0.1sA3+1.1sA2+s»
nyquist(sys)
对于开坏稳定的系统,闭环系统稳定的充分必要条件是开环系统的奈氏曲线GgHg不包围(-1J0)点。
对于开坏不稳定的系统,有0个开环极点位于右半s平面,则闭环系统稳定的充分必要条件是当C:
—8T8变化时,开环系统的奈氏曲线GgHg逆时针包围(一1J0)点P次。
对于开坏稳定的系统,闭环系统稳定的充分必要条件是开环系统的奈氏曲线G(je)H(je)不包鬧(-1,八))点。
由仿真结果知开环系统的奈氏曲线GgHg不包鬧(-1J0)点。
所以闭环系统是稳定的。
10.已知系统如图6-15所示,试按照卞表位置关系绘制对应曲线,并求取系统的特征根和相角裕度。
II
1#绘图区域:
输入信号"
(/)曲线
2#绘图区域:
输出信号q(f)曲线
3#绘图区域:
输入信号/•,(/)曲线
4#绘图区域:
输出信号C2(f)曲线
5#绘图区域:
输入信号广3(。
曲线
6#绘图区域:
输出信号5(,)曲线
7#绘图区域:
开环系统伯德图
8#绘图区域:
开坏系统极坐标图
9#绘图区域:
系统单位阶跃响应曲线
10#绘图区域:
系统单位脉冲响应曲线
(1)/;
(r)=cos(5r+45°
)
(2)r2(t)=cos(10f+45°
)(3)^(Z)=cos(15f+45°
)解:
先求出系统的开环传递函数:
22420
—__x
S0.25+15(0.25+1)5(5+5)
no=20;
do=[l,5.0];
[nc,dc]=cloop(no.do);
sys=cloop(no.do)sys=
0020
sys=tf(ncjc)
20
sA2+5s+20»
t=0:
20;
ul=cos(5*t+pi/4);
u2=cos(10*t+pi/4);
u3=cos(15*t+pi/4);
syso=tf(no.do);
subplot(5,2,l);
plot(t,u1);
subplot(5,2,2);
lsim(sys,u1,t);
subplot(5,2,3);
plot(t,u2);
subplot(5,2,4);
lsim(sys,u2,t);
subplot(5,2,5);
plot(tji3);
subplot(5,2,6);
lsim(sys,u3,t);
subplot(5,2,7);
bode(syso);
subplot(5,2,8);
nyquist(syso);
subplot(5,2,9);
step(sys);
subplot(5,2,10);
impulse(sys);
13
rkj
0^03^-QEtf-
unearSimonResults
5IO1531
Tine(sec)
LinearMalionResults
O^D3«
-QEtf-
LinearSmJationResults
Tire(sec)
MyqjistQ8gten
Gap)OO6£
L
•03・0.6-040?
0
Real恥
ImpulseRe^onse
>
」GUImCE・
ri
05
15
225
nun*4
Tire
line(sec)