数值分析实验3Word下载.docx
《数值分析实验3Word下载.docx》由会员分享,可在线阅读,更多相关《数值分析实验3Word下载.docx(15页珍藏版)》请在冰豆网上搜索。
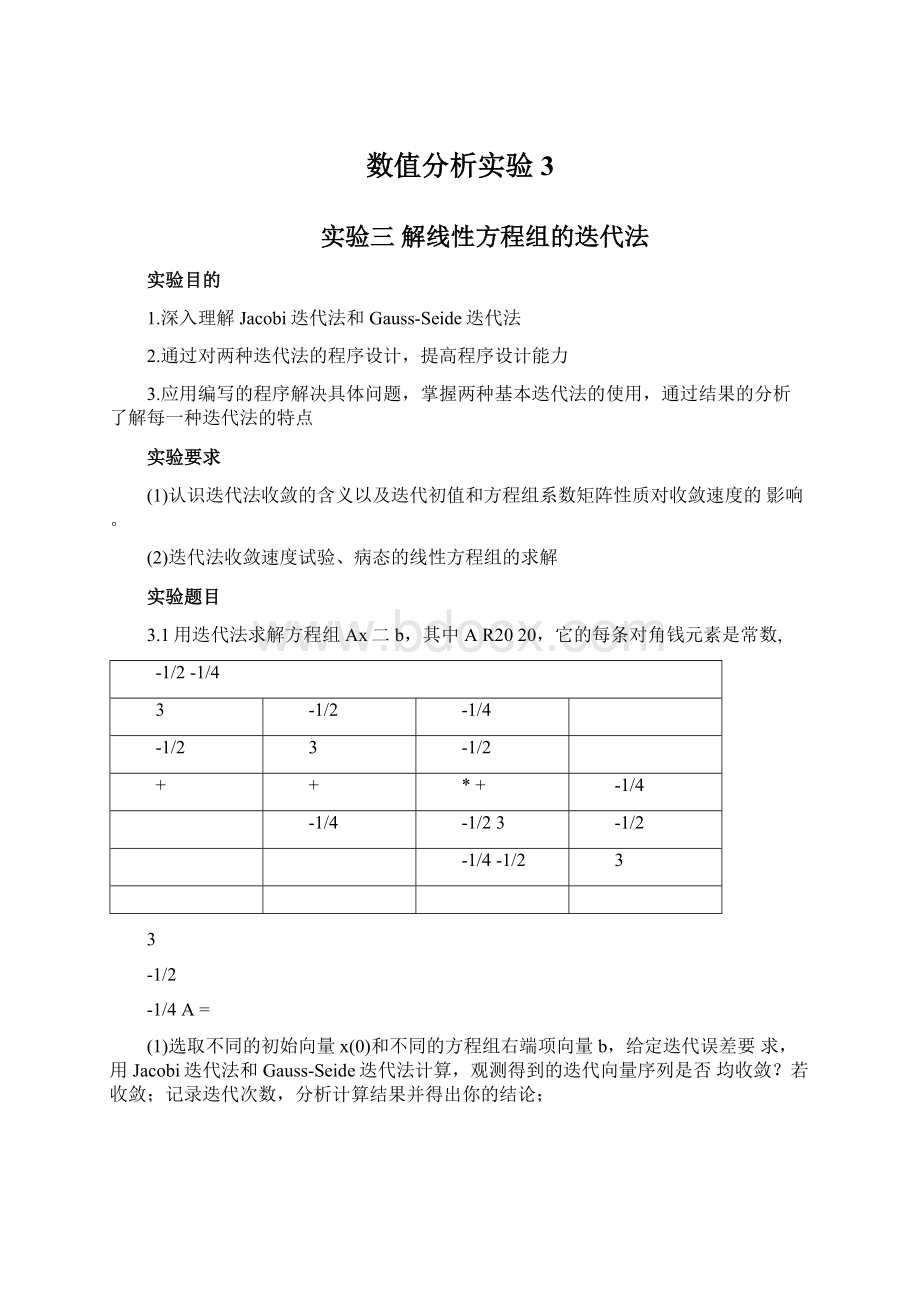
-1/23
-1/4-1/2
-1/4A=
(1)选取不同的初始向量x(0)和不同的方程组右端项向量b,给定迭代误差要求,用Jacobi迭代法和Gauss-Seide迭代法计算,观测得到的迭代向量序列是否均收敛?
若收敛;
记录迭代次数,分析计算结果并得出你的结论;
(2)取定右端向量b和初始向量x(0),将A的主对角线元素成倍增长若干次,非主对角线元素不变,每次用Jacobi迭代法计算,要求迭代误差满足||x(k1)-x(k)||L:
10°
。
比较收敛速度,分析现象并得出你的结论。
(1)1.选取初始向量为x(0)=zeros(20,1),右端向量
b=ones(20,1),eps=1.0e-5;
①实验程序(Jacobi迭代法)
function[x,n]=jacobi(A,b,xO,eps,M)
%A为方程组得系数矩阵
%b为方程组得右端项
%x0为初始向量
%eps为精度要求
%册最大迭代次数
%x为方程组的解
%n为迭代次数
eps=1.0e-5;
%精度要求
M=200;
%最大迭代次数
A=zeros(20,20);
fori=1:
1:
20
A(i,i)=3;
end
forj=1:
ifabs(i-j)==1
A(i,j)=-1/2;
ifabs(i-j)==2
A(i,j)=-1/4;
b=ones(20,1);
x0=zeros(20,1);
D=diag(diag(A));
%取A的对角阵
L=-tril(A,-1);
%取A的下三角阵
U=-triu(A,1);
%取A的上三角阵
B=D\(L+U);
f=D\b;
x=B*xO+f;
n=1;
disp(['
第’,num2str(n),'
步求解结果为:
’]);
disp(x);
whilenorm(x-x0)>
=eps
x0=x;
x=B*x0+f;
n=n+1;
disp(['
if(n>
=M)
disp('
Warning:
迭代次数太多
return;
disp('
最终结果为:
’);
x='
);
n='
num2str(n)]);
实验结果
x=
0.4816
0.5734
0.6328
0.6521
0.6609
0.6643
0.6657
0.6663
0.6665
0.6666
n=18
可能不收敛r);
②实验程序(Gauss-Seide迭代法)
function[x,n]=gauseidel(A,b,x0,eps,M)
%x0为迭代初始向量
Warning:
迭代次数太多,可能不收敛r);
2.选取初始向量为x(0)=zeros(20,1),
右端向量b=1.001*ones(20,1),eps=1.0e-5
修改:
b=1.001*ones(20,1),其余同上
0.4821
0.5740
0.6334
0.6528
0.6616
0.6650
0.6664
0.6669
0.6672
同上
(0)
3.选取初始向量为x=ones(20,1),
右端向量b=ones(20,1),eps=1.0e-5;
1实验程序(Jacobi迭代法)
x(0)=ones(20,1),b=ones(20,1),其余同1
n=17
2实验程序(Gauss-Seide迭代法)
0.4816n=17
结果分析:
不管用哪种迭代法,改变初始向量,右端向量,用有限的迭代次数,都能得到收敛结果且满足误差要求。
(2)取定初始向量为x"
°
)=zeros(20,1),
右端向量b=ones(20,1),eps=1.0e-5
1.A的主对角元素增长为6,用雅克比迭代法:
实验程序
将
(1)1的程序中改为A(i,i)=6;
实验结果最终结果为:
0.1934
0.2103
0.2200
0.2215
0.2221
0.2222
0.1934n=10
2.
12,用雅克比迭代法:
A的主对角元素增长为
0.0892
0.0930
0.0950
0.0952
n=8
3.A的主对角元素增长为
0.0494
0.0506
0.0512
0.0513
n=6
4.A的主对角元素增长为
0.0226
0.0229
0.0230
21,用雅克比迭代法:
45,用雅克比迭代法:
n=5
增大倍数越多,收敛速度越快,但收敛加速度越小。
且最终的解趋
向于0.
心得体会:
通过本次头验,是我加深了对Jacobi迭代法和Gauss—Seidel
迭代法的原理及内在含义的认识、了解和掌握,同时也使我体会到了一些数值计算理论的研究规律,由浅入深,由表及里,由特殊到一般。