学年高中数学32独立性检验的基本思想及其初步应用学案新人教A版Word文档格式.docx

学年高中数学32独立性检验的基本思想及其初步应用学案新人教A版Word文档格式.docx

《学年高中数学32独立性检验的基本思想及其初步应用学案新人教A版Word文档格式.docx》由会员分享，可在线阅读，更多相关《学年高中数学32独立性检验的基本思想及其初步应用学案新人教A版Word文档格式.docx（21页珍藏版）》请在冰豆网上搜索。

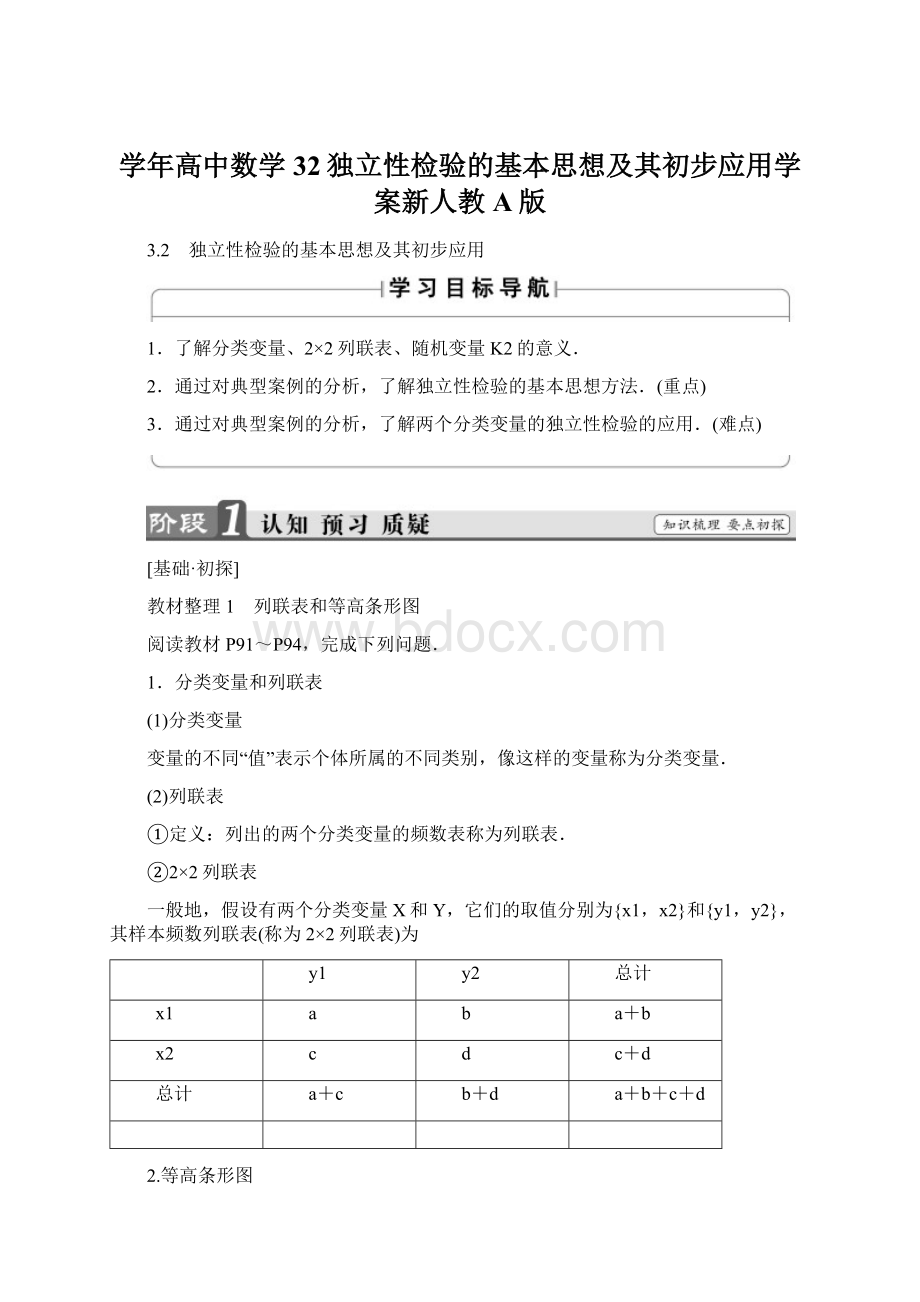
又∵a＋2＝b，∴b＝54.

【答案】　52　54

2．下面的等高条形图可以说明的问题是________（填序号）．

图321

①“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的；

②“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同；

③此等高条形图看不出两种手术有什么不同的地方；

④“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的，但是没有100%的把握．

【答案】　④

3．下列说法正确的有________（填序号）．

①分类变量的取值仅表示个体所属的类别，它们的取值一定是离散的；

②分类变量的取值也可以用数字来表示，但这时的数字除了分类以外没有其他的含义；

③2×

2列联表是两个分类变量的频数汇总统计表；

④2×

2列联表和等高条形图都能反映出两个分类变量间是否相互影响．

【解析】　由分类变量的定义可知①②正确；

由2×

2列联表的定义可知③正确；

2×

2列联表和等高条形图都能展示样本的频率特征，若在一个分类变量所取值的群体中，另一个分类变量所取值的频率相差较小，则说明这两个变量不相互影响，否则就相互影响．故④正确．

【答案】　①②③④

教材整理2　独立性检验

阅读教材P93～P96，完成下列问题．

1．定义

利用随机变量K2来判断“两个分类变量有关系”的方法称为独立性检验．

2．K2＝

，

其中n＝a＋b＋c＋d为样本容量．

3．独立性检验的具体做法

（1）根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上界α，然后查表确定临界值k0.

（2）利用公式计算随机变量K2的观测值k.

（3）如果k≥k0，就推断“X与Y有关系”，这种推断犯错误的概率不超过α；

否则，就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”，或者在样本数据中没有发现足够证据支持结论“X与Y有关系”．

1．若由一个2×

2列联表中的数据计算得K2＝4.013，那么有__________的把握认为两个变量之间有关系．

【解析】　查阅K2表知有95%的把握认为两个变量之间有关系．

【答案】　95%

2．考察棉花种子经过处理与生病之间的关系，得到下表中的数据：

种子处理

种子未处理

得病

32

101

133

不得病

61

213

274

93

314

407

根据以上数据可得出种子是否经过处理与是否生病________（填“有关”或“无关”）.【导学号：

97270061】

【解析】　k＝

≈0.164<

0.455，

即没有充足的理由认为种子是否经过处理跟生病有关．

【答案】　无关

[质疑·

手记]

预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：

疑问1：

解惑：

疑问2：

疑问3：

[小组合作型]

利用等高条形图判断两个分类变量是否相关

　（2016·

青岛高二检测）某学校对高三学生作了一项调查发现：

在平时的模拟考试中，性格内向的学生426人中332人在考前心情紧张，性格外向的学生594人中有213人在考前心情紧张，作出等高条形图，利用图形判断考前心情紧张与性格类别是否有关系．

【精彩点拨】　首先求出在考前心情紧张与考前心情不紧张群体中，性格内向的频率，再绘制等高条形图进行判定．

【自主解答】　作列联表如下：

性格内向

性格外向

考前心情紧张

332

545

考前心情不紧张

94

381

475

426

594

1020

在考前心情紧张的群体中，性格内向的约占61%，在考前心情不紧张的群体中，性格内向的约占20%.绘制相应的等高条形图如图所示：

图中阴影部分表示考前心情紧张与考前心情不紧张中性格内向的比例，从图中可以看出考前心情紧张的样本中性格内向占的比例比考前心情不紧张样本中性格内向占的比例大，可以认为考前紧张与性格类别有关．

利用等高条形图判断两个分类变量是否相关的步骤：

1统计：

收集数据，统计结果.2列表：

列出2×

2列联表，计算频率、粗略估计.3绘图：

绘制等高条形图，直观分析.

[再练一题]

1．网络对现代人的生活影响较大，尤其是对青少年，为了解网络对中学生学习成绩的影响，某地区教育主管部门从辖区初中生中随机抽取了1000人调查，发现其中经常上网的有200人，这200人中有80人期末考试不及格，而另外800人中有120人不及格．利用图形判断学生经常上网与学习成绩是否有关？

【解】　根据题目所给的数据得到如下2×

经常上网

不经常上网

不及格

80

120

200

及格

680

800

1000

得出等高条形图如图所示：

比较图中深色条的高可以发现经常上网不及格的频率明显高于经常上网及格的频率，因此可以认为经常上网与学习成绩有关．

由K2进行独立性检验

　某校高三年级在一次全年级的大型考试中，数学成绩优秀和非优秀的学生中，物理、化学、总分也为优秀的人数如下表所示，则我们能否在犯错误的概率不超过0.001的前提下认为数学成绩优秀与物理、化学优秀有关系？

物理优秀

化学优秀

总分优秀

数学优秀

228

225

267

数学非优秀

143

156

99

注：

该年级此次考试中数学成绩优秀的有360人，非优秀的有880人．

【精彩点拨】　首先分别列出数学成绩与物理、化学、总分的2×

2列联表，再正确计算K2的观测值，然后由K2的值作出判断．

【自主解答】　

（1）根据已知数据列出数学与物理优秀的2×

2列联表如下：

物理非优秀

360

880

371

1240

∴b＝360－228＝132，d＝880－143＝737，b＋d＝132＋737＝869.

代入公式可得K2的观测值为k1≈270.114.

（2）按照上述方法列出数学与化学优秀的2×

化学非优秀

135

724

859

代入公式可得K2的观测值k2≈240.611.

综上，由于K2的观测值都大于10.828，因此说明都能在犯错误的概率不超过0.001的前提下认为数学成绩优秀与物理、化学优秀有关系．

1．利用K2进行独立性检验的步骤

（1）列表：

2列联表．

（2）求值：

求出K2的观测值k.

（3）判断：

与临界值比较，得出事件有关的可能性大小作出判断．

2．独立性检验的必要性

列联表中的数据是样本数据，它只是总体的代表，它具有随机性，所以只能利用列联表的数据和等高条形图粗略判断两个分类变量是否有关系．而K2给出了不同样本容量的数据的统一评判标准．利用它能精确判断两个分类变量是否有关系的可靠程度．

2．在国家未实施西部开发战略前，一新闻单位在应届大学毕业生中随机抽取1000人问卷，只有80人志愿加入西部建设．而国家分步实施西部开发战略后，随机抽取1200名应届大学毕业生问卷，有400人志愿加入国家西部建设．

问：

能否在犯错误的概率不超过0.001的前提下，认为实施西部开发战略的公布对应届大学毕业生的选择产生了影响？

【解】　根据题意，列出2×

志愿者

非志愿者

开发战略公布前

920

开发战略公布后

400

1200

480

1720

2200

由公式计算K2统计量得：

k＝

≈205.22.

因为205.22>

10.828，因此在犯错误的概率不超过0.001的前提下认为实施西部开发战略的公布对应届大学毕业生的选择产生了影响．

[探究共研型]

独立性检验与统计的综合应用

探究1　从容量为400人的中年人与容量为100人的老年人中抽出50人去体检某项健康指标，若采取分层抽样方法，应从中抽取老年人为多少人？

【提示】　

×

100＝10（人）．

探究2　高中流行这样一句话“文科就怕数学不好，理科就怕英语不好”．下表是一次针对高三文科学生的调查所得的数据：

总成绩好

总成绩不好

数学成绩好

478

490

数学成绩不好

399

24

423

913

你能求出a，b，c的值吗？

该问题中有几个分类变量？

它们的取值分别是什么？

【提示】　a＝12，b＝877，c＝36.该问题中有“总成绩”和“数学成绩”两个分类变量；

“总成绩”的取值有“总成绩好”与“总成绩不好”两个值，“数学成绩”的取值也有“好”与“不好”两个值．

探究3　在探究2中，你认为文科学生总成绩不好与数学成绩不好有关系吗？

【提示】　由探究2计算随机变量K2的观测值：

≈6.233>

5.024，

∵P（k≥5.024）≈0.025，

∴在犯错误的概率不超过0.025的前提下，认为文科学生总成绩不好与数学成绩不好有关系．

黄冈高二检测）某企业有两个分厂生产某种零件，按规定内径尺寸（单位：

mm）的值落在[29.94,30.06）的零件为优质品，从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：

甲厂：

分组

[29.86,29.90）

[29.90,29.94）

[29.94,29.98）

[29.98,30.02）

频数

12

63

86

182

[30.02,30.06）

[30.06,30.10）

[30.10,30.14）

92

4

乙厂：

29

71

85

159

76

62

18

（1）试分别估计两个分厂生产零件为优质品的概率；

（2）由以上统计数据填下面2×

2列联表，并问能否有99%的把握认为“两个分厂生产的零件的质量有差异”．

甲厂

乙厂

优质品

非优质品

【精彩点拨】　解答本题先由各组及频数求出优质品的概率，然后完成列联表，最后判断两个变量是否相互独立．

【自主解答】　

（1）甲厂抽查的产品中有360件优质品，从而甲厂生产的零件的优质品率估计为

100%＝72%；

乙厂抽查的产品中有320件优质品，从而乙厂生产的零件的优质品率估计为

100%＝64%.

（2）

320

140

180

500

由表中数据得

≈7.35＞6.635，

因此，有99%的把握认为“两个分厂生产的零件的质量有差异”．

解决独立性检验与统计综合应用的步骤

1．认真审题、弄清所求问题中的两个分类变量是什么，它们的取值分别是什么．

2．充分利用统计知识，完成2×

3．利用独立性检验判断两分类变量间的关系．

3．某学生对其亲属30人的饮食进行了一次调查，并用如图322所示的茎叶图表示30人的饮食指数．（说明：

图中饮食指数低于70的人，饮食以蔬菜为主；

饮食指数高于70的人，饮食以肉类为主）

图322

（1）根据以上数据完成下列2×

主食蔬菜

主食肉类

50岁以下

50岁以上

（2）能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关？

并写出简要分析．

【解】　

（1）2×

8

16

20

10

30

（2）因为K2＝

＝10>

6.635，

P（K2>

6.635）＝0.01，

所以可以在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关．

[构建·

体系]

1．对于分类变量X与Y的随机变量K2的观测值k，下列说法正确的是（　　）

A．k越大，“X与Y有关系”的可信程度越小

B．k越小，“X与Y有关系”的可信程度越小

C．k越接近于0，“X与Y没有关系”的可信程度越小

D．k越大，“X与Y没有关系”的可信程度越大

【解析】　k越大，“X与Y没有关系”的可信程度越小，则“X与Y有关系”的可信程度越大，k越小，“X与Y有关系”的可信程度越小．

【答案】　B

2．下面是调查某地区男女学生喜欢理科的等高条形图，阴影部分表示喜欢理科的百分比，从图323中可以看出（　　）

图323

A．性别与喜欢理科无关

B．女生中喜欢理科的比为80%

C．男生比女生喜欢理科的可能性大些

D．男生不喜欢理科的比为60%

【解析】　由题图知女生中喜欢理科的比为20%，男生不喜欢理科的比为40%，故A，B，D错误，C正确．男生比女生喜欢理科的可能性大些．

【答案】　C

3．在一个2×

2列联表中，由其数据计算得K2＝13.097，认为两个变量有关系犯错误的概率不超过________．

【解析】　如果K2的观测值k>

6.635时，认为“两变量有关系”犯错误的概率不超过0.01.

【答案】　0.01

4．给出下列实际问题：

①一种药物对某种病的治愈率；

②两种药物治疗同一种病是否有区别；

③吸烟者得肺病的概率；

④吸烟人群是否与性别有关系；

⑤网吧与青少年的犯罪是否有关系．

其中用独立性检验可以解决的问题有________．（填序号）【导学号：

97270062】

【解析】　独立性检验主要是对两个分类变量是否有关系进行检验，主要涉及两种变量对同一种事物的影响，或者是两种变量在同一问题上体现的区别等．

【答案】　②④⑤

5．调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据：

出生时间在晚上的男婴为24人，女婴为8人；

出生时间在白天的男婴为31人，女婴为26人．

（1）将下面的2×

2列联表补充完整；

晚上

白天

男婴

女婴

（2）能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系？

【解】　

（1）

31

55

26

34

57

89

（2）由所给数据计算K2的观测值

≈3.689>

2.706.

根据临界值表知P（K2≥2.706）≈0.10.

因此在犯错误的概率不超过0.1的前提下认为婴儿的性别与出生的时间有关系．

我还有这些不足：

（1）　

（2）　

我的课下提升方案：

学业分层测评

（建议用时：

45分钟）

[学业达标]

一、选择题

1．通过对K2的统计量的研究得到了若干个临界值，当K2≤2.706时，我们认为（　　）

A．在犯错误的概率不超过0.05的前提下认为X与Y有关系

B．在犯错误的概率不超过0.01的前提下认为X与Y有关系

C．没有充分理由认为X与Y有关系

D．不能确定

【解析】　∵K2≤2.706，∴没有充分理由认为X与Y有关系．

2．下列关于等高条形图的叙述正确的是（　　）

A．从等高条形图中可以精确地判断两个分类变量是否有关系

B．从等高条形图中可以看出两个变量频数的相对大小

C．从等高条形图中可以粗略地看出两个分类变量是否有关系

D．以上说法都不对

【解析】　在等高条形图中仅能粗略判断两个分类变量的关系，故A错．在等高条形图中仅能够找出频率，无法找出频数，故B错．

3．分类变量X和Y的列联表如下：

则下列说法正确的是（　　）

A．ad－bc越小，说明X与Y关系越弱

B．ad－bc越大，说明X与Y关系越弱

C．（ad－bc）2越大，说明X与Y关系越强

D．（ad－bc）2越接近于0，说明X与Y关系越强

【解析】　对于同一样本，|ad－bc|越小，说明X与Y之间关系越弱；

|ad－bc|越大，说明X与Y之间的关系越强．

4．利用独立性检验对两个分类变量是否有关系进行研究时，若有99.5%的把握认为事件A和B有关系，则具体计算出的数据应该是（　　）

A．k≥6.635　　　　　　B．k<

6.635

C．k≥7.879D．k<

7.879

【解析】　有99.5%的把握认为事件A和B有关系，即犯错误的概率为0.5%，对应的k0的值为7.879，由独立性检验的思想可知应为k≥7.879.

5．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下表的列联表：

男

女

爱好

40

60

不爱好

50

110

由K2＝

算得，

≈7.8.

附表：

P（K2≥k0）

0.050

0.010

0.001

k0

3.841

10.828

参照附表，得到的正确结论是（　　）

A．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

B．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

C．有99%以上的把握认为“爱好该项运动与性别有关”

D．有99%以上的把握认为“爱好该项运动与性别无关”

【解析】　由k≈7.8及P（K2≥6.635）＝0.010可知，在犯错误的概率不超过1%的前提下认为“爱好该项运动与性别有关”，也就是有99%以上的把握认为“爱好该项运动与性别有关”．

二、填空题

6．在对某小学的学生进行吃零食的调查中，得到如下表数据：

吃零食

不吃零食

男学生

女学生

41

39

102

根据上述数据分析，我们得出的K2的观测值k约为________.【导学号：

97270063】

【解析】　由公式可计算得k＝

≈2.334.

【答案】　2.334

7．为了探究电离辐射的剂量与人体的受损程度是否有关，用两种不同剂量的电离辐射照射小白鼠，在照射14天内的结果如表所示：

死亡

存活

第一种剂量

14

11

第二种剂量

6

19

进行统计分析时的统计假设是________．

【解析】　根据独立性检验的基本思想，可知类似于反证法，即要确认“两个分量有关系”这一结论成立的可信程度，首先假设该结论不成立．对于本题，进行统计分析时的统计假设应为“小白鼠的死亡与电离辐射的剂量无关”．

【答案】　小白鼠的死亡与电离辐射的剂量无关

8．在吸烟与患肺病是否相关的判断中，有下面的说法：

①若K2的观测值k>

6.635，则在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；

②从独立性检验可知在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系时，若某人吸烟，则他有99%的可能患有肺病；

③从独立性检验可知在犯错误的概率不超过0.05的前提下，认为吸烟与患肺病有关系时，是指有5%的可能性使得推断错误．

其中说法正确的是________．（填序号）

【解析】　K2是检验吸烟与患肺病相关程度的量，是相关关系，而不是确定关系，是反映有关和无关的概率，故说法①不正确；

说法②中对“确定容许推断犯错误概率的上界”理解错误；

说法③正确．

【答案】　③

三、解答题

9．用两种检验方法对某食品做沙门氏菌检验，结果如下表．

阳性

阴性

荧光抗体法

160

5

165

常规培养法

48

74

186

53

239

附：

0.005

（1）利用图形判断采用荧光抗体法与检验结果呈阳性是否有关系；

（2）能否在犯错误的概率不超过0.001的前提下认为采用荧光抗体法与检验结果呈阳性有关系？

【解】　

（1）作出等高条形图如图所示，由图知采用荧光抗体法与检验结果呈阳性有关系．

（2）通过计算可知K2＝

≈113.1846.而查表可知，因为P（K2≥10.828）≈0.001，而113.1846远大于10.828，所以在犯错误的概率不超过0.001的前提下认为采用荧光抗体法与检验结果呈阳性有关系．

10．有人发现一个有趣的现象，中国人的邮箱里含有数字比较多，而外国人邮箱名称里含有数字比较少，为了研究国籍和邮箱名称里含有数字的关系，他收集了124个邮箱名称，其中中国人的64个，外国人的60个，中国人的邮箱中有43个含数字，外国人的邮箱中有27个含数字．

（1）根据以上数据建立2×

2列联表；

（2）他发现在这组数据中，外国