信号与线性系统分析吴大正第四版第六章习题答案Word文档下载推荐.docx
《信号与线性系统分析吴大正第四版第六章习题答案Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《信号与线性系统分析吴大正第四版第六章习题答案Word文档下载推荐.docx(24页珍藏版)》请在冰豆网上搜索。
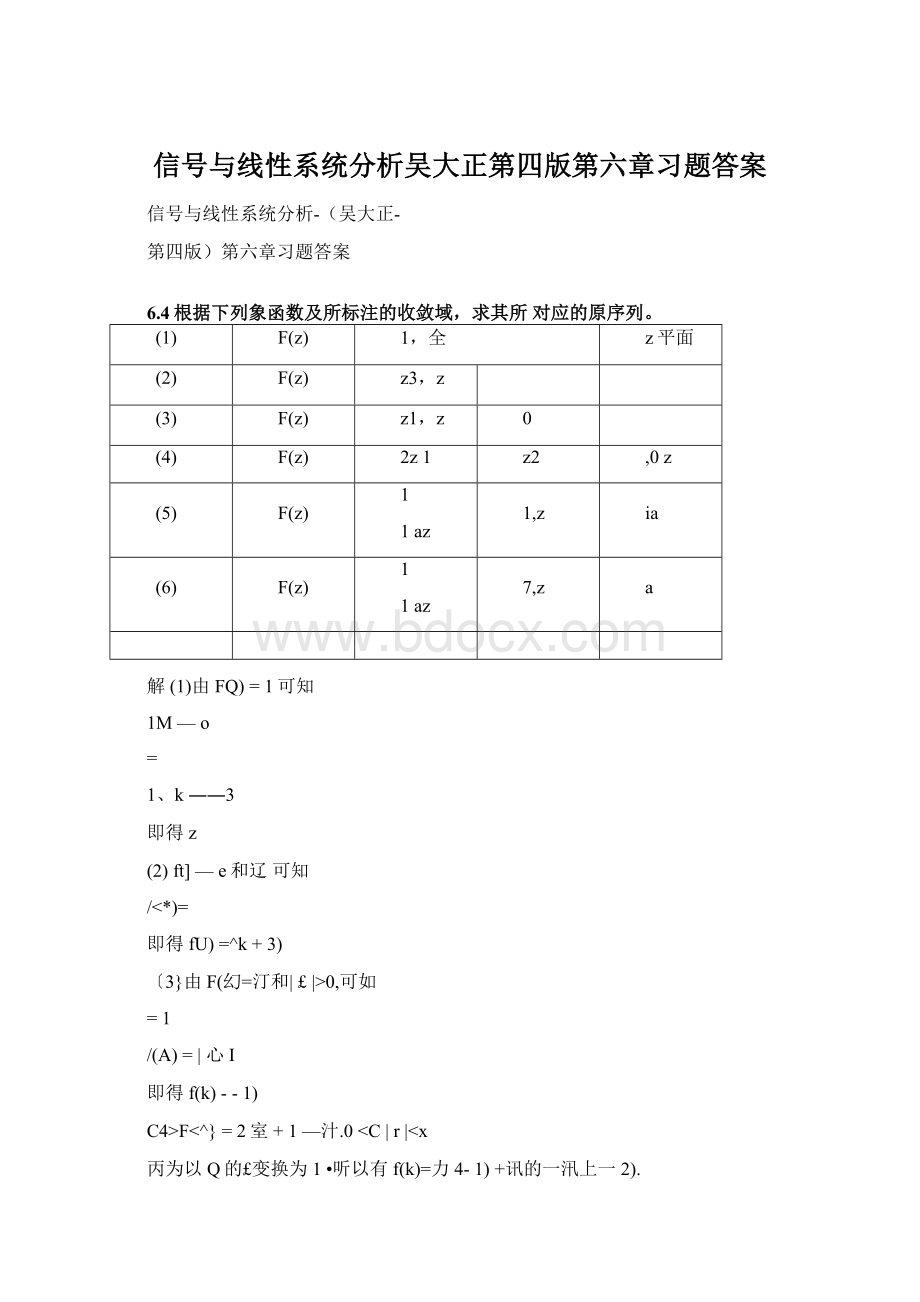
(方)A
(7)f(k)——e(—4)J
=屋d—(k一4)芒(向一4)一4芒(址一4)
1JT-
n-ycos—
jr1一^cos—-|-—
护=2
-r_4e£
+1r+T
6.8若因果序列的z变换f(z)如下,能否应用终值定理?
如果能,求出kimf(k)。
2
縫
(1)尸菇为用果宇列・rtiF(c的表示式可知其收敛域为
(3)f<
k)为因果序列申由Fa)的表示式可知其收敛域为
Ie1>
2
=1不在其收敛域内・则不能应用终值定理求f(^).
6.10求下列象函数的双边逆z变换。
3z
12
(z2)(z1)
艇
(1)由已知可得
F〔门
于是得
收敛域
<
「故/«
)为反因果序列•则可得
f(M=3Tl[F<
^)]=
—3J1—2().€<
—k—
1)
(2)由上题知
FQ)=
11
Z~1Z~1
收敛域Iz>
4■•故/(&
)为殒果序列•则可得
/⑷=旷口
(2)]=[3(畀一2(寺)丁"
)
—凡|心
(2—£
)2(2:
—1)Z1CZ—£
)厶J
K,=(空一1)匕艺
Z
心=#2—当)'
空]
az2z
Kn=(^-4)2F(z)
1Z
F3—4+2*_3:
°
一歹)•
=-3
收敛域I2IV*,故fd)为反因果序列•则可得f(k)=鈔:
[FQ)]=-4e(-^-1)+*虹*)1】£
(_/_1)+
3(y)*e(—Z?
-1)=
=E(^+3)(y)*-4]e(-^-l)
(4)F(z)=
z~
(z-1)
a—1)
K<
Z~1
Ko
+
(乞一i)
d-
・F(£
1JF(z)
z'
—
i
TT
a^=4(t)
_3
f
—3龙+山才
十(z-1)
r
e(—k—1)+3
■4
Q—1)
n3)
6.11求下列象函数的逆
z变换。
(z1)(z
(z1)(z21),z1
(6)F(z)^~^Z,z|a
r1±
I_
:
=8Ck)-—(-j)^+—(j)*C(A)
=5(4)—
t+1
=SCk)—
jsin
K:
老一1w—C
1sin
M)
K“=
卫=—I
C-T
2z(—1)n
z—1寺一"
号
(-IN
*fd—
k)—亡弩gd—e■(-孑)5(A)
2—2cos
e(i)
F(“
a—IF©
十1)
Kn
a_i厂q—i)+k
d-1q
r—1
K.=
■
l)2
丄”一t丄<
-丄厶_
/*FCe)=
・fd=
2a—1卩4s-ii^+i
刍g-厶⑷—亠一1)气⑷
244
-h11,
可一了+了〔_]〉*€(小
丄■(—1严+2及一l]e(i)
4-■
⑹F®
=二_黑=丄•婆土字
(z一a)°
a(z—aK
・fg=—•&
泌⑷
=胪严心)
6.13如因果序列fgf(z),试求下列序列的换。
kk
(1)aif(i)
(2)akf(i)
i0i0
解
(1)由已知•根据E域尺度变换特性•可知
akf(k)F(*)
悵据部分和持性•可得
工扭了(门-^-F<
—)
;
■=—o**—丄a
*k
因f(k)为因果序列,则有2川fe=工町⑺*即有
1=—古
(-Q
1=0
=Fi―)
z—1a
(2)因为f“)为因果字列•则由部分和持性可得
工了⑺=工八门*
i"
Q』■—k
很据工域尺度变换特性可得
亠yFQ)
£
―J
焙心一土吩)
裁乡(切=三吩)
6.15用z变换法解下列齐次差分方程。
(1)y(k)0.9y(k1)0,y
(1)1
(3)y(k2)y(k1)2y(k)0,y(0)0,y
(1)3
解
(1)令y(方)…Y(z).对差分方程取2变换,得
Y(z)—9[疋7YX疋)十》(一1):
=0
可以解得
u、。
・3>
-(—1)
将初始值代入•得
Y(z)=-―£
1—0.9^~1
=<
0<
9〉叫⑷
对上式取逆丸变换,可得
y(k)=ar1LY(x)]
⑶令v(^)—Y(^).对差分方程取賈变换•得
_茫'
丫(零)—v(0)^一y
(1)轩:
一—了(0)茫]—2Y(z)=0
可以解埠
將初始值代入•得
YQ)
4wrr整
7〜■**
工‘—辽—2乞—-疋―I
对卜式取近逆变换■得
列妇=
6.仃描述某LTI离散系统的差分方程为
y(k)y(k1)2y(k2)f(k)
已知y
(1)
1,y
(2)*,f(k)(k),求该系统的零输
入响应yzi(k),零状态响应yzs(k)及全响应y(k)。
+y„(«
(1+£
_-)$(—1)+(—2)I
1一严一2严
将初始狀态及F3=
门—―^代入得
Z—1
~2Z
14
~~2ZTg龙—1z一2
对以上二式仁逆变换-得系统的零输入响应和零狀态响应分别为
J*J
l)(z—1)(^-2)
[Y(i(«
>
]=
_1$
I)*-
-2*•
2、
_Y“(k)_=
L
-1?
-
亠4沪I
.6
~~2
3」
1*
23
yr4)=2f"
]
J-«
2k+—(—1>
*百二6
系统的全『与应
y⑷=兀“)十九〔切=
6.19图6-2为两个LTI离散系统框图,求各系
统的单位序列响应h(k)和阶跃响应g(k)。
A僅)
~r^i—j
3
(o)
nn
解(■该系统在零状态下的空域框图如图右一3亿匚国中延迟单冗(=-)的辎人信号为y^>
.则输出为^-Lr(就儿由加袪棒输出可列出方程
y(el=丄—F(r)
可解得
y<
l)=—FQ1=H<
7)F(i:
豊■=—
系统函散
取逆变换•得系统的单位序列响应
当激励f(k)=心吋,零状态响应前象函数F(z)=迸⑴“)]=
z—d
1,(;
)—H(z)F{z)=[.1[
1z—1?
—11
z——z一—
33
取I■式逆变换•得零状态恥应即阶跃响应
L21141
y(k)=
6.20如图6-2的系统,求激励为下列序列时的零状态响应。
(1)F(z)—
y(?
)=
3—1尸(辽一*)
Y(^)=
3殳丄3z了二1一丁—1
ed)
3I3
2k
(3)F(宅)=—j-
6.23如图6-5所示系统。
(1)求该系统的单位序列响应h(k)。
(2)若输入序列f(k)(y(k),求零状态响应
yzs(k)。
9
m6-5
^y(k)=
冲⑷T
-yz^k)
解
=f"
)-
十心-1)
y2=十⑷T
卜33》(矗1)
Y[(z'
)———tj)Y;
(ar)=——F(ar)
43
1z丄112迄
——
3丄1311
z—z——z一=
6.24图6-6所示系统,
(1)求系统函数H(z);
(2)求单位序列响应h(k);
(3)列写该系统的输入输出差分方程
即
o
式甲系统函数
时的零状态响应为
由右端加法器可列出方程
y(s)=2#g)
由以上两式消去中间变呈XQ停
IkIk
yzs(k)[2(-)2(3)](k)
6.26已知某LTI因果系统在输入f(k)(-)k(k)
4辽
5
D
工
系统模拟框图如图6-12所示。
图6-12
6-29已知某一阶LTI系统,当初始状态y(i)i,
输入fi(k)(k)时,其全响应yi(k)2(k);
当初始
状态y
(1)1,输入f2(k))(k)时,其全响应
差分方程表示为
1彳
yCk)-4ry(k-1)=4/(^)-二和A—1)
■■-O
心)=]+-
2z
2z(2z一
1z
1、
Z一Z
——(
z
求该系统的系统函数H(z),并画出它的模拟框图解丁(怡m=—
y2(k)(k1)(k)。
求输入f(k)(l)k(k)时的零状态响应。
瞩塔虑到零嗡人叽应■一阶I-TI慕统的曇并方理可以写対
5'
j.(^)+n"
—1)=0取上式岸变换*令阳靑)*--*y<
«
?
»
得
(£
}—
当初始伏态为儿(一门=1吋.端人J=g吋+总
y:
1矗)=,(内)一yf(A)=2e(
当初teiss为%n=-1时•输人=+怎“》时■有
3⑷=⑷十孑右"
}=(k—\htk>
対以上芮式私萃变换
・・・1・・e'
Vj(s)—Y,.(J=—■—W{zJF((c)=■-*〒——(1
Fi(«
)=戈』g
丈由12知可得
(s—1)2
则<
1)
(2)两式相加.可得
IKzl
可LJ苓得杀统函数
z——
则可得输入为g时系统零状态响应的象函数
V(上)=F⑶H⑶=—二=二一+—J
11z1.■1T乂一豆(龙_寿)迟_三对上式取逆变换•得系统零状态响应
37(^)=(左+1)(石)e(^)
6.31如图6-10所示的复合系统由3个子系统组成,已知子系统2的单位序列响应h2(k)
(1)k(k),子系统3的系统数出的-Z-,当
7z17
输入f(k)(k)时复合系统的零状态响应y1(k)3(k1)(k)。
求子系统1的单位序列响应h1(k)。
——I人£
<用)卜・
图QIO
解令卢左】*——**——*Y(I)Ji|]Ci}*——*HjC!
r)Ji2(k)-«
——*
一=设子專统1的输人为X4)•由左踹加法黠可列川方程
Xtt)=F(t)+H|(tjHj(r)Ar(5:
1比面FS)
中右竭加法器可列出方囹
ye;
)=xtsmji}
从以上两式中消去中间变量X〔C•可得
3=闇書FZ=叫f]
式中复合累统的祭统闍数
又由已知可得
)=7^7?
对上式取逆变换•得子系统1的单位序列响应
C(A)
6.33设某LTI系统的阶跃响应为g(k),已知当输
入为因果序列f(k)时,其零状态响应
k
yzk(k)g(i)
i0
m_—FC"
〔妇_¥
皐幻-累St圍数为屮…斗域人处
ak}一叙创时•阶紙响应为娜厂.则由卷枳定理得
(j(^)=2飞〔总厂HU=—H(zi
z—I
当績人因果序列/X励时*零状态响应为知4),由卷积定理和部分和性质可得
n=—^心)
5—1
由以上两武可堀得
=F(THQ)
(4—I)-
式中茶统输人闵果序列的象刑数
—7~~—1_^TT7^T
(z—I}'
tZ—I]'
対上式虫逆突凑•谆轿人拥
f(k}=(Jt-kl)f(i)
6.34因果序列f⑹满足方程
f(k)k(k)f(i)
求序列f(k)。
解m―FQ^rti部分和性质可得
一一
士空一i
因f(创为因果序列•故有
Zf®
=工/⑺一WyF®
i—I=—sM空
对已知等式作?
变换,得
F(£
=-__二nrHFO)
(送—1)丄z—1
可解得FQ)=——J
z一1
取逆变换,得因果序列I
f(k)=—w〈k\
6.37移动平均是一种用以滤除噪声的简单数据处理方法。
当接收到输入数据屮)后,就将本次输入数据与其前3次的输入数据(共4个数据)进行平均。
求该数据处理系统的频率响应。
12
解rti已知可得系统输人尹切膚系统的输出为
曲)-
*i=0对上式取空变换.由卷积定理可得
¥
&
)=+工
4
式中系统函数
则系统的顾率响应先
—fF"
1-jijSLI12^
屏414
sin
y(k)为输出。
列出该系统的输入输出差分方程。
问该系统存在频率响应否?
为什么?
(3)若频响函数存在,求输入f(k)20cos(-k30.8)
时系统的稳态响应yss(k)
y\Ck)—f(k一1)一刃(点一1)一0,24力(k—2)
・・・"
)=討窃暮RS
即有〉仆)+了以一1)+0・24了4—2)=2/d—1)+f(k-2)
(2)H(C=»
匚二;
24极点’=一°
・4®
=-°
-5处于单位圆内
・•・该系统存在频率响应
1十2乙
0.24—2十2?
(3)H(z)=
H(“)
1十乃
_1—2j
g号=0.24+j-1j-0.76
=1.78「巾"
=20X1.78cos(今〃+30.8
-63.8°
=35.6cos(-^-k一33c