专题-解析几何知识点汇总(全)资料下载.pdf

专题-解析几何知识点汇总(全)资料下载.pdf

《专题-解析几何知识点汇总(全)资料下载.pdf》由会员分享，可在线阅读，更多相关《专题-解析几何知识点汇总(全)资料下载.pdf（22页珍藏版）》请在冰豆网上搜索。

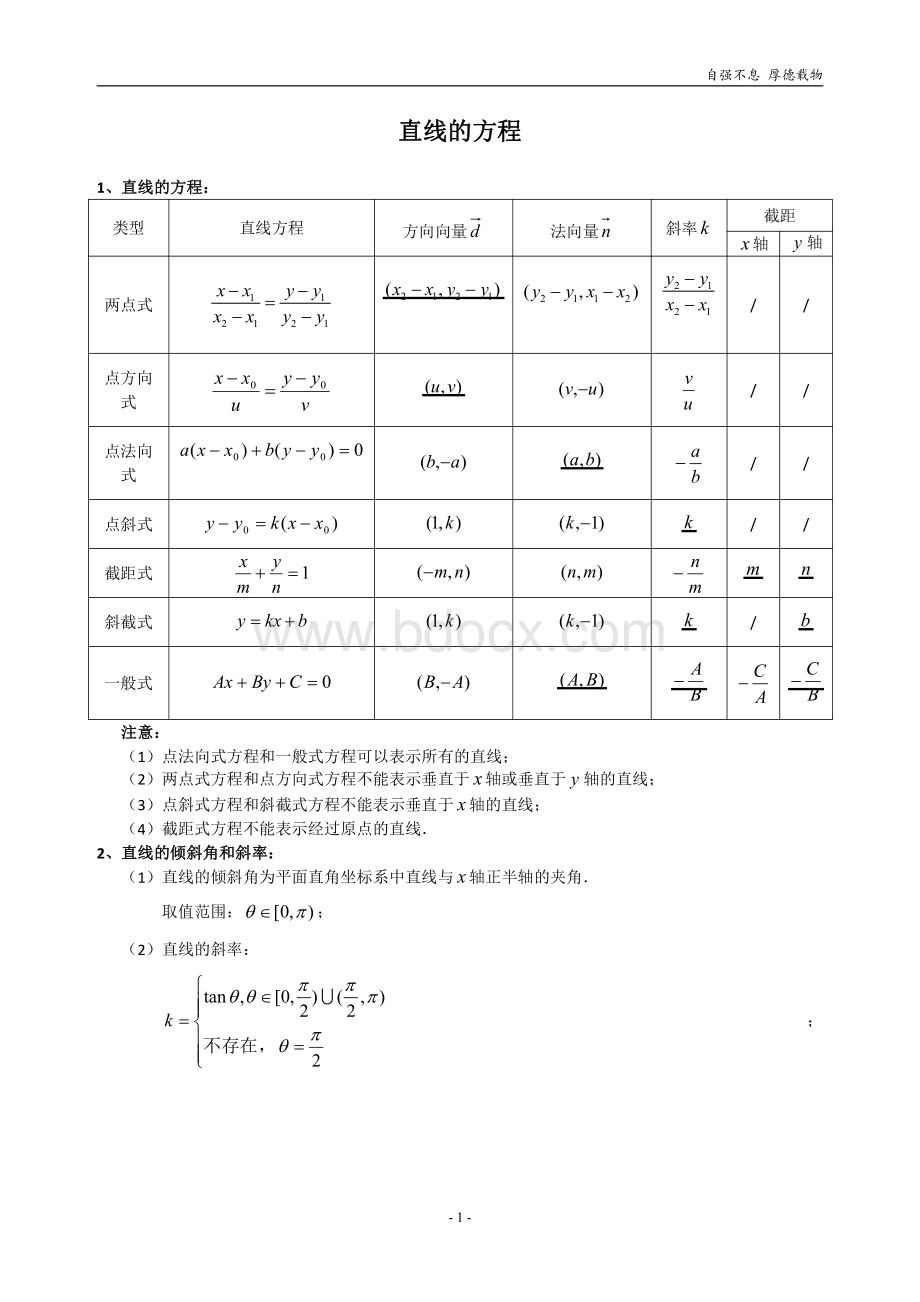
自强不息厚德载物-2-00200tan0,）（,）22202kkkkk在和上单调递增不存在=（3）若直线过点）,（11yx，）,（22yx，则该直线的斜率21211212,xxxxxxyyk不存在，Rk3、两条直线的位置关系：

、两条直线的位置关系：

已知0:

1111cybxal，0:

2222cybxal，则

（1）系数法：

0212121bbaall；

特别地，若1l的斜率为1k，2l的斜率为2k，则12121llkk；

1l与2l相交1221abab；

1l与2l重合111222:

abcabc；

1l与2l平行112211221122:

ababacacbcbc或

（2）向量法：

已知1l的法向量为111（,）nab，2l的法向量为222（,）nab，则12ll120nn12120aabb；

特别地，若1l的斜率为1k，2l的斜率为2k，则12121llkk；

1l与2l相交12nn与不平行1221abab；

1l与2l平行或重合12nn与平行1221abab（3）行列式法：

已知1122abDab，1122xcbDcb，1122yacDac，则11l与2l相交0D；

1l与2l重合0xyDDD；

自强不息厚德载物-3-1l与2l平行0xyDDD、不全为零4、两条相交直线、两条相交直线0:

1111cybxal和0:

2222cybxal的夹角的夹角：

（1）若1l、2l的法向量分别为112（,）nab、222（,）nab，且1l、2l的方向向量分别为1d、2d，则1212122222121122cosnnaabbnnabab或1212cosdddd，0,2；

（2）若1l、2l的斜率分别为1k、2k，且1l到2l的角为1，2l到1l的角为2，则）2,0,1tan2121kkkk；

211211tankkkk，212121tankkkk5、点到直线的距离公式：

、点到直线的距离公式：

（1）点）,（00yxP到直线0:

CByAxl的距离为2200BACByAxd；

（2）直线0:

11CByAxl与直线0:

22CByAxl的距离为2221BACCd6、直线、直线:

0lAxByC同侧同侧/异侧：

异侧：

（1）00000（0）（,）AxByCAPxy在直线:

0（0）lAxByCA的右侧；

00000（0）（,）AxByCAPxy在直线:

0（0）lAxByCA的左侧

（2）点11（,）Mxy、22（,）Nxy在直线l同侧1122（）（）0AxByCAxByC；

点11（,）Mxy、22（,）Nxy在直线l异侧1122（）（）0AxByCAxByC7、点关于直线的对称问题：

、点关于直线的对称问题：

点）,（00yxP直线x轴y轴xyxymxny对称点）,（00yxP）,（00yxP）,（00xyP）,（00xyP）,2（00yxmP）2,（00ynxP自强不息厚德载物-4-补充：

点）,（00yxP关于直线yxb的对称的点为00（,）Pybxb；

点）,（00yxP关于直线yxb的对称的点为00（,）Pbybx；

点）,（00yxP关于直线0AxByC的对称点（,）Pmn满足0000（）（）022AnyBmxmxnyABC或者（,）Pmn，其中0002202,2mxADAxByCDnyBDAB8、三线共点问题：

、三线共点问题：

三条互不平行的直线1111:

0laxbyc，直线2222:

0laxbyc，直线3333:

0laxbyc共点的充要条件是1112223330abcabcabc9、直线系方程：

、直线系方程：

具有某一个共同性质的一簇直线称为直线系

（1）平行直线系：

斜率为0k（常数）的直线系：

0ykxb（b为参数），例：

bxy2；

平行于直线000yBxA的直线系：

）（000为参数CCyBxA

（2）过已知点的直线系：

以斜率k作为参数的直线系：

）（00xxkyy，直线过定点）,（00yx；

0bkxy，直线过定点）,0（0b过两条直线0:

1111CyBxAl，0:

2222CyBxAl的交点的直线系：

）（0）（222111为参数CyBxACyBxA注意：

对于，过定点且平行于y轴或与y轴重合的直线不在直线系内；

对于，其中直线2l不在直线系内10、定直线上动点与两定点距离和差问题：

、定直线上动点与两定点距离和差问题：

（1）定直线上动点与两定点距离和：

问题已知定直线l上动点P，两个定点A、B，求PAPB的取值范围A、B在l的取值范围解答步骤自强不息厚德载物-5-同侧,AB作点A关于l的对称点A；

联结AB，交l于M；

点M为最小值状态点异侧,AB联结AB交l于M；

点M为最小值状态点

（2）定直线上动点与两定点距离差：

问题已知定直线l上动点P，两个定点A、B，点A、B到l的距离分别为1d、2d，直线AB与直线l的夹角为，求PAPB的取值范围A、B在l的1d与2d的大小关系取值范围解答步骤同侧12ddcos,ABAB联结AB并延长交l于M；

点M为最大值状态点12dd,ABAB/12dd,cosABAB联结BA并延长交l于M；

点M为最小值状态点异侧12ddcos,ABAB作点A关于l的对称点A；

联结AB并延长交l于M；

点M为最大值状态点12dd,ABAB/12dd,cosABAB作点A关于l的对称点A；

联结BA并延长交l于M；

2点M为最小值状态点曲线的方程曲线的方程

（一）曲线的方程概论

（一）曲线的方程概论1、轴对称的两个曲线：

、轴对称的两个曲线：

曲线0）,（yxF对称轴x轴y轴xyxymxny曲线0）,（yxF0）,（yxF0）,（xyF0）,（xyF0）,2（yxmF0）2,（ynxF自强不息厚德载物-6-补充：

曲线0）,（yxF关于yxb对称的曲线方程为（,）0Fybxb；

曲线0）,（yxF关于yxb对称的曲线方程为（,）0Fbybx2、中心对称的两个曲线：

、中心对称的两个曲线：

曲线对称中心曲线0）,（yxF）,（nm0）2,2（ynxmF3、轴对称的曲线：

、轴对称的曲线：

曲线0）,（yxF对称轴xyxymxny条件（,）（,）FyxFxy（,）（,）FyxFxy（2,）（,）FmxyFxy（,2）（,）FxnyFxy补充：

（,）（,）FaxyFbxy（,）0Fxy关于2abx对称。

（,）（,）FxayFxby（,）0Fxy关于2aby对称。

（,）（,）FaxyFaxy（,）0Fxy关于xa对称。

（,）（,）FxayFxay（,）0Fxy关于ya对称。

（,）（,）FxyFxy（,）0Fxy关于y轴，即0x对称。

（,）（,）FxyFxy（,）0Fxy关于x轴，即0y对称。

4、中心对称的曲线：

、中心对称的曲线：

曲线0）,（yxF对称轴（,）mn条件（2,2）（,）FmxnyFxy补充：

（,）（,）FaxcyFbxdy（,）0Fxy关于点,22abcd对称。

自强不息厚德载物-7-（,）（,）FaxyFbxy（,）0Fxy关于点,02ab对称。

（,）（,）FxcyFxdy（,）0Fxy关于点0,2cd对称。

（,）（,）FxyFxy（,）0Fxy关于点0,0对称。

5、平移的规律、平移的规律：

“左加右减，下加上减左加右减，下加上减”曲线向左平移k向右平移k向上平移h向下平移h备注0）,（yxF0）,（ykxF0）,（ykxF0）,（hyxF0）,（hyxF0,hk平移向量（,0）k（,0）k（0,）h（0,）h6、伸缩的规律、伸缩的规律：

“倍数与系数互为倒数倍数与系数互为倒数”曲线方程纵坐标不变，横坐标变为原来的倍横坐标不变，纵坐标变为原来的A倍备注（,）0Fxy1（,）0Fxy1（,）0FxyA,0A7、翻折：

、翻折：

曲线翻折后翻折过程0）,（yxF0）,（yxF将0）,（yxF在y轴右边的图像不变，并将其翻折到y轴左边，并覆盖并覆盖y轴左边原来的图像0）,（yxF将0）,（yxF在x轴上边的图像不变，并将其翻折到x轴下边并覆盖并覆盖x轴下边原来的图像0）,（yxF将（,）0Fxy在y轴右边的图像不变，并将其翻折到y轴左边，并覆盖并覆盖y轴左边原来的图像，变换为（,）0Fxy；

将（,）0Fxy在x轴上边的图像不变，并将其翻折到x轴下边，并覆盖并覆盖x轴下边原来的图像，变换为（,）0Fxy

（二）圆的方程

（二）圆的方程1、圆的方程：

、圆的方程：

圆的方程形式圆心坐标半径标准方程222）（）（rbyax）,（bar自强不息厚德载物-8-一般方程022FEyDxyx）2,2（ED2422FED端点方程1212（）（）（）（）0xxxxyyyy其中AB为直径11（,）Axy、22（,）Bxy1212（,）22xxyy221212（）（）2xxyy2、圆的一般方程的判别式：

、圆的一般方程的判别式：

判别式图像轨迹0422FED表示以点）2,2（ED为圆心坐标，以2422FED为圆的半径的圆0422FED表示点）2,2（ED0422FED不表示任何图形3、判断点、判断点00（,）Mxy与圆与圆222）（）（rbyax的位置关系：

的位置关系：

点00（,）Mxy在圆外22200（）（）xaybr点00（,）Mxy在圆上22200（）（）xaybr点00（,）Mxy在圆内22200（）（）xaybr注意：

圆的一般方程亦可使用上述结论4、圆的切线的相关问题：

、圆的切线的相关问题：

（1）过圆222）（）（rbyax上点）,（00yx与圆相切直线方程：

200）（）（rbybyaxax；

（2）过圆022FEyDxyx上点）,（00yx与圆相切直线方程：

0000022xxyyxxyyDEF（3）斜率为k且与圆222xyr相切的切线方程为21ykxrk；

（4）斜率为k且与圆222）（）（rbyax相切的切线方程的求法：

设切线为ykxm，则一般是为0kxym；

利用圆心到切线的距离等于半径，列出方程求m，即21kabmrk（5）当点00（,）Pxy在圆外时，求过点P且与圆222）（）（rbyax相切的切线方程的求法：

自强不息厚德载物-9-可设切线方程为00（）yykxx，利用圆心到直线之间的距离等于半径，即dr，求出k；

或者利用0，求出k；

若求得k只有一值，则还应该有一条斜率不存在，即0xx，此时应补上5、求过圆外给定点作圆的切线的两个切点所在直线：

、求过圆外给定点作圆的切线的两个切点所在直线：

（1）在圆222）（）（rbyax外一点）,（00yx引该圆的两条切线，且两切点为A、B，则AB、两点所在直线的方程：

200）（）（rbybyaxax

（2）在圆022FEyDxyx外一点）,（00yx引该圆的两条切线，且两