北京理工大学电路仿真实验报告Word下载.docx

北京理工大学电路仿真实验报告Word下载.docx

《北京理工大学电路仿真实验报告Word下载.docx》由会员分享，可在线阅读，更多相关《北京理工大学电路仿真实验报告Word下载.docx（22页珍藏版）》请在冰豆网上搜索。

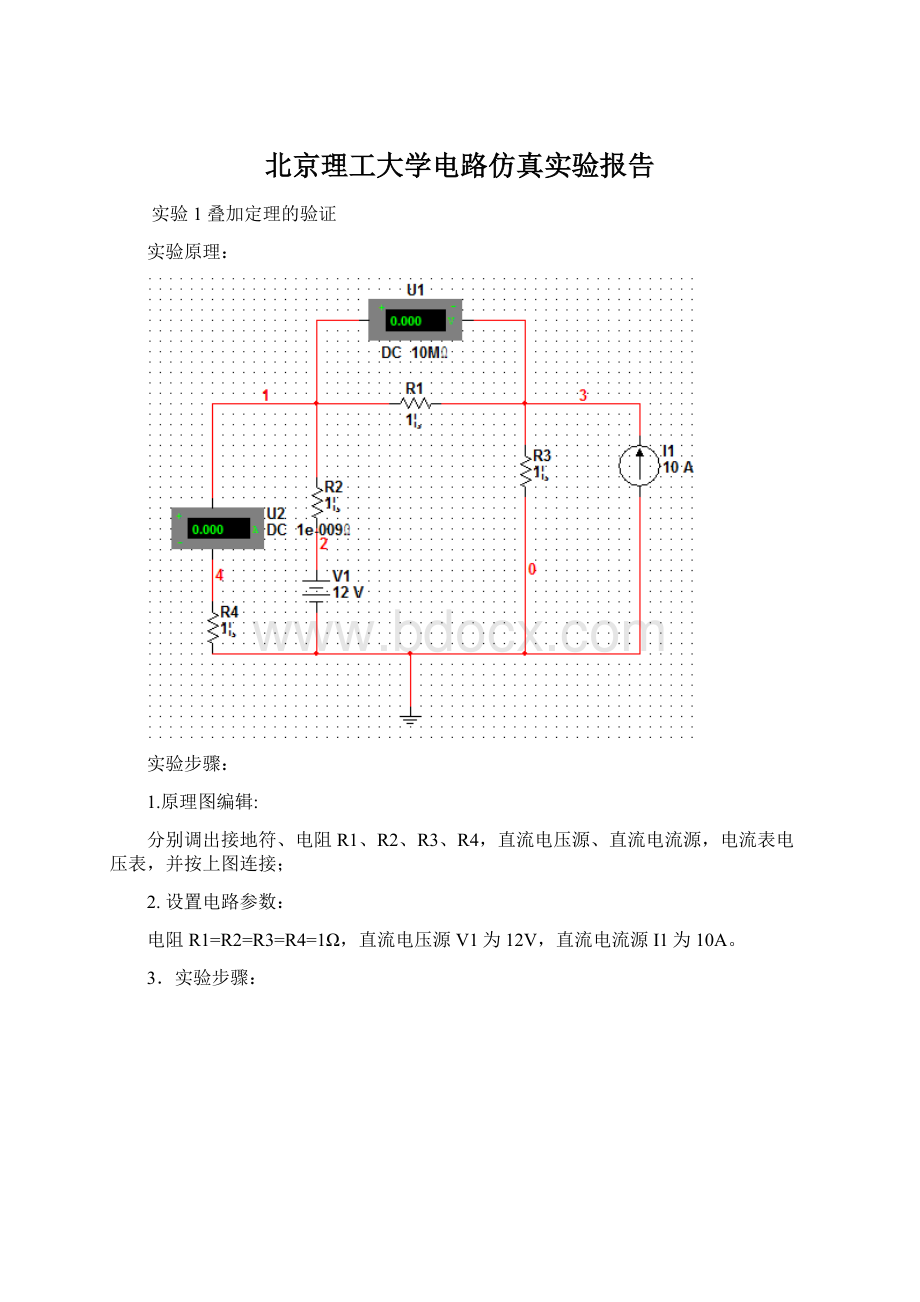
由上式可知，由两个激励产生的响应为每一个激励单独作用时产生的响应之和。

则有，I1=I2+I3

（1）;

同理，U1=U2+U3

（2）.

经检验，6.800=2.000+4.800，-1.600=-4.000+2.400，符合式

（1）、

（2），即叠加原理成立。

实验2并联谐振电路仿真

分别调出电阻R1、R2，电容C1，电感L1，信号源V1；

2.设置电路参数：

电阻R1=10Ω，电阻R2=2KΩ，电感L1=2.5mH,电容C1=40uF。

信号源V1设置为AC=5v，Voff=0，Freqence=500Hz。

3.分析参数设置：

（1）AC分析：

要求：

频率范围1HZ—100MEGHZ，输出节点为Vout。

步骤：

依次选择选择菜单栏里的“simulate->

Analyses->

ACAnalysis”，调出交流分析参数设置对话窗口，起始频率设为1Hz，停止频率设为100MHz，扫描类型为十倍频程，每十倍频程点数设为10，垂直刻度设为线性，其他保持默认，单击“OK”。

然后选择对话框菜单栏的“output”按钮，在左侧的变量中选择“V（out）”,单击“Add”按钮。

这样，交流分析参数设置完毕。

在交流分析参数都设置好以后，单击对话框中的“simulate”按钮，开始仿真，得到如下真结果：

（2）TRAN分析：

分析5个时钟周期的，输出节点为Vout。

步骤：

由信号源的f=500Hz，可得其周期为0.002s。

TransientAnalysis”，调出瞬态分析参数设置对话窗口，起始时间设为0s，结束时间设为5*0.002s=0.01s，其他参数保持默认，单击“OK”。

这样，瞬态分析参数设置完毕。

在参数都设置好以后，单击对话框中的“simulate”按钮，开始仿真，仿真结果如下图所示：

这是并联谐振电路，谐振频率ω0=

此时阻抗模最小，故电容的响应幅度在ω=ω0最大，远离ω0，响应幅度减小，所以在ω=ω0处出现峰值，对应的频率f=ω0/2π=503.5；

实际测量值f=501.4，误差允许范围内，符合理论值。

实验3含运算放大器的比例器仿真

分别调出电阻R1、R2，虚拟运算放大器OPAMP_3T_VIRTUA

调用虚拟仪器函数发生器FunctionGenerator与虚拟示波器Oscilloscope。

电阻R1=1KΩ，电阻R2=5KΩ。

信号源V1设置为Voltage=1v。

函数发生器分别为正弦波信号、方波信号与三角波信号。

频率均为1khz，电压值均为1。

其中方波信号和三角波信号占空比均为50%。

3.分析示波器测量结果：

单击“运行”按钮，电路开始仿真，双击示波器，可以观察到仿真结果，如下：

实验结果：

对于理想运放器，可以等效以下电路图：

列出节点方程：

（G1+G2）u2-G1u1-G2u3=0

由于反相端“虚地”故u2=0

u3=-R2/R1*u1

故u0/us=-5

对应的示波器channelA示数是channelB示数的-5倍；

在误差允许的范围内，实验数据符合这一结论。

实验4二阶电路瞬态仿真

上图中其中C1的电容值分别取1000u,500u.100u.10u，其他参数值如图所示.，并设置初始值为5V，电感L1=1mH，利用multisim软件使用瞬态分析求出上图中各节点的V（out）节点的时域响应,并能通过数据计算出对应电路谐振频率（零输入响应）

2.参数设置：

（1）.参数扫描分析参数设置

ParameterSweepAnalysis”，调出参数扫描分析对话窗口，选择扫描参数的器件类型为“capacitor”，扫描变量类型为“list”，分别将0.001,0.0005,0.0001,1e-005输入选框内。

然后选择对话框菜单栏的“output”按钮，在左侧的变量中选择“V（out）”,单击“Add”按钮，这样，参数扫描分析设置完成。

（2）.瞬态分析参数设置

在参数扫描分析对话窗口的“moreoptions”的“analysistosweep”下拉菜单中选择“transientanalysis”，然后单击“editanalysis”，调出瞬态分析扫描对话框，初始条件设为“user-defined”，起始时间设为0，结束时间设为0.01，单击“OK”，参数设置完毕。

在电路分析参数都设置好以后，单击参数扫描分析对话框的“simulate”按钮，开始仿真，仿真结果如下：

LC电路的零输入响应是按正弦方式变化的等幅振荡，由仿真数据计算得对应的谐振频率如下：

电容C/uF

1000

500

100

10

周期

6.4ms

4.4ms

2.0ms

664.83us

频率/Hz

156.25

227.27

1504.14

ω/（rad/s）

981.75

1428.00

3141.59

9450.82

由角频率表达式

可知，电感大小不变时，

大小与C有关，C越小，

越大，周期越小，振动频率越大。

实验5戴维南等效定理的验证

Figure1

1）分别调出接地符、电阻R，直流电压源电流表电压表，并按Figure1连接运行，并记录电压表和电流表的值；

2）如Figure2连接，将电压源从电路中移除，并使用虚拟一下数字万用表测量电路阻抗；

Figure2电路等效电阻测量

3）如Figure3连接，将电阻RL从电路中移除，并使用电压表测量开路电压；

Figure3电路开路电压值测量

4）如Figure4连接，验证戴维南定理；

Figure4戴维南等效电路图

电阻、电源参数如上述图中所示。

如原理图，分别记录对应电路的电压、电流和电阻值。

计算等效电阻R0：

R0=91+（220||330）=233Ω;

计算开路电压Uoc：

Uoc=220/（220+330）*10=4V;

由戴维南等效电路的知识，figure1与figure4是等效的，故470Ω电阻的电流和电压是相同的。

实验6元件模型参数的并联谐振电路

1.原理图编辑，设置参数：

分别调出电阻R、电感L、电容C和信号源V1（注意区分信号源族和电源族中，交流电压源的区别，信号源的AC设置为5），参数如图所示。

2.参数扫描分析设置：

simulate–>

ParameterSweep：

AC分析设置：

扫描范围1Hz~100MHz,横坐标扫描模式为Decade,纵坐标为线性。

每十倍频程扫描点数为10点，再设置100和1000点并分析所得结果的异同。

观察电容的容值发生变化时，记录电路的幅频响应。

下面依次是每十倍频程扫描点数为10点，100点，1000点的结果：

1.并联谐振电路中，UC=US,品质因数Q=UC/US=1保持不变，故幅度峰值保持不变；

2.通频带

，谐振频率ω0=

可知C越大，ω0越小,BW越小，即通频带越窄。

四条图线（紫，绿，蓝，红）对应的电容C大小依次是4e-004,4e-005,4e-006,4e-007.符合以上分析过程。

四条图线（紫，绿，蓝，红）对应的谐振频率f=ω0/2π，故f理论值分别是159.2Hz，503.5Hz，1592Hz，5035Hz；

下图是分别用光标测得的f0，分别为158.6Hz，502.9Hz，15945Hz，50043Hz。

与理论值吻合较好。

3.

3.每十倍频程扫描点数为10点，100点，1000点的图像形状大致一样，但是扫描点数越大，图像曲线越光滑。

4.AC分析、参数分析的特点

交流分析是在正弦小信号工作条件下的一种频域分析。

它计算电路的幅频特性和相频特性，是一种线性分析方法。

在进行交流频率分析时，首先分析电路的直流工作点，并在直流工作点处对各个非线性元件做线性化处理，得到线性化的交流小信号等效电路，并用交流小信号等效电路计算电路输出交流信号的变化。

参数扫描分析是在用户指定每个参数变化值的情况下，对电路的特性进行分析。

实验7电路过渡过程的仿真分析

分别调出电阻R、电感L、电容C和信号源V1，其中，信号源是Source库SIGNAL_VOLTAGE_SOURCES组中调用PULSE_VOLTAGE，参数如下：

InitialValue1V，PulsedValue0V，DelayTime0s，RiseTime0s，FallTime0s，PulseWidth60μs，Period120μs。

（该电压源用于产生一方波信号）

2.观察电容上的电压波形（使用瞬态分析，分析时间为5倍的方波信号周期），并判断UC（t）的响应属于何种形式（过阻尼/欠阻尼/临界阻尼）？

3.通过计算的电阻的阻值，使用参数分析方法分别观察出其它三种响应形式（过阻尼/欠阻尼/临界阻尼）。

4.电路分析参数设置及电路仿真

瞬态分析参数设置

依次选择选择菜单栏里的“simulate->

TransientAnalysis”，调出瞬态分析参数设置对话窗口，起始时间设为0，结束时间设为5*120us=0.0006s，其他保持默认。

然后选择对话框菜单栏的“output”按钮，在左侧的变量中选择“V（3）”,单击“Add”按钮，这样，瞬态分析参数设置完成。

在电路分析参数都设置好以后，单击“simulate”按钮，开始仿真，得到如下仿真：

下面分别是R等于10000Ω，2000Ω，50Ω时瞬态分析的结果：

1.由临界阻尼

可得，该电路中临近阻尼状态对应的Rd=2000Ω。

则当R=5KΩ时，是过阻尼情形。

2.过阻尼响应形式为：

uc（t）=K1*exp（s1t）+K2*exp（s2t）

临界阻尼响应形式为：

uc（t）=（K1+K2t）*exp（st）

欠阻尼响应形式为：

uc（t）=exp（-αt）*[K1cos（ωdt）+K2sin（ωdt）]

由表达式可知响应波形不同。

3.瞬态分析、参数分析的特点

（1）.瞬态分析是一种非线性时域分析方法，是在给定输入激励信号时，分析电路输出端的