四五年级奥数入门文档格式.docx

四五年级奥数入门文档格式.docx

《四五年级奥数入门文档格式.docx》由会员分享，可在线阅读，更多相关《四五年级奥数入门文档格式.docx（24页珍藏版）》请在冰豆网上搜索。

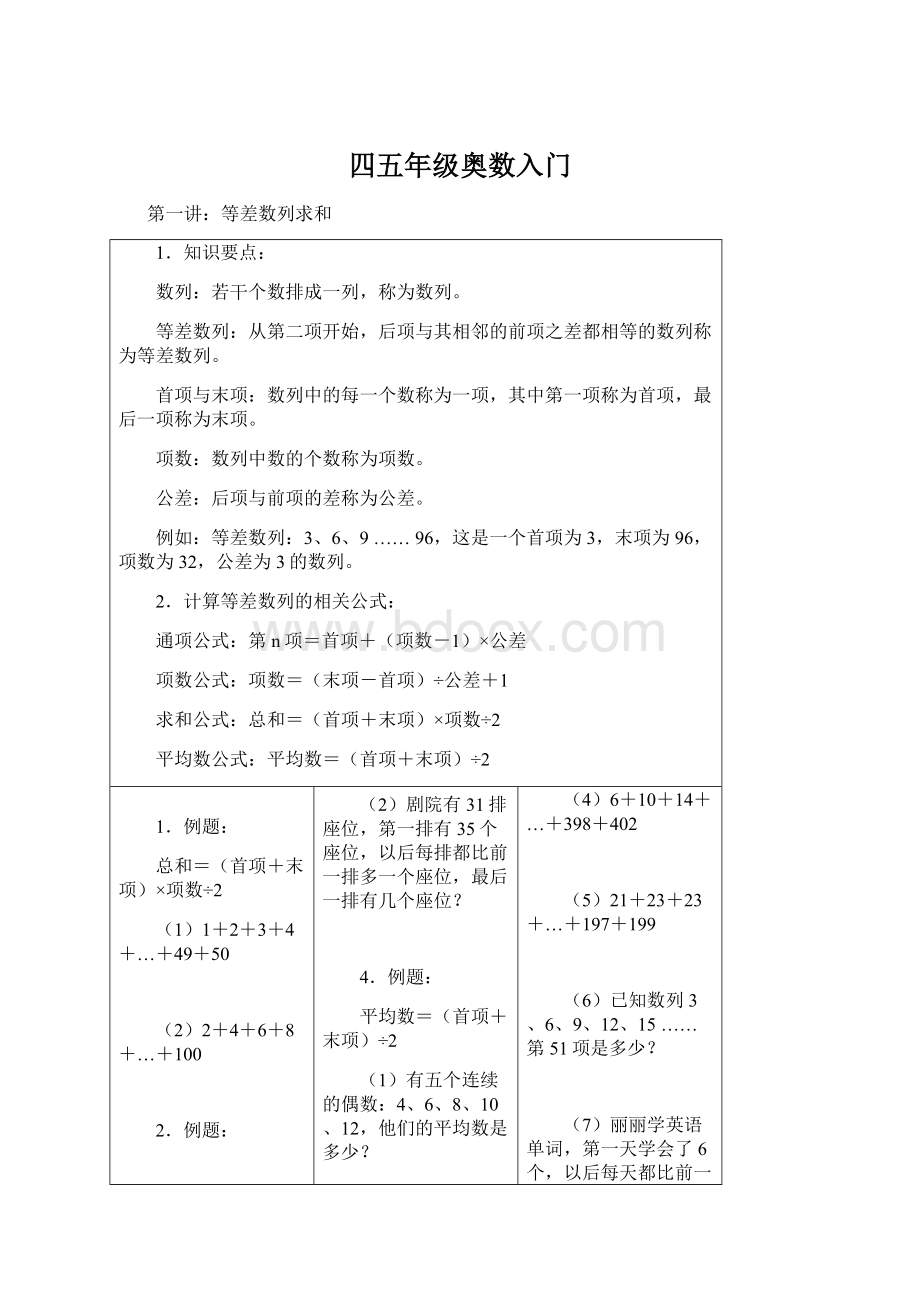
平均数公式：

平均数＝（首项＋末项）÷

1．例题：

（1）1＋2＋3＋4＋…＋49＋50

（2）2＋4＋6＋8＋…＋100

2．例题：

（1）已知数列2、5、8、11、14……，47应该是其中的第几项？

（2）3＋6＋9＋12＋…＋33＋36

3．例题：

（1）已知数列2、5、8、11、14……，第21项是多少？

（2）剧院有31排座位，第一排有35个座位，以后每排都比前一排多一个座位，最后一排有几个座位？

4．例题：

（1）有五个连续的偶数：

4、6、8、10、12，他们的平均数是多少？

（2）已知5个连续自然数的和是75，求这五个数分别是几？

5．模仿训练

（1）1＋2＋3＋…＋99＋100

（2）1＋3＋5＋7＋…＋99

（3）已知数列1、4、7、10、13……，298应该是其中的第几项？

（4）6＋10＋14＋…＋398＋402

（5）21＋23＋23＋…＋197＋199

（6）已知数列3、6、9、12、15……第51项是多少？

（7）丽丽学英语单词，第一天学会了6个，以后每天都比前一天多学会1个，那么第11天学会了学会了多少个单词？

（8）5个连续偶数的和是200，那么这10个数分别是多少？

（9）有一列数：

13、16、19、22、……307，这些数的平均数是多少？

第二讲：

速算与巧算

1．运算定律与性质：

（1）加减法运算定律：

a+b-c=a-c+b（a+b）+c=a+（b+c）a-b-c=a-（b+c）

（2）乘除法运算定律：

a×

b×

c=a×

（b×

c）a×

（b+c）=a×

b+a×

ca÷

b÷

c=a÷

c×

b

（a×

b）÷

b（a+b）÷

c+b÷

c

（3）去、添括号的性质：

-（），÷

（）去掉括号或添上括号要变号；

+（），×

（）去掉或添上括号不变号。

（4）利用商不变的性质使计算简单。

a+b-c=a-c+b

（1）843＋78-43

（2）843-86＋157

a-b-c=a-（b+c）；

去、添括号的性质

（1）528-（186＋328）

（2）564-（387-136）

c）；

a÷

c）

（1）25×

32×

125

（2）75000÷

125÷

8

5．例题：

（a×

b；

（1）56×

165÷

7÷

11

（2）44×

25

6．例题：

利用商不变的性质

（1）72×

53+72×

47

（2）2400÷

（1）329＋46-129

（2）647-86＋153

（3）528-186-314

（4）728-（347-172）

（5）25×

64×

125×

5

（6）3600÷

25÷

4

（7）8÷

7+9÷

7+11÷

7

（8）88×

（9）75×

27+19×

（10）9000÷

（11）20112011×

2010-2011×

20102010

第三讲：

错中求解

知识要点：

（1）和的变化规律：

如果一个加数不变，另一个加数增加（或减少）一个数，那么它们和也增加（或减少）同一个数。

（2）差的变化规律：

如果减数不变，被减数增加（或减少）一个数，那么它们的差也增加（或减少）同一个数。

如果被减数不变，减数增加（或减少）一个数，那么它们的差反而减少（或增加）同一个数。

（3）多加要减，少加再加；

多减要加，少减再减。

【多加要减，少加再加】

（1）小明在做一道加法时，把一个加数个位的2看作了4，另一个加数个位上的7看作9，结果计算的和为25，正确的和为多少？

（2）小华在计算两个数相加时，把第1个加数百位上的7错写成1，把第2个加数十位上的6错写成9，这样算得的和是443，正确的和应是多少？

【多减要加，少减再减】

（1）小马虎在做一道减法题时，把减数十位上的2看作5，结果得到的差是342，正确的差是多少？

（2）在减法算式中，错把减数百位上的5看成3，十位上的1看成7，结果得到的差是254，正确的差是多少？

（1）小马虎在做一道减法题时，把被减数百位上的6看成4，结果得到的差是212，正确的差是多少？

（2）小马虎在做减法题时，把被减数十位上的3写成8，个位上的2写成了5，结果得到的差是284，正确的差是多少？

（1）小马虎在做一道减法题时，把被减数十位上的4看成6，把减数十位上的2看作5，结果得到的差是52，正确的差是多少？

（2）小聪在计算一道减法题时，把被减数5023错写成5032，把减数千位上的3错写成2，十位上的5错写成8，这样得到的差是2352。

正确的差应是多少？

（1）小明在做一道加法时，把一个加数个位的5看作了8，另一个加数个位上的4看作6，结果计算的和为25，正确的和为多少？

（2）小华在计算两个数相加时，把第1个加数百位上的5错写成2，把第2个加数十位上的3错写成8，这样算得的和是444，正确的和应是多少？

（3）小马虎在做一道减法题时，把减数十位上的2看作5，结果得到的差是342，正确的差是多少？

（4）在减法算式中，错把减数百位上的6看成4，十位上的3看成8，结果得到的差是564，正确的差是多少？

（5）小马虎在做一道减法题时，把被减数百位上的8看成3，结果得到的差是212，正确的差是多少？

（6）小马虎在做减法题时，把被减数十位上的5写成8，个位上的4写成了7，结果得到的差是284，正确的差是多少？

（7）小马虎在做一道减法题时，把被减数十位上的3看成8，把减数十位上的4看作7，结果得到的差是252，正确的差是多少？

（8）小聪在计算一道减法题时，把被减数3046错写成3064，把减数千位上的2错写成1，十位上的4错写成7，这样得到的差是3360。

第四讲：

定义新运算

新运算，显然是与旧运算相对应，旧运算又是什么呢？

同学们可以思考一下，就运算就是学校里的四则运算“加减乘除”，对于这些运算，同学们应该很熟悉。

前面课程里，我们也讲到了很多旧的运算，今天我们要讲的就是新运算，既然是新运算，就是不同于以前的运算，为了不让同学们混淆了，所以就需要我们定义一下。

那么怎么样定义呢？

同学们可以与生活中结合起来，公共场所都有标志，这些标志都是我们人为定义的，新运算也是如此，关键点就是看如何定义的。

同时想提醒同学们注意，一个符号在一个问题里被定义了，不代表在所有题目里都是同一个意思，要结合题目的实际情况。

（1）设a、b都表示数，

规定：

a△b=a×

3－b×

2。

试计算：

（1）5△6；

（2）6△5。

（2）设a、b都表示数，

a○b=6×

a－2×

b。

试计算3○4

2．例题

（1）对于两个数a与b，规定a⊕b=a×

b＋a＋b，试计算6⊕2。

（2）对于两个数a与b，规定：

a⊕b=a×

b－（a＋b）。

计算3⊕5。

3．例题

（1）如果2△3=2＋3＋4，5△4=5＋6＋7＋8，按此规律计算3△5。

（2）如果5▽2=5×

6，2▽3=2×

3×

4，计算：

3▽3。

（1）对于两个数a与b，规定a□b=a（a+1）+（a+2）+…（a+b－1）。

已知x□6=27，求x

（2）如果2□3=2＋3＋4=9，6□5=6＋7＋8＋9＋10=40。

已知x□3=5973，求x

（1）设a、b都表示数，规定：

a*b=3×

a＋2×

（5*6）*7

（2）有两个整数是A、B，A▽B表示A与B的平均数。

已知A▽6=17，求A。

（3）对于两个数A与B，规定：

A☆B=A×

B÷

试算6☆4。

（4）对于两个数a与b，

a⊕b=a×

b＋a＋b。

如果5⊕x=29，求x。

（5）如果2▽4=24÷

（2＋4），3▽6=36÷

（3＋6），计算8▽4。

（6）如果2△3=2＋3＋4，5△4=5＋6＋7＋8，且1△x=15，求x。

（7）对于两个数a与b，规定a□b=a+（a+1）+（a+2）+…+（a+b－1），已知95□x=585，求x。

（8）如果1！

=1，2！

=1×

2=2，3！

2×

3=6，按此规律计算5！

。

第五讲：

平均数问题

我们经常用各科成绩的平均分数来比较班级之间，同学之间成绩的高低，求出各科成绩的平均数就是求平均数。

平均数在日常生活中和工作中应用很广泛，例如，求平均身高问题，求某天的平均气温等。

求平均数问题的基本数量关系是：

总数量÷

总份数=平均数

解答平均数问题的关键是要确定“总数量”以及与“总数量”相对应的“总份数”，然后用总数量除以总份数求出平均数。

1．例题1：

二

（1）班学生分三组植树，第一组有8人，共植树80棵；

第二组有6人，共植树66棵；

第三组有6人，共植树54棵。

平均每人植树多少棵？

2．例题2：

王老师为四年级羽毛球队的同学测量身高。

其中两个同学身高153厘米，一个同学身高152厘米，有两个同学身高149厘米，还有两个同学身高147厘米。

求四年级羽毛球队同学的平均身高。

3．例3：

从山顶到山脚的路长36千米，一辆汽车上山，需要4小时到达山顶，下山沿原路返回，只用2小时到达山脚。

求这辆汽车往返的平均速度。

4．例4：

李华参加体育达标测试，五项平均成绩是85分，如果投掷成绩不算在内，平均成绩是83分。

李华投掷得了多少他？

．

5．例5：

如果四个人的平均年龄是23岁，四个人中没有小于18岁的。

那么年龄最大的人可能是多少岁？

6．模仿训练

（1）电视机厂四月份前10天共生产电视机3300台，后20天共生产电视机6300台。

这个月平均每天生产电视机多少台？

（2）小明参加数学考试，前两次的平均分是85分，后三次的总分是270分。

求小明这五次考试的平均分数是多少。

（3）五

（1）班有7个同学参加数学竞赛，其中有两个同学得了99分，还有三个同学得了96分，另外两个同学分别得了97、89分。

这7个同学的平均成绩是多少？

（4）气象小组每天早上8点测得的一周气温如下：

13℃、13℃、13℃、14℃、15℃、14℃、16℃。

求一周的平均气温。

（5）小强家离学校有1200米，早上上学，他家到学校用了15分钟，从学校到家用了10分钟。

求小强往返的平均速度。

（6）李大伯上山采药，上山时他每分钟走50米，18分钟到达山顶；

下山时，他沿原路返回，每分钟