minitab实例分析PPT推荐.ppt
《minitab实例分析PPT推荐.ppt》由会员分享,可在线阅读,更多相关《minitab实例分析PPT推荐.ppt(71页珍藏版)》请在冰豆网上搜索。
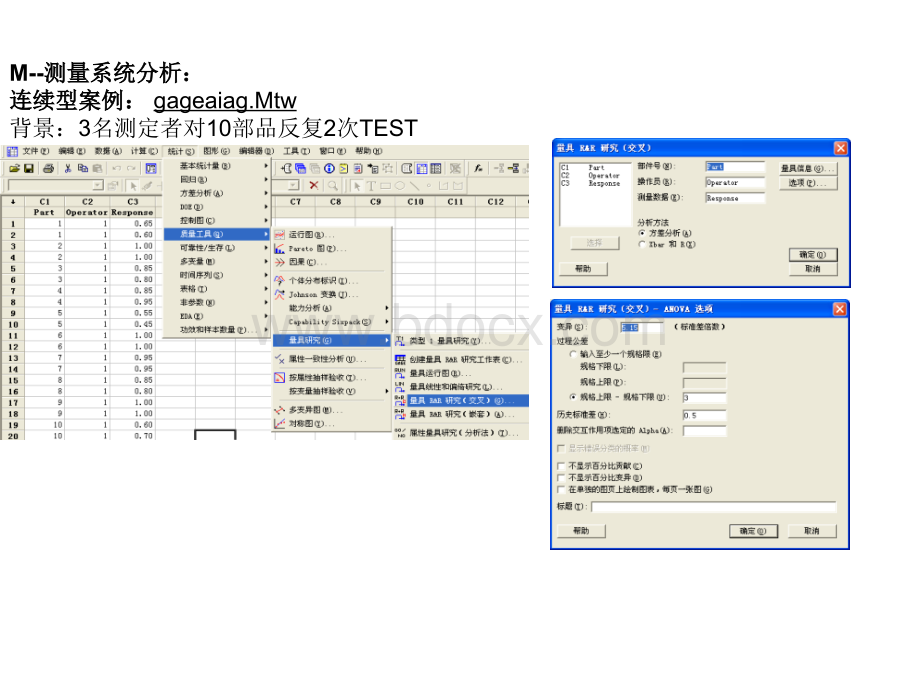
张一、张五需要追加训练;
(反复性)两数据不能相差较大,否则说明检查者一致的判定与标准有一定差异M-正态性测定正态性测定:
(测定工序能力的前提测定工序能力的前提)案例:
案例:
背景:
3名测定者对10部品反复2次TESTP-value0.05正态分布(P越大越好)本例:
P0.022,数据不服从正态分布。
原因:
1、Data分层混杂;
2、群间变动大;
M-工序能力分析(连续型):
工序能力分析(连续型):
Camshaft.MTW工程能力统计:
工程能力统计:
短期短期工序能力工序能力长期长期工序能力工序能力X平均目标值平均目标值CpCpmX平均平均目标值目标值CpCpm求解求解Zst(输入历史均值)(输入历史均值):
历史均值:
表示强行将它拉到中心位置不考虑偏移Zst(Bench)求解求解Zlt(无历史均值)(无历史均值):
无历史均值:
考虑偏移Zlt(Bench)*ZshiftZlt(Bench)Zlt(Bench)12.131.820.31工序能力分析:
工序能力分析:
Camshaft.MTW另:
另:
capabilitysixpack工具工具M-工序能力分析(离散型):
工序能力分析(离散型):
bpcapa.MTW
(1):
二项分布的:
二项分布的Zst缺陷率:
不良率是否受样本大小影响?
平均(预想)PPM226427Zlt0.75ZstZlt1.52.25M-工序能力分析(离散型):
bpcapa.MTW
(2):
Poisson分布的分布的ZstAGraph(坐标图):
(坐标图):
Pulse.MTW
(1)Histograpm(直方图)单变量(直方图)单变量通过形态确认:
正规分布有无;
异常点有无;
(2)Plot(散点图)(散点图)X、Y双变量双变量通过形态确认:
相关关系;
确认严重脱离倾向的点;
(3)MatrixPlot(行列散点图矩阵图)多变量(行列散点图矩阵图)多变量(4)BoxPlot(行列散点图矩阵图)多变量(行列散点图矩阵图)多变量(5)Multi-variChart(多变因图多变因图)Sinter.MTW目的:
掌握多X因子变化对Y的影响(大概);
材料和时间存在交互作用;
(5)Multi-variChart(多变因图多变因图)Sinter.MTW目的:
掌握多X因子变化对Y的影响();
倾斜越大,主效果越大无交互效果平行;
有交互效果交叉;
掌握多X因子变化对Y的影响(交互作用细节);
材料、交互的P有意;
A假设测定决定标本大小:
假设测定决定标本大小:
(1):
1-sampleZ(已知(已知u)背景:
HaN(30,100/25)H0N(25,100/n)为测定分布差异的标本大小有意水平=0.05查出力1=0.8差值:
u0ua2530-5功效值(查出力):
10.8标准差:
sigma10A假设测定决定标本大小:
(2):
1-sampleT(未知(未知u)背景:
10.8标准差(推定值)标准差(推定值):
sigma10样本数量27已知u的1-sampleZ的样本数量t分布假定母标准偏差未制定分析;
(3):
1Proportion(单样本)(单样本)背景:
H0:
P0.9Ha:
P0.9测定数据P10.8、P20.9有意水平=0.05查出力1=0.9P1=0.8功效值(查出力):
10.9P2=0.9母比率0.8实际上是否0.9以下,需要样本102个A假设测定决定标本大小:
2Proportion(单样本)(单样本)背景:
P1P2Ha:
P1P2有意水平=0.05查出力1=0.9P的备择值:
实际要测定的比例?
母比率;
功效值(查出力):
10.9假设P:
H0的P值(0.9)母比率0.8实际上是否小于0.9,需要样本217个A假设测定:
假设测定:
Camshaft.MTW
(1):
1-samplet(单样本)(单样本)背景:
对零件尺寸测定100次,数据能否说明与目标值(600)一致(=0.05)P-Value0.05Ho(信赖区间内目标值存在)可以说平均值为600A假设测定:
2sample-t.MTW
(2):
2-samplet(单样本)(单样本)背景:
判断两个母集团Data的平均,统计上是否相等(有差异)步骤:
分别测定2组data是否正规分布;
:
测定分散的同质性;
ttest;
正态性验证:
P-Value0.05正态分布P-Value0.05正态分布等分散测定:
等分散测定:
P-Value0.05等分散对Data的Box-plot标准偏差的信赖区间测定方法选择:
Ftest:
正态分布时;
Levensestest:
非正态分布时;
测定平均值:
P-Value0.05Hau1u2A假设测定:
Pairedt.MTW(3):
Pairedt(两集团从属(两集团从属/对应)对应)背景:
老化实验前后样本复原时间;
10样本前后实验数据,判断老化实验前后复原时间是否有差异;
(正态分布;
等分散;
=0.05)P-Value0.05Hau1u2(有差异)A假设测定:
(4):
1proportiont(离散单样本)(离散单样本)背景:
为确认某不良P是否为1,检查1000样本,检出13不良,能否说P=1%?
(=0.05)P-Value0.05H0P=0.01A假设测定:
2proportiont(离散单样本)(离散单样本)背景:
为确认两台设备不良率是否相等,A:
检查1000样本,检出14不良,B:
检查1200样本,检出13不良,能否说P1=P2?
(=0.05)P-Value0.05HoP1=P2A假设测定:
Chi-Square-1.MTW(5):
Chi-Squaret(离散单样本)(离散单样本)背景:
确认4个不同条件下,某不良是否有差异?
P-Value0.05HoP1=P2(无差异)应用一:
应用一:
测定频度数的同质性:
H0:
P1=P2=PnHa:
至少一个不等;
A假设测定:
Chi-Square-2.MTW(5):
确认班次别和不同类型不良率是否相关?
P-Value0.05Ha两因素从属(相关)应用二:
应用二:
测定边数的独立性:
独立的(无相关)独立的(无相关)Ha:
从属的(有相关);
班次班次不良类型不良类型AANOVA(分散分析):
(分散分析):
两个以上母集团的平均是否相等;
One-wayA(一因子多水平数)(一因子多水平数)背景:
确认三根弹簧弹力比较?
u1=u2=unHa:
P-Valueu无有意差;
1和2可以说无有意差,1和3有有意差;
AANOVA(分散分析):
Two-wayA(2因子多水平数)因子多水平数)背景:
确认生产线(因子1)、改善(因子2)影响下,测定值母平均是否相等,主效果和交互效果是否有意?
生产线:
P-Value0.05H0u相等,无差异;
信赖区间没有都重叠u有差别对结果有影响改善:
信赖区间重叠u无差别对结果没有影响A(相关分析):
(相关分析):
Scores.MTWP-Value确认哪个因子影响收率,利用2(5-1)配置法输入data:
表示25-1部分配置的清晰度和部分实施程度.曲线分析曲线分析:
-B、D、E有意;
-BD、DE有交互作用;
-在A=10,B=2,C=120,D=180,E=3时,Y95最佳;
统计性分析统计性分析:
实施t-test,判断有意因子B、D、E、BD、DE有意通过分散分析,判断1次效果、2次效果的有意性-主效果和交互作用效果都有意。
I最大倾斜法:
最大倾斜法:
一次试验一次试验
(1)因子配置设计因子配置设计:
反应值:
收率(Yield)时间35min,温度155时,Y80因子:
时间(30,40)温度(150,160)确认哪个因子影响收率,利用中心点包括的22配置法在中心点实验的次数!
一次试验一次试验
(2)统计性分析统计性分析:
实施对因子效果的t-test,判断有意的因子。
A,B有意;
通过分散分析判断1次效果、交互作用及曲率效果的有意性。
-1次效果(MainEffect)有意;
-弯曲不有意,故而没有曲率效果。
一次试验一次试验(3)确认最大倾斜方向确认最大倾斜方向:
线性变换的因子的水准还原为实际水准值。
-实际水平:
A(30,40),B(150,160)为还原实际水平值,线性变换的值各各乘5.利用追定的回归系数,决定最大倾斜方向()()最大倾斜方向:
A每增加1时,B增加0.42的方向。
StepCodedLevelUncodedLevel试验结果(收率)ABAB中心点003515580.4410.4252.181.08110.4240157.182.90220.8445159.283.14331.2650161.383.70441.6855163.484.33552.1060165.587.80662.5265167.688.65772.9470169.792.40883.3675171.893.54993.7880173.994.78101010104.204.208585176.0176.095.3095.3011114.6290178.194.2112125.0495180.292.51Step由实验者配置,Step10时Y取最大值,适用因子配置;
二次试验二次试验
(1)因子配置设计因子配置设计:
通过最大倾斜法求Y最大化的因子水平,通过追加实验,确认是否最佳水准的领域;
收率(Yield)时间(80,90)温度(171,181)确认哪个因子影响收率,利用中心点包括的22配置法二次试验二次试验
(2)统计性分析统计性分析:
对因子效果t-test,判断与Y有意因子-A,B有意-CtPtP64%,可以信赖回归模型;
通过分散分析,判断1、2次效果的有意性-1次效果、2次效果有意通过Lack-of-FitTest,判断模型的适合性-失拟0.05(不有意),因此判断模型适合(3)残差分析残差分析:
对残差的正态分布假说的研讨直方图、正态分布图对分散同质假说的研讨与拟合值残差已确定为随机分布,可以进行分散