17swsckyhhjc00302基础班闫华红财务全26讲Word文件下载.docx
《17swsckyhhjc00302基础班闫华红财务全26讲Word文件下载.docx》由会员分享,可在线阅读,更多相关《17swsckyhhjc00302基础班闫华红财务全26讲Word文件下载.docx(14页珍藏版)》请在冰豆网上搜索。
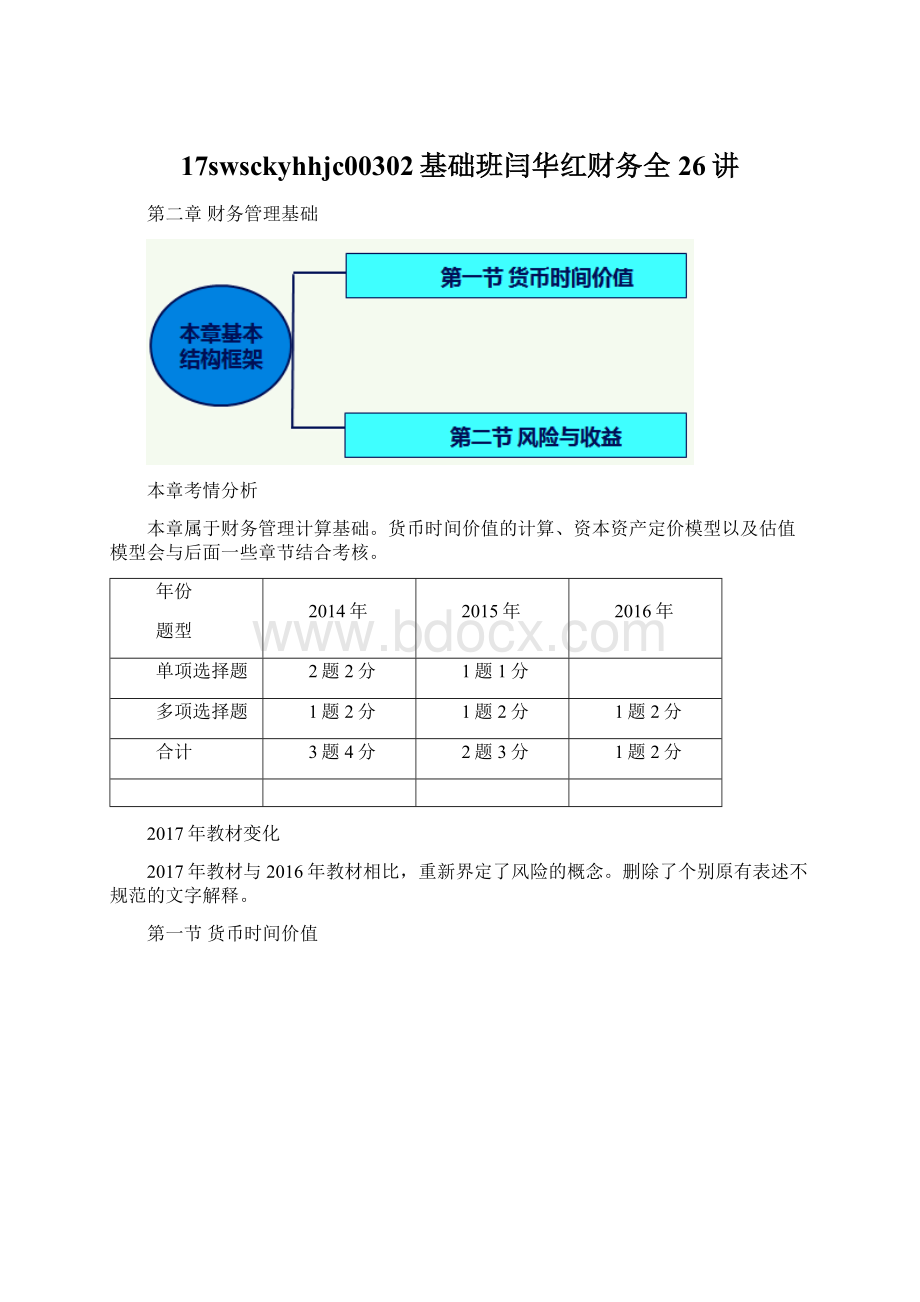
A.企业债券利率
B.社会平均利润率
C.通货膨胀率极低情况下的国债利率
D.无风险报酬率
【答案】C
【解析】应是无风险、无通货膨胀下的社会平均利润率。
二、终值和现值的计算
(一)利息的两种计算方法
单利计息:
只对本金计算利息,各期利息相等。
复利计息:
既对本金计算利息,也对前期的利息计算利息,各期利息不同。
(二)终值与现值的概念
终值又称将来值,是现在一定量的货币折算到未来某一时点所对应的金额,通常记作F。
现值,是指未来某一时点上一定量的货币折算到现在所对应的金额。
(三)一次性款项终值与现值
1.一次性款项终值
【教材例题2-1】某人将100元存入银行,复利年利率2%,求5年后的终值。
【答案】
F=P(1+i)n=100×
(l+2%)5=110.41(元)。
复利终值系数表
1元的复利终值系数,利率i,期数n,即(F/P,i,n)
期数
1%
2%
3%
4%
5%
6%
7%
1
1.0100
1.0200
1.0300
1.0400
1.0500
1.0600
1.0700
2
1.0201
1.0404
1.0609
1.0816
1.1025
1.1236
1.1449
3
1.0303
1.0612
1.0927
1.1249
1.1576
1.1910
1.2250
4
1.0406
1.0824
1.1255
1.1699
1.2155
1.2625
1.3108
5
1.0510
1.1041
1.1593
1.2167
1.2763
1.3382
1.4026
2.一次性款项现值
【教材例题2-2】某人为了5年后能从银行取出100元,在复利年利率2%的情况下,求当前应存入金额。
P=F/(1+i)n=100/(1+2%)5=90.57(元)。
复利现值系数表
1元的复利终值系数,利率i,期数为n的复利现值系数(P/F,i,n)
利率
0.9615
0.9524
0.9434
0.9346
0.9246
0.9070
0.8900
0.8734
0.8890
0.8638
0.8396
0.8163
0.8548
0.8227
0.7921
0.7629
0.8219
0.7835
0.7473
0.7130
计算题】某人拟购房,开发商提出两种方案,方案一是现在一次性付80万元,方案二是5年后付100万元,若目前的银行存款利率是7%,应如何付款?
(1)用终值比较:
方案一的终值:
F=800000×
(1+7%)5=1122080(元)
或F=800000×
(F/P,7%,5)=800000×
1.4026=1122080(元)
方案二的终值:
F=1000000
所以应选择方案二。
(2)用现值比较
方案二的现值:
P=1000000×
(1+7%)-5
或P=1000000×
(P/F,7%,5)=1000000×
0.713
=713000元<800000元
解答:
按现值比较,仍是方案二较好。
结论
(1)复利终值和复利现值互为逆运算;
(2)复利终值系数(1+i)n和复利现值系数1/(1+i)n互为倒数。
(四)年金
1.年金的含义
年金(annuity)是指间隔期相等的系列等额收付款
2.年金的种类
普通年金:
从第一期开始每期期末收款、付款的年金。
预付年金:
从第一期开始每期期初收款、付款的年金。
递延年金:
在第二期或第二期以后收付的年金。
永续年金:
无限期的普通年金。
3.普通年金的终值与现值
(1)普通年金终值
【教材例题2-3】小李是位热心公众事业的人,自2ⅹ07年12月底开始,他每年都要向一位失学儿童捐款。
小李向这位失学儿童每年捐款1000元,帮助这位失学儿童从小学一年级就读完九年义务教育。
假设每年定期存款利率都是2%,则小李9年的捐款在2ⅹ15年年底相当于多少钱?
F=A×
(F/A,2%,9)=1000×
9.7546=9754.6(元)。
(2)普通年金现值
【教材例题2-5】某投资项目于2ⅹ12年年初动工,假设当年投产,从投产之日起每年末可得收益40000元。
按年利率6%计算;
计算预期10年收益的现值。
P=40000×
(P/A,6%,10)
=40000×
7.3601=294404(元)。
计算题】举例10万元:
(1)某人存入10万元,若存款利率4%,第5年年末取出多少本利和?
(2)某人计划每年年末存入10万元,连续存5年,若存款利率4%,第5年年末账面的本利和为多少?
(3)某人希望未来第5年年末可以取出10万元的本利和,若存款利率4%,问现在应存入银行多少钱?
(4)某人希望未来5年,每年年末都可以取出10万元,若存款利率4%,问现在应存入银行多少钱?
(1)10×
(F/P,4%,5)=10×
1.2167=121670(元)
(2)10×
(F/A,4%,5)=10×
5.4163=541630(元)
(3)10×
(P/F,4%,5)=10×
0.8219=82190(元)
(4)10×
(P/A,4%,5)=10×
4.4518=445180(元)
复利终值系数表(F/P,i,n)
复利现值系数表(P/F,i,n)
年金终值系数表(F/A,i,n)
1.0000
2.0400
2.0500
2.0600
2.0700
3.1216
3.1525
3.1836
3.2149
4.2465
4.3101
4.3746
4.4399
5.4163
5.5256
5.6371
5.7507
年金现值系数表(P/A,i,n)
8%
0.9259
1.8861
1.8594
1.8334
1.8080
1.7833
2.7751
2.7232
2.6730
2.6243
2.5771
3.6299
3.5460
3.4651
3.3872
3.3121
4.4518
4.3295
4.2124
4.1002
3.9927
4.年偿债基金的计算
年偿债基金是指为了在约定的未来某一时点清偿某笔债务或积聚一定数额的资金而必须分次等额形成的存款准备金。
单选题】某人拟在5年后还清10000元债务,从现在起每年年末等额存入银行一笔款项。
假设银行利率为6%,则每年需存入款项为()。
[(P/A,6%,5)=4.2124,(F/A,6%,5)=5.6371]
A.1774
B.2374
C.5637
D.4212
【答案】A
【解析】
A=10000/(F/A,6%,5)
=10000/5.6371=1774(元)。
5.年资本回收额的计算
年资本回收额是指在约定年限内等额回收初始投人资本的金额。
单选题】假设以10%的利率借款20000元,投资于某个寿命为5年的项目,每年至少要收回多少现金才是有利的()。
[(F/P,10%,5)=1.6105,(P/F,10%,5)=0.6209,(P/A,10%,5)=3.7908,(F/A,10%,5)=6.1051]
A.33218
B.37908
C.5276
D.1638
A=20000/(P/A,10%,5)=20000/3.7908=5276(元)。
【结论】
①偿债基金与普通年金终值互为逆运算;
②偿债基金系数和普通年金终值系数的互为倒数;
③年资本回收额与普通年金现值互为逆运算;
④资本回收系数与普通年金现值系数互为倒数。
单选题】在利率和计算期相同的条件下,以下公式中,正确的是()。
A.普通年金终值系数×
普通年金现值系数=1
B.普通年金终值系数×
偿债基金系数=1
C.普通年金终值系数×
投资回收系数=1
D.普通年金终值系数×
预付年金现值系数=1
【答案】B
4.其他年金
(1)预付年金的终值与现值
方法1:
利用同期普通年金的公式乘以(1+i)
方法2:
利用期数、系数调整
预付年金终值和现值的计算公式
预付年金终值
=同期的普通年金终值×
(1+i)=A×
(F/A,i,n)×
(1+i)
=年金额×
预付年金终值系数=A×
[(F/A,i,n+1)-1]
预付年金现值
=同期的普通年金现值×
(P/A,i,n)×
预付年金现值系数=A×
[(P/A,i,n-1)+1]
【教材例题2-4】为给儿子上大学准备资金,王先生连续6年于每年年初存入银行3000元。
若银行存款利率为5%,则王先生在第6年年末能一次取出本利和多少钱?
[(F/A,I,n+1)-1]
=3000×
[(F/A,5%,7)-1]
(8.1420-1)=21426
或:
(F/A,I,n)×
F=3000×
(F/A,5%,6)×
(1+5%)
6.8019×
(1+5%)=21425.99
单选题】某公司打算购买一