届北师大版 用样本估计总体检测卷文档格式.docx

届北师大版 用样本估计总体检测卷文档格式.docx

《届北师大版 用样本估计总体检测卷文档格式.docx》由会员分享，可在线阅读，更多相关《届北师大版 用样本估计总体检测卷文档格式.docx（10页珍藏版）》请在冰豆网上搜索。

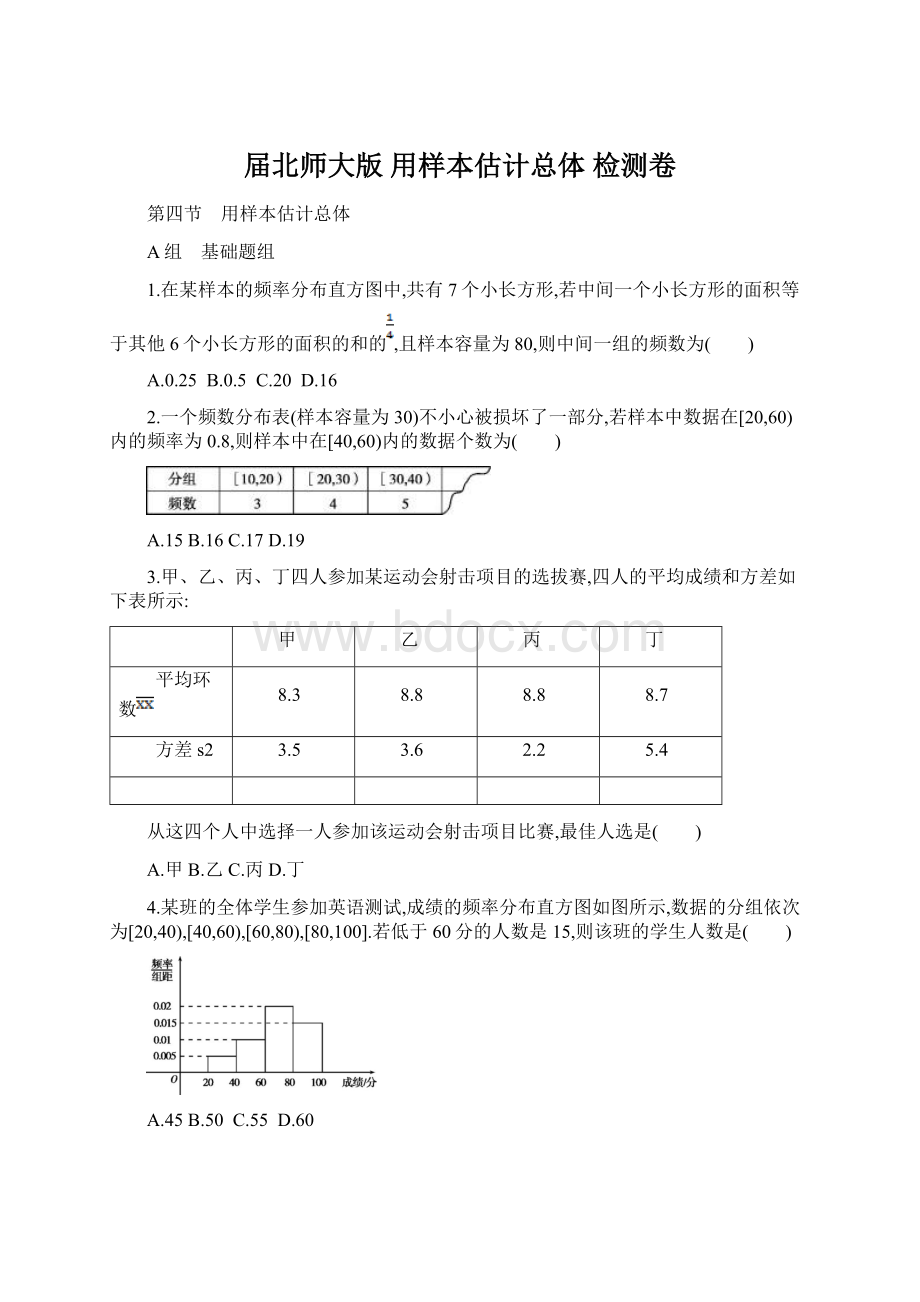
从这四个人中选择一人参加该运动会射击项目比赛,最佳人选是（　　）

A.甲B.乙C.丙D.丁

4.某班的全体学生参加英语测试,成绩的频率分布直方图如图所示,数据的分组依次为[20,40）,[40,60）,[60,80）,[80,100].若低于60分的人数是15,则该班的学生人数是（　　）

A.45B.50C.55D.60

5.某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5）,[5,10）,…,[30,35）,[35,40]时,所作的频率分布直方图是（　　）

6.已知样本数据x1,x2,…,xn的均值=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为　　　　. 

7.100名学生某次数学模块测试成绩（单位:

分）的频率分布直方图如图所示,则模块测试成绩落在[50,70）中的学生人数是　　　　. 

8.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:

学生

1号

2号

3号

4号

5号

甲班

6

7

8

乙班

9

若以上两组数据的方差中较小的一个为s2,则s2=　　　　. 

9.为检查某工厂所生产的8万台电风扇的质量,抽查了其中20台的无故障连续使用时限（单位:

小时）如下:

248　256　232　243　188　268　278　266　289　312

274　296　288　302　295　228　287　217　329　283

（1）完成下面的频率分布表,并作出频率分布直方图;

（2）估计8万台电风扇中有多少台无故障连续使用时限不低于280小时;

（3）用组中值（同一组中的数据在该组区间的中点值）估计样本的平均无故障连续使用时限.

分组

频数

频率

频率/组距

[180,200）

[200,220）

[220,240）

[240,260）

[260,280）

[280,300）

[300,320）

[320,340）

总计

0.05

10.随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从使用A、B两款订餐软件的商家中分别随机抽取50个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:

（1）试估计使用A款订餐软件的50个商家的“平均送达时间”的众数及平均数;

（2）根据以上抽样调查数据,将频率视为概率,回答下列问题:

（i）能否认为使用B款订餐软件的“平均送达时间”不超过40分钟的商家达到75%?

（ii）如果你要从A和B两款订餐软件中选择一款订餐,你会选择哪款?

说明理由.

B组　提升题组

11.（2016课标全国Ⅲ,4,5分）某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是（　　）

A.各月的平均最低气温都在0℃以上

B.七月的平均温差比一月的平均温差大

C.三月和十一月的平均最高气温基本相同

D.平均最高气温高于20℃的月份有5个

12.从甲、乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示（如图所示）.设甲、乙两组数据的平均数分别为、,中位数分别为m甲、m乙,则（　　）

甲

5

4

1

2

2

3

A.<

m甲>

m乙B.<

m甲<

m乙

C.>

m乙D.>

13.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则（　　）

A.甲的成绩的平均数小于乙的成绩的平均数

B.甲的成绩的中位数等于乙的成绩的中位数

C.甲的成绩的方差小于乙的成绩的方差

D.甲的成绩的极差小于乙的成绩的极差

14.如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35）,[35,40）,[40,45]的上网人数呈递减的等差数列分布,则年龄在[35,40）的网民出现的频率为（　　）

A.0.04B.0.06C.0.2D.0.3

15.（2014课标Ⅰ,18,12分）从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:

质量指标值分组

[75,85）

[85,95）

[95,105）

[105,115）

[115,125）

26

38

22

（1）作出这些数据的频率分布直方图;

（2）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）;

（3）根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?

答案全解全析

1.D　设中间一组的频数为x,

依题意有=,解得x=16.

2.A　由题意知,样本中在[40,60）内的数据个数为30×

0.8-4-5=15,故选A.

3.C　由题表中数据可知,丙的平均环数最高,且方差最小,说明技术稳定,且成绩好.故选C.

4.B　[20,40）内的频率为0.005×

20=0.1,[40,60）内的频率为0.01×

20=0.2,∴低于60分的频率为0.3,又低于60分的人数是15,∴该班学生的总人数为=50,故选B.

5.A　由题意可知,数据共被分为8组,所以选项C、D不符合,应排除;

由茎叶图知[0,5）的频数为1,==0.01,

[5,10）的频数为1,==0.01,

[10,15）的频数为4,==0.04,

……

由此可知,选项B不符合题意.故选A.

6.答案　11

解析　依题意有==5,则2x1+1,2x2+1,…,2xn+1的均值为=2+1=11.

7.答案　25

解析　由10（2a+3a+7a+6a+2a）=1,解得a=,故模块测试成绩落在[50,70）中的频率是10（2a+3a）=50a=50×

=,故对应的学生人数为100×

=25.

8.答案　

解析　由题表可得出乙班的数据波动性较大,则其方差较大,甲班的数据波动性较小,则其方差较小,易知甲班的数据的平均值为7,故方差s2=×

（1+0+0+1+0）=.

9.解析　

（1）频率分布表及频率分布直方图如下所示:

频率/组距

0.0025

0.10

0.0050

0.15

0.0075

0.20

0.0100

0.30

0.0150

20

1.00

（2）无故障连续使用时限不低于280小时的频率为0.30+0.10+0.05=0.45,故估计8万台电风扇中有8×

0.45=3.6（万台）无故障连续使用时限不低于280小时.

（3）由频率分布直方图可知

=190×

0.05+210×

0.05+230×

0.10+250×

0.15+270×

0.20+290×

0.30+310×

0.10+330×

0.05=269（小时）,所以估计样本的平均无故障连续使用时限为269小时.

10.解析　

（1）依题意可得,使用A款订餐软件的50个商家的“平均送达时间”的众数为55.

使用A款订餐软件的50个商家的“平均送达时间”的平均数为15×

0.06+25×

0.34+35×

0.12+45×

0.04+55×

0.4+65×

0.04=40.

（2）（i）使用B款订餐软件的“平均送达时间”不超过40分钟的商家的比例估计值为0.04+0.20+0.56=0.80=80%>

75%.

故可以认为使用B款订餐软件的“平均送达时间”不超过40分钟的商家达到75%.

（ii）使用B款订餐软件的50个商家的“平均送达时间”的平均数为15×

0.04+25×

0.2+35×

0.56+45×

0.14+55×

0.04+65×

0.02=35<

40,

所以选B款订餐软件.

11.D　由题中雷达图易知A、C正确.七月份平均最高气温超过20℃,平均最低气温约为13℃;

一月份平均最高气温约为6℃,平均最低气温约为2℃,所以七月的平均温差比一月平均温差大,故B正确.由题图知平均最高气温超过20℃的月份为六、七、八月,有3个.故选D.

12.B　由茎叶图知m甲==20,m乙==29,∴m甲<

m乙;

=×

（41+43+30+30+38+22+25+27+10+10+14+18+18+5+6+8）=,

（42+43+48+31+32+34+34+38+20+22+23+23+27+10+12+18）=,∴<

.

13.C　由题图知,甲的成绩为4,5,6,7,8,乙的成绩为5,5,5,6,9,所以甲、乙的成绩的平均数均为6,A错;

甲、乙的成绩的中位数分别为6、5,B错;

甲的成绩的方差=×

[（4-6）2+（5-6）2+（6-6）2+（7-6）2+（8-6）2]=2,乙的成绩的方差=×

[（5-6）2+（5-6）2+（5-6）2+（6-6）2+（9-6）2]=,<

C对;

甲、乙的成绩的极差均为4,D错.

14.C　由频率分布直方图可知,年龄在[20,25）的频率为0.01×

5=0.05,在[25,30）的频率为0.07×

5=0.35,又由题知,年龄在[30,35）,[35,40）,[40,45]的上网人数呈递减的等差数列分布,故其频率也呈递减的等差数列分布,则易知年龄在[35,40）的网民出现的频率为=0.2.故选C.

15.解析　

（1）

（2）质量指标值的样本平均数为

=80×

0.06+90×

0.26+100×

0.38+110×

0.22+120×

0.08=100.

质量指标值的样本方差为

s2=（-20）2×

0.06+（-10）2×

0.26+0×

0.38+102×

0.22+202×

0.08=104.

所以这种产品质量指标值的平均数的估计值为100,方差的估计值为1