高考数学统计概率超几何分布大题精做Word文档格式.docx
《高考数学统计概率超几何分布大题精做Word文档格式.docx》由会员分享,可在线阅读,更多相关《高考数学统计概率超几何分布大题精做Word文档格式.docx(8页珍藏版)》请在冰豆网上搜索。
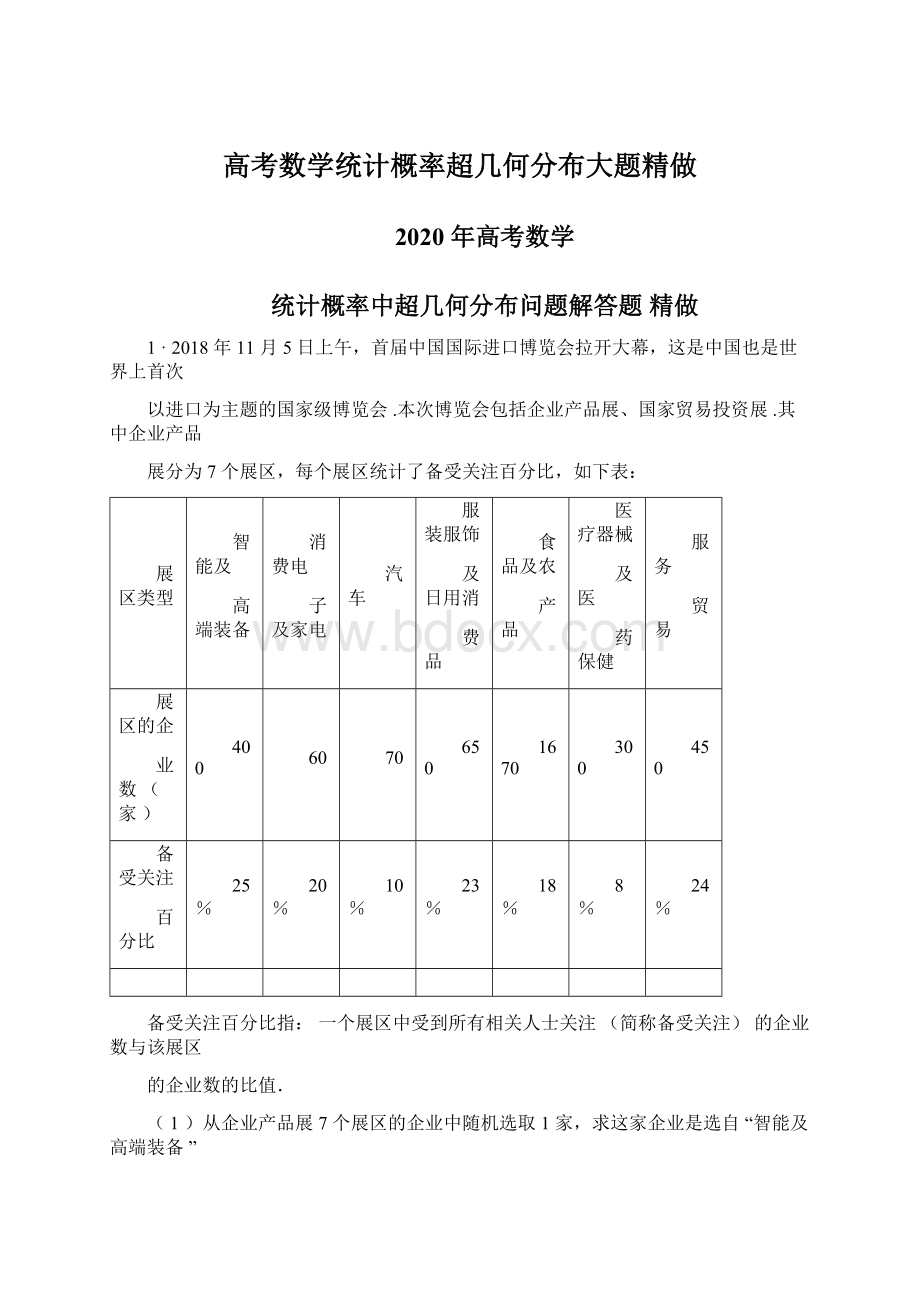
服务
贸易
展区的企
业数(家)
400
60
70
650
1670
300
450
备受关注
百分比
25%
20%
10%
23%
18%
8%
24%
备受关注百分比指:
一个展区中受到所有相关人士关注(简称备受关注)的企业数与该展区
的企业数的比值.
(1)从企业产品展7个展区的企业中随机选取1家,求这家企业是选自“智能及高端装备”
展区备受关注的企业的概率;
(2)从“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企
业中,任选2家接受记者采访.
(i)记X为这2家企业中来自于“消费电子及家电”展区的企业数,求随机变量X的分布列;
(ii)假设表格中7个展区的备受关注百分比均提升10%.记Y为这2家企业中来自于“消费
电子及家电”展区的企业数.试比较随机变量X,Y的均值EX和EY的大小.(只需写出结论)
2·
自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随
机抽取了100人,调查结果整理如下:
20以下
20,30
30,40
40,50
50,60
60,70
70以上
使用人数
3
12
17
6
4
2
未使用人数
14
36
(1)现随机抽取1名顾客,试估计该顾客年龄在30,50且未使用自由购的概率;
(2)从被抽取的年龄在50,70使用自由购的顾客中,随机抽取3人进一步了解情况,用X
表示这3人中年龄在50,60的人数,求随机变量X的分布列及数学期望;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该
超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
3.水果的价格会受到需求量和天气的影响.某采购员定期向某批发商购进某种水果,每箱
水果的价格会在当日市场价的基础上进行优惠,购买量越大优惠幅度越大,采购员通过对以
往的10组数据进行研究,发现可采用yaxb来作为价格的优惠部分y(单位:
元/箱)与购
买量x(单位:
箱)之间的回归方程,整理相关数据得到下表(表中Xilnxi,Yilnyi):
(1)根据参考数据,
①建立y关于x的回归方程;
②若当日该种水果的市场价为200元/箱,估算购买100箱该种水果所需的金额(精确到0.1
元).
(2)在样本中任取一点,若它在回归曲线上或上方,则称该点为高效点.已知这10个样本
点中,高效点有4个,现从这10个点中任取3个点,设取到高效点的个数为,求的数
学期望.
附:
对于一组数据x1,y1,x2,y2,,xn,yn,其回归直线y?
b?
xa?
的斜率和截距的最小
nxiyinxy
二乘估计分别为b?
i1,a?
yb?
x,参考数据:
e2.71828.
n22
i1xinx
4.为发挥体育在核心素养时代的独特育人价值,越来越多的中学已将某些体育项目纳入到
学生的必修课程,甚至关系到是否能拿到毕业证.某中学计划在高一年级开设游泳课程,为
了解学生对游泳的兴趣,某数学研究性学习小组随机从该校高一年级学生中抽取了100人进
行调查,其中男生60人,且抽取的男生中对游泳有兴趣的占5,而抽取的女生中有15人
表示对游泳没有兴趣.
(1)试完成下面的22列联表,并判断能否有99%的把握认为“对游泳是否有兴趣与性别
有关”?
有兴趣
没兴趣
合计
男生
女生
(2)已知在被抽取的女生中有6名高一
(1)班的学生,其中3名对游泳有兴趣,现在从这
6名学生中随机抽取3人,求至少有2人对游泳有兴趣的概率.
(3)该研究性学习小组在调查中发现,对游泳有兴趣的学生中有部分曾在市级和市级以上
游泳比赛中获奖,如下表所示.若从高一(8)班和高一(9)班获奖学生中各随机选取2
人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为,求随机变量的分布
列及数学期望.
班级
1
5
7
8
9
10
市级比赛
获奖人数
市级以上
比赛获奖
人数
PK2k0
0.500
0.400
0.250
0.150
0.100
0.050
0.025
[:
.]
0.010
0.005
0.001
k0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
2nadbc
K2
abcdacbd
A;
【答案】
(1)1;
(2)(i)见解析;
(ii)EXEY.
【解析】
(1)7个展区企业数共400607065016703004503600家,
其中备受关注的智能及高端装备企业共40025%100家,
设从各展区随机选1家企业,这家企业是备受关注的智能及高端装备为事件
X
46
16
11
P
105
35
ii)EXEY
1.【答案】
(1)17;
(2)详见解析;
(3)2200.
100
17人,
【解析】
(1)随机抽取的100名顾客中,年龄在30,50且未使用自由购的有314
2)X所有的可能取值为1,2,3,
X的分布列为
131
X的数学期望为EX1123312.
555
3)随机抽取的100名顾客中,使用自由购的有
3121764244人,
44
∴该超市当天至少应准备环保购物袋的个数估计为4450002200.
2.【答案】
(1)①yex2,②17281.7(元);
(2)6.
【解析】
(1)①对yaxb两边同时取自然对数得lnyblnxlna,
XiYi10XY1
令Xilnxi,Yilnyi,得YbXlna,∴b?
i101,lna1,∴ae,
10222
Xi210X22
i1
故所求回归方程为yex2.
20010e10017281.7(元).
2)由题意知可取0,1,2,3
3.【答案】
(1)见解析;
(2);
(3)见解析.
(1)由题得如下的列联表
无兴趣
50
25
15
40
总计
75
i0,1,2,3,
2)记事件Ai从这6名学生中随机抽取的3人中恰好有i人有兴趣,
则A2A3从这6名学生中随机抽取的3人中至少有2人有兴趣,且A2与A3互斥,
C2C1C3C0101
所求概率PPA2A3PA2PA33333,
C6C6202
24