立体几何提高教案Word下载.docx
《立体几何提高教案Word下载.docx》由会员分享,可在线阅读,更多相关《立体几何提高教案Word下载.docx(18页珍藏版)》请在冰豆网上搜索。
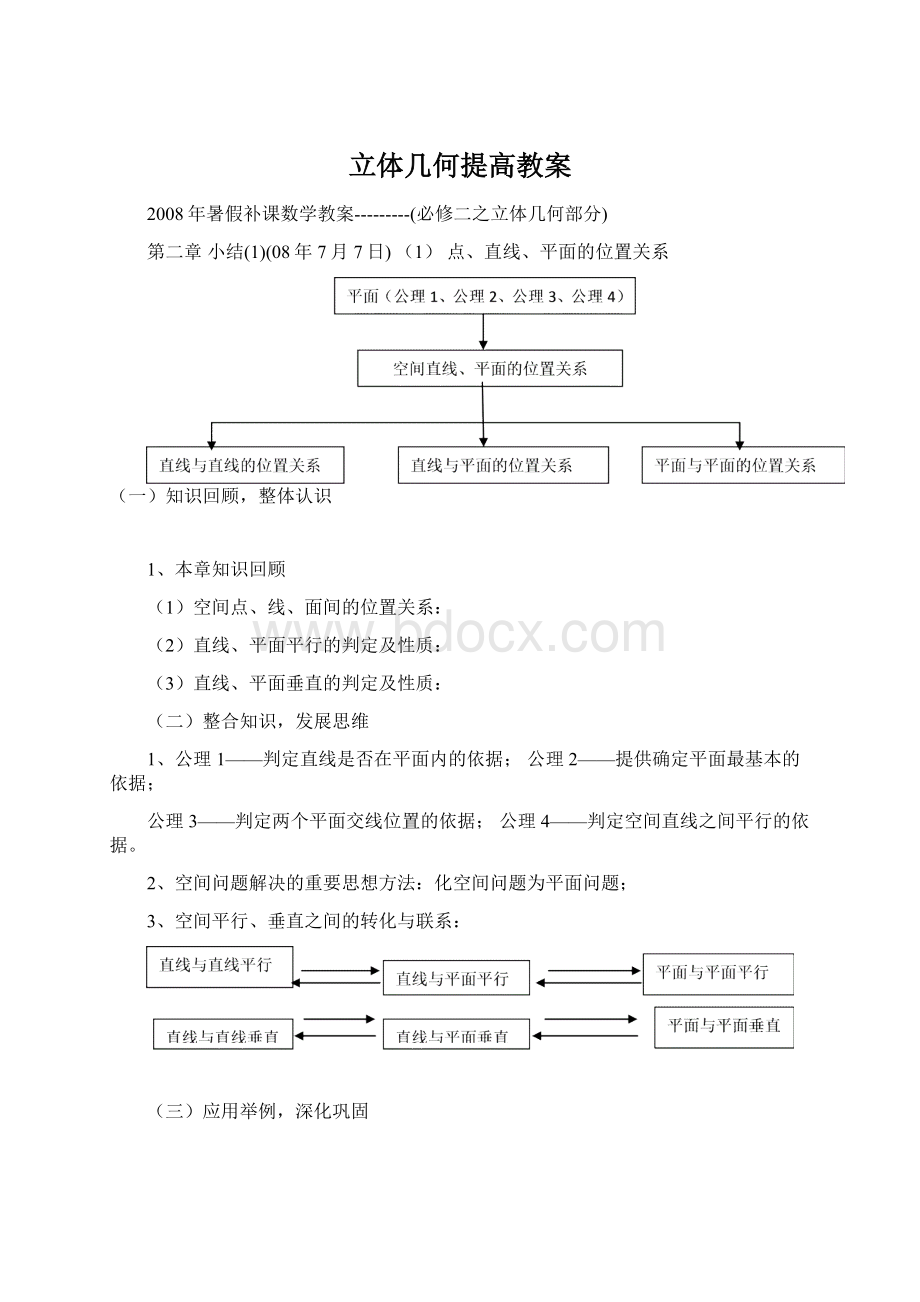
C.D.
2、设为两条直线,为两个平面,下列四个命题中,正确的命题是( D )
A.若与所成的角相等,则B.若,,则
C.若,则D.若,,则
3、如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
求证:
平面;
解:
证OE∥PB
4、如图,在正方体ABCD-A1B1C1D1中,求证:
面AB1D1∥面BDC1
通过两相交直线的平行可证明.
5.如图,在五面体中,点是矩形的对角线的交点,面是等边三角形,棱.
(1)证明//平面;
证FO∥EG
巩固训练:
A组题:
一、选择题:
1.有四个命题:
(1)、直线在平面内,直线在平面内,且相交,则平面与重合;
(2)、直线共面,直线相交,则直线共面。
(3)、直线在平面内,与平行,则与面没有公共点;
(4)、有三个公共点的两个平面一定重合;
以上命题中错误命题的个数是(C)
((A)1个(B)2个(C)3个(D)4个
2、已知,则等于(B)
ABCD以上几个都不对
3、如果直线直线b,且a//平面,那么b与的位置关系是(D)
A相交BCD
4、下列语句中,正确的个数为(A)
(1)一条直线和另一条直线平行,它和经过另一条直线的任何平面平行;
(2)一条直线和一个平面平行,它和这个平面内的任何直线平行;
(3)过平面外一点和这个平面平行的直线只有一条;
(4)平行于同一个平面的两条直线互相平行A0B1C2D3
5、如右图,ABCD--是正方体,分别为所在棱的中点,则下列结论正确的是(B)和为平行直线,和为相交直线
和为平行直线,和为相交直线
和为相交直线,和为异面直线
和为异面直线,和也是异面直线
二、填空题:
6、已知是两条异面直线,a上有三个点,b上有两个点,这些点可确定5个平面
7.不共线的三个平面两两相交,可将空间分成7或者8个部分.
8、在正方体的六个表面中,与异面组成角的对角线共有4条。
9、长方体ABCD--中,已知三条棱,,,则异面直线与所成的角的度数为60°
三、解答题:
10.已知在正方体中,E、F分别是的中点,求证:
平面平面
11、已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点,
AM面EFG
12、如图,四边形ABCD是矩形,面ABCD,过BC作平面BCFE交AP于E,
交DP于F,求证:
四边形BCFE是梯形
B组题:
四、选择题:
13.A,b是异面直线,A,B是a上的两点,C,D是b上的两点,M,N分别是线段AC,BD的中点,则MN和a的位置关系为(A)
A异面B平行C相交D以上三种关系都有可能
14.如图所示,在正方体中,M为AB的中点,则异面直线与CM所成角的余弦值为(D)(A)(B)C(D)
15、已知直线与直线垂直,平行于平面,则与平面的位置关系是(D)
A.B.C.与平面相交D.以上都有可能
16、是空间四边形,分别是四条边的任意四点,则下列结论正确的是(D)A.和是相交直线B.EH和FG是平行直线
C.和是异面直线D.以上情况都有可能
17、正方体中,、、分别是、、的中点.那么正方体的过、、的截面图形是(D)
A.三角形B.四边形C.五边形D.六边形
五、填空题:
18.三个平面将空间最少分成部分,最多分成部分,则等于12.
19.三条直线中有两条平行,第三条和这两条都相交时确定1个平面;
三条直线交于一点时可确定__1或者3个平面;
三条直线互相平行时,最多可确定3个平面。
20.连接抛物线上任意四点组成的四边形可能是②③⑤(填写所有正确选项的序号)①菱形②有3条边相等的四边形③梯形④平行四边形⑤有一组对角相等的四边形
21.已知m、n是不同的直线,是不重合的平面,给出下列命题:
①若则②若则③m、n是两条异面直线,若则上面命题中,真命题的序号是_____③_______(写出所有真命题的序号)
六、解答题:
22.正方体ABCD—A1B1C1D1的棱长为
(1)、求△AB1D1的面积;
(2)、求三棱锥的体积。
解、①②
23.已知直四棱柱中,,底面是直角梯形,,,,,,求异面直线与所成的角的余弦值(解:
为)
24、过正方体的棱作一平面交平面于,求证:
//
第二章小结
(2)(08年7月8日)
1.直线和平面垂直的判定及性质;
2.平面和平面垂直的判定及性质.
(二)应用举例,深化巩固
1、如图,在三棱锥V-ABC中,VA=VC,AB=BC,求证:
VB⊥AC.
2、过△ABC所在平面外一点P,作PO⊥,垂足为O,连接PA,PB,PC.
(1)若PA=PB=PC,∠C=90°
,则点O是AB边的中点.
(2)若PA=PB=PC,则点O是△ABC的外心.
(3)若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的垂心.
3、如图,已知空间四边形ABCD的边BC=AC,AD=BD,引BE⊥CD,E为垂足,作AH⊥BE于H.求证:
AH⊥平面BCD.
4.已知ABCD是正方形,PA⊥平面ABCD,BE⊥PC,E为垂足.
平面BDE⊥平面PBC.
PC⊥面BDE
训练提高练习:
C组题:
七、选择或填空题:
25、平面平面,平面平面,平面平面,若,
则与的位置关系是(D)
A.与异面B.与相交C.至少与中的一条相交D.与都平行
26.平面过直线外的两点,若要这个平面与平行,则这样的平面有(D)
A无数个B一个C不存在D上述情况都有可能
八、解答题:
27.如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1求BF的长;
(2注意到AE∥FC1)
28.两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:
MN∥平面BCE。
29.(08高考宁夏18)(本小题满分12分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的正视图和侧视图在下面画出(单位:
cm)(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连结,证明:
面.
俯视图为:
第二章小结(3)(08年7月9日)
1.异面直线所成角;
2.直线与平面所成角;
3.两平面所成角.
例1.已知空间四边形ABCD中,P、Q分别是AB、CD的中点,且PQ=3,AC=4,BD=2,AC与BD所成角的大小.
例2.已知四面体ABCD的各棱长均相等,E、F分别为AB、CD的中点,求EF与AC所成角的大小.
例3.在四面体ABCD中,平面ABD⊥平面BCD,△ABD为等边三角形,CD⊥BD,∠DBC=30o.
(1)求二面角A-DC-B的大小;
(2)求二面角A-BC-D的平面角的正切值;
(3)求二面角D-AB-C的平面角的正切值.
注意三垂线法的应用与讲解.
例4.圆台上、下底面半径分别为2、4,O1A1、OB分别为上、下底面的半径,二面角A1-OO1-B是60o,圆台母线与底面成60o角.
(1)求A1B和OO1所成角的正切值;
(2)求圆台的侧面积及体积.
解;
注意概念的转化,实为一个三棱台的问题.
例5.在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90o,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点,求CD与平面ADMN所成角的正弦.
注意到BN⊥面ADMN
第二章小结(4)——空间距离(08年7月10日)
一、复习目的:
1.掌握两条直线所成的角和距离的概念及等角定理;
(对于异面直线的距离,只要求会计算已给出公垂线时的距离)。
2.掌握点、直线到平面的距离,直线和平面所成的角;
3.掌握平行平面间的距离,会求二面角及其平面角;
二、教学过程
1.基本知识:
(1)空间中的距离是立体几何的重要内容,其内容主要包括:
点点距,点线距,点面距,线线距,线面距,面面距。
其中重点是点点距、点线距、点面距以及两异面直线间的距离.因此,掌握点、线、面之间距离的概念,理解距离的垂直性和最近性,理解距离都指相应线段的长度,懂得几种距离之间的转化关系,所有这些都是十分重要的。
(2)求距离的重点在点到平面的距离,直线到平面的距离和两个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可以转化成另外一个点到这个平面的距离。
(3)点到平面的距离
平面外一点P在该平面上的射影为P′,则线段PP′的长度就是点到平面的距离;
求法:
“一找二证三求”,三步都必须要清楚地写出来。
等体积法。
(4)直线与平面的距离:
一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;
(5)平行平面间的距离:
两个平行平面的公垂线段的长度,叫做两个平行平面的距离。
求距离的一般方法和步骤:
应用各种距离之间的转化关系和“平行移动”的思想方法,把所求的距离转化为点点距、点线距或点面距求之,其一般步骤是:
①找出或作出表示有关距离的线段;
②证明它符合定义;
③归到解某个三角形.若表示距离的线段不容易找出或作出,可用体积等积法计算求之。
2、举例分析
例1、正方形ABCD的边长是2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图所示).M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCFE所成角的正切值为,那么点M到直线EF的距离为。
例2.如图,四面体ABCD中,O、E分别BD、BC的中点,CA=CB=CD=BD=2。
△ABD为等腰直角三角形。
(Ⅰ)求证:
AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离。
注意平移之后再求距离的问题的应用.
★【例题3】、如图,四棱锥的底面为菱形,且,,的中点.
(1)求直线与平面所成角的大小;
(2)求二面角的平面角的正切值;
(3)在线段上是否存在一点,使成立?
如果存在,求出的长;
如果不存在,请说明理由.
本题最好使用几何法加以处理.
★【例题4】、如图,直平行六面体ABCD-A′B′C′D′的底面ABCD是边长为2的菱形,∠BAD=60°
E为AB的中点,二面角A′-ED-A为60°
;
(1)、求证:
平面A′ED⊥平面ABB′A′;
(2)、求二面角A′-ED-C′的大小;
(3)、求点C′到平面A′ED的距离。
本题第一问最好用几何法处理,第