河南郑州市高三第二次模拟文科数学试题及答案Word文件下载.docx

河南郑州市高三第二次模拟文科数学试题及答案Word文件下载.docx

《河南郑州市高三第二次模拟文科数学试题及答案Word文件下载.docx》由会员分享，可在线阅读，更多相关《河南郑州市高三第二次模拟文科数学试题及答案Word文件下载.docx（8页珍藏版）》请在冰豆网上搜索。

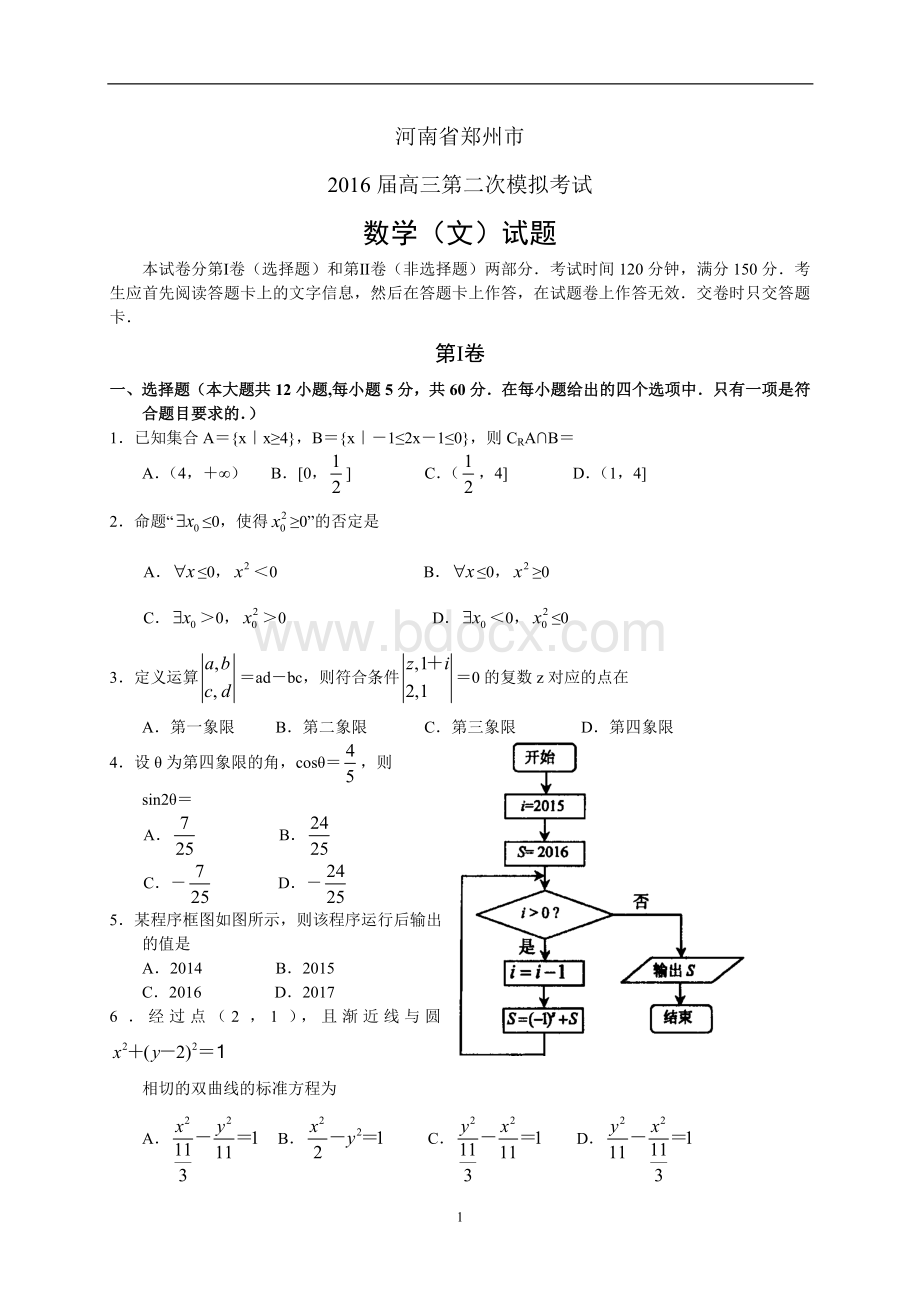
6．经过点（2，1），且渐近线与圆

相切的双曲线的标准方程为

A．B．C．D．

7．平面内满足约束条件，的点（x，y）形成的区域为M，区域M关于直线2x

＋y＝0的对称区域为，则区域M和区域内最近的两点的距离为

A．B．C．D．

8．将函数f（x）＝－cos2x的图象向右平移个单位后得到函数g（x），则g（x）具有性质

A．最大值为1，图象关于直线x＝对称

B．在（0，）上单调递减，为奇函数

C．在（，）上单调递增，为偶函数

D．周期为π，图象关于点（，0）对称

9．如图是正三棱锥V－ABC的正视图、侧视图和

俯视图，则其侧视图的面积是

A．4B．5

C．6D．7

10．已知定义在R上的奇函数y＝f（x）的图像关于直线x＝1对称，当0＜x≤1时，f（x）

＝，则方程f（x）－1＝0在（0，6）内的零点之和为

A．8B．10C．12D．16

11．设数列{}满足：

a1＝1，a2＝3，且2n＝（n－1）＋（n＋1），则a20的值

是

A．4B．4C．4D．4

12．对∈R，n∈[0，2]，向量c＝（2n＋3cosα，n－3sinα）的长度不超过6的概率为

A．B．C．D．

第Ⅱ卷

本卷包括必考题和选考题两部分．第13—21题为必考题,每个试题考生都必须作答．第22－24题为选考题．考生根据要求作答．

二、填空题（本大题共4小题，每小题5分，共20分．）

13．曲线f（x）＝－x＋3在点P（1，3）处的切线方程是_________．

14．已知{}为等差数列，公差为1，且a5是a3与a11的等比中项，则a1＝_________．

15．已知正数x，y满足＋2xy－3＝0，则2x＋y的最小值是___________．

16．在正三棱锥V—ABC内，有一半球，其底面与正三棱锥的底面重合，且与正三棱锥的三个侧面都相切，若半球的半径为2，则正三棱锥的体积最小时，其高等于__________．

三、解答题（解答应写出文字说明，证明过程或演算步骤）

17．（本小题满分12分）

在△ABC中，角A、B、C所对的边分别为a、b、c，且满足cos2C－cos2A＝2sin（＋

C）·

sin（－C）．

（Ⅰ）求角A的值；

（Ⅱ）若a＝且b≥a，求2b－c的取值范围．

18．（本小题满分12分）

为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机抽调了50人，他们年龄的频数分布及支持“生育二胎”人数如下表：

（Ⅰ）由以上统计数据填下面2乘2列联表，并问是否有99％的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异；

（Ⅱ）若对年龄在[5，15）的被调查人中各随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少?

参考数据：

19．（本小题满分12分）

如图，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，

∠BCD＝120°

，四边形BFED为矩形，平面BFED⊥

平面ABCD，BF＝1．

（Ⅰ）求证：

AD⊥平面BFED；

（Ⅱ）已知点P在线段EF上，＝2．求三棱锥E－APD

的体积．

20．（本小题满分12分）

已知曲线C的方程是（m＞0，n＞0），且曲线C过A（，），B（，

）两点，O为坐标原点．

（Ⅰ）求曲线C的方程；

（Ⅱ）设M（x1，y1），N（x2，y2）是曲线C上两点，向量p＝（x1，y1），q＝（x2，y2），且p·

q＝0，若直线MN过（0，），求直线MN的斜率．

21．（本小题满分12分）

已知函数f（x）＝．

（Ⅰ）讨论函数y＝f（x）在x∈（m，＋∞）上的单调性；

（Ⅱ）若m∈（0，]，则当x∈[m，m＋1]时，函数y＝f（x）的图象是否总在函数

g（x）＝＋x图象上方?

请写出判断过程．

请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分，做答时，用2B铅笔在答题卡上把所选题目对应的题号涂黑．

22．（本小题满分10分）选修4—1：

几何证明选讲

如图，正方形ABCD边长为2，以A为圆心、DA为半径的

圆弧与以BC为直径的半圆O交于点F，连结BF并延长交

CD于点E．

E为CD的中点；

（Ⅱ）求EF·

FB的值．

23．（本小题满分10分）选修4—4：

坐标系与参数方程

平面直角坐标系xOy中，曲线C：

．直线l经过点P（m，0），且倾斜角为．以O为极点，以x轴正半轴为极轴，建立极坐标系．

（Ⅰ）写出曲线C的极坐标方程与直线l的参数方程；

（Ⅱ）若直线l与曲线C相交于A，B两点，且｜PA｜·

｜PB｜＝1，求实数m的值．

24．（本小题满分10分）选修4—5：

不等式选讲

已知函数f（x）＝｜x＋6｜－｜m－x｜（m∈R）．

（Ⅰ）当m＝3时，求不等式f（x）≥5的解集；

（Ⅱ）若不等式f（x）≤7对任意实数x恒成立，求m的取值范围．

参考答案

一、选择题

BAADDADBCCDC

二、填空题

13.，14.，15.，16.

三、解答题（解答应写出文字说明。

证明过程或演算步骤）

17．解：

（1）由已知得，………2分

化简得，故．………………………………5分

（2）由正弦定理，得，…7分

因为，所以，，………9分

故=

……………………………11分

所以．………12分

18．解：

（Ⅰ）2乘2列联表

年龄不低于45岁的人数

年龄低于45岁的人数

合计

支持

32

不支持

18

合计

10

40

50

……………………………2分

＜………………4分

所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.

………………5分

（Ⅱ）设年龄在[5,15）中支持“生育二胎”的4人分别为a,b,c,d,不支持“生育二胎”的人记为M,………………6分

则从年龄在[5,15）的被调查人中随机选取两人所有可能的结果有：

（a,b）,（a,c）,（a,d）,（a,M）,（b,c）,（b,d）,（b,M）,（c,d）,（c,M）,（d,M）.…………8分

设“恰好这两人都支持“生育二胎””为事件A，………………9分

则事件A所有可能的结果有：

（a,b）,（a,c）,（a,d）,（b,c）,（b,d）,（c,d）,

∴………………11分

所以对年龄在[5,15）的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为.………………12分

19．解：

（1）在梯形中，

∵∥，

∴∴…………………2分

∴∴∵平面平面

平面平面，

∴…………………4分

∴又∴…………………6分

（2）由

（1）知⊥平面…………………8分

∵//,∴且…………………10分

∴…………………12分

20.解：

（1）由题可得：

，解得

所以曲线方程为........4分

（2）设直线的方程为，代入椭圆方程为得：

∴，…………6分

∴=…………8分

∴…………10分

即................12分

21.（本小题满分12分）

解：

（1）

，，

所以.…………4分

（2）由

（1）知所以其最小值为.

因为，在最大值为…………6分

所以下面判断与的大小，即判断与的大小，其中

令，，令，则

因所以，单调递增；

…………8分

所以，故存在

使得

所以在上单调递减，在单调递增…………10分

所以

所以时，

即也即

所以函数的图象总在函数图象上方．……………..12分

22．解：

（Ⅰ）由题可知是以为圆心，为半径作圆，而为正方形，

∴为圆的切线.

依据切割线定理得.………………………………2分

∵圆以为直径，∴是圆的切线，

同样依据切割线定理得.……………………………4分

故.

∴为的中点.……………………………5分

（Ⅱ）连结，∵为圆的直径，

∴………………………………6分

由

得…………………………8分

又在中，由射影定理得……………………10分

23．解：

（1）即,

.…………2分

…………5分

（2）

…………8分

…………10分

24．解：

（1）当时，即，

①当时，得，所以；

②当时，得，即，所以；

③当时，得，成立，所以.…………………………………4分

故不等式的解集为.…………………………………5分

（Ⅱ）因为＝

由题意得，则，…………8分

解得,

故的取值范围是.……………………………………………10分

8