高考数学立体几何变式题练习docWord文件下载.docx

高考数学立体几何变式题练习docWord文件下载.docx

《高考数学立体几何变式题练习docWord文件下载.docx》由会员分享，可在线阅读，更多相关《高考数学立体几何变式题练习docWord文件下载.docx（12页珍藏版）》请在冰豆网上搜索。

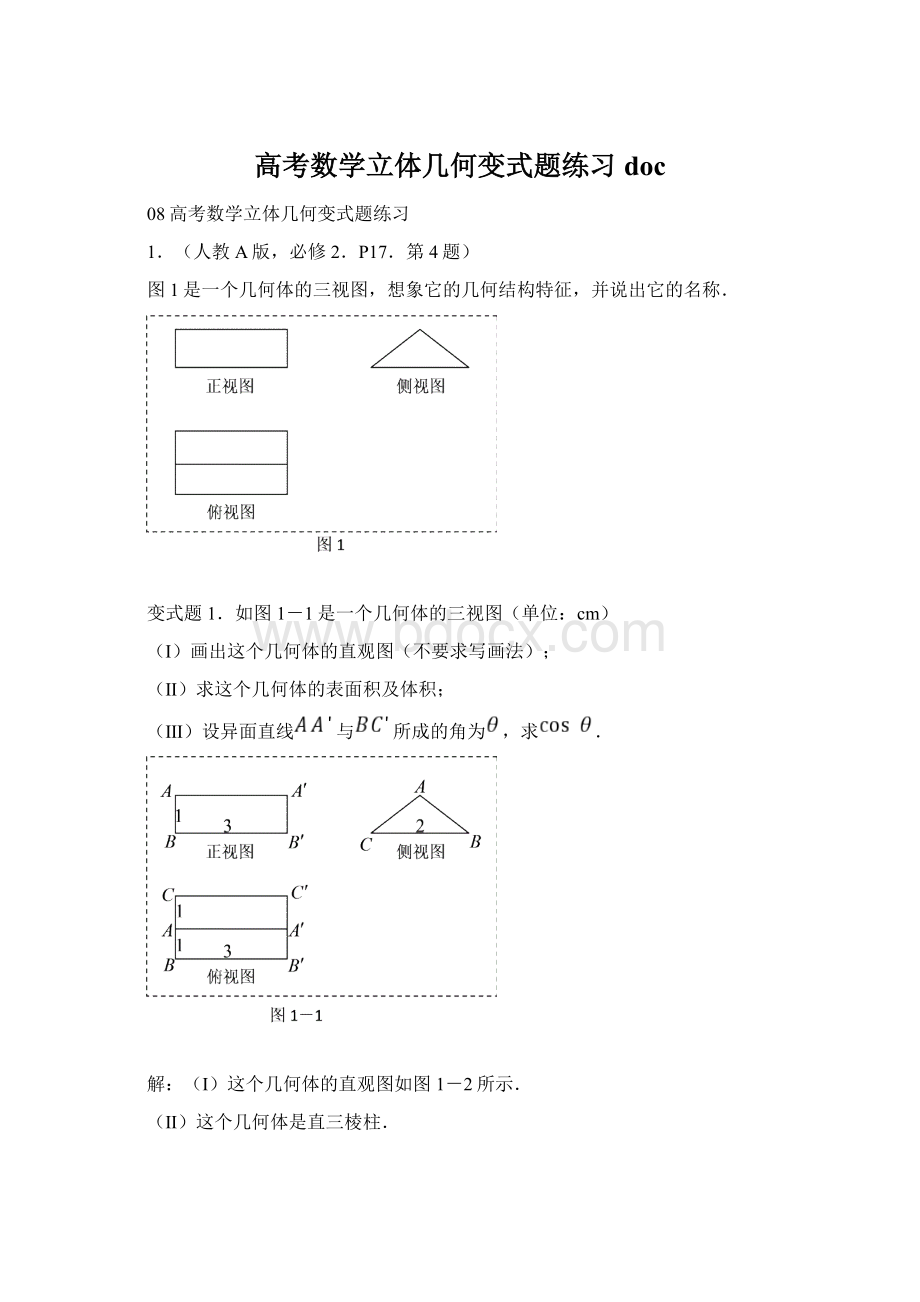
由于底面的高为1，所以．

故所求全面积

　　　　　　．

这个几何体的体积

（Ⅲ）因为，所以与所成的角是．

　　　在中，，

　　　故．

2．（人教A版，必修2，P20．例3）

如图2，已知几何体的三视图，用斜二测画法画出它的直观图．

变式题2－1．如图2－1．已知几何体的三视图（单位：

cm）．

（Ⅰ）画出它的直观图（不要求写画法）；

（Ⅱ）求这个几何体的表面积和体积．

解（Ⅰ）这个几何体的直观图如图2－2所示．

（Ⅱ）这个几何体是一个简单组合体，它的下部是一个圆柱（底面半径为1cm，高为2cm），它的上部是一个圆锥（底面半径为1cm，母线长为2cm，高为cm）．

所以所求表面积，

所求体积．

变式题2－2．如图2－3，已知几何体的三视图（单位：

（Ⅲ）设异面直线、所成角为，求．（理科考生）

（Ⅰ）这个几何体的直观图如图2－4所示．　

（Ⅱ）这个几何体可看成是由正方体及直三棱柱的组合体．

由，，

可得．

故所求几何体的全面积

所求几何体的体积

（Ⅲ）由，且，可知，

故为异面直线、所成的角（或其补角）．

由题设知，，

取中点，则，且，

．

由余弦定理，得

　　　　　　　　　　　　　　　　．

3．（北师大版．必修2．P31．第4题）

如图3，已知E，F分别是正方体的棱和棱上的点，且，求证：

四边形是平行四边形

变式题：

如图3－1．已知、分别是正方体的棱和棱的中点．

（Ⅰ）试判断四边形的形状；

（Ⅱ）求证：

平面平面．

解（Ⅰ）如图3－2，取的中点，连结、．

∵、分别是和的中点，

∴，

在正方体中，有

，　∴，

∴四边形是平行四边形，

∴．

又、分别是、的中点，

∴四边形为平行四边形，

故．

∴四边形是平行四边形．

又≌，

故四边形为菱形．

（Ⅱ）连结、、．∵四边形为菱形，

，

∴平面．

又平面，

又，

故平面平面

4．（人教A版，必修2，P74．例2）

如图4，在正方体中，求直线与平面所成的角．

如图4－1，已知正四棱柱中，底面边长，侧棱的长为4，过点作的的垂线交侧棱于点，交于点．

（Ⅰ）求证：

平面；

（Ⅱ）求与平面所成的角的正弦值．

（Ⅰ）如图4－2，以为原点，、、所在直线分别为、、轴建立空间直角坐标系．

设，则．

∵，∴．

∴，∴，．

∴且．

∴且．∴平面．

（Ⅱ）由（Ⅰ）知是平面的一个法向量，又，

∴与平面所成角的正弦值为．

5．（人教A版，必修2，P87，第10题）

如图5，已知平面，且是垂足，试判断直线与的位置关系？

并证明你的结论．

变式题5－1，如图5，已知平面，且是垂足．

（Ⅱ）若，试判断平面与平面的位置关系，并证明你的结论．

变式题5－1，如图5，已知平面，

且是垂足．

解（Ⅰ）因为，所以．同理．

又，故平面．

（Ⅱ）设与平面的交点为，连结、．

因为平面，所以，

所以是二面角的平面角．

又，所以，即．

在平面四边形中，，

所以．

故平面平面．

变式题5－2．如图5－1，已知直二面角，与平面、所成的角都为，．

为垂足，为垂足．

（Ⅰ）求直线与所成角的大小；

（Ⅱ）求四面体的体积．

（Ⅰ）如图5－2，在平面内，作，连结、．则四边形为平行四边形，所以，即为直线与所成的角（或其补角）．

因为．

所以．同理．

又与平面、所成角为，所以，，所以，．

在中，，从而．

因为，且为平行四边形，

又，所以．

故平面，从而．

在中，．

所以，

即直线与所成角的大小为．

（Ⅱ）在中，，所以．

三角形的面积，

故四面体的体积

6．（人教A版，必修2，P87，B组第1题）

如图5，边长为2的正方形ABCD中，

（1）点是的中点，点是的中点，将分别沿折起，使两点重合于点，求证：

（2）当时，求三棱锥的体积．

变式题．如图5－1，在矩形中，是的中点，以为折痕将向上折起，使为，且平面平面．

；

（Ⅱ）求直线与平面所成角的正弦值．

解（Ⅰ）在中，，

在中，，

∵，

∵平面平面，且交线为，

∵平面，

（Ⅱ）设与相交于点，由（Ⅰ）知，

∴平面，

∴平面平面，且交线为，

如图6－2，作，垂足为，则平面，

连结，则是直线与平面所成的角．

由平面几何的知识可知，∴．

在中，，可求得．

∴直线与平面所成的角的正弦值为．