安徽中考数学模拟试题及答案文档格式.docx
《安徽中考数学模拟试题及答案文档格式.docx》由会员分享,可在线阅读,更多相关《安徽中考数学模拟试题及答案文档格式.docx(9页珍藏版)》请在冰豆网上搜索。
5.分式方程的解是【】
A.x=1B.x=-1C.x=2D.x=-2
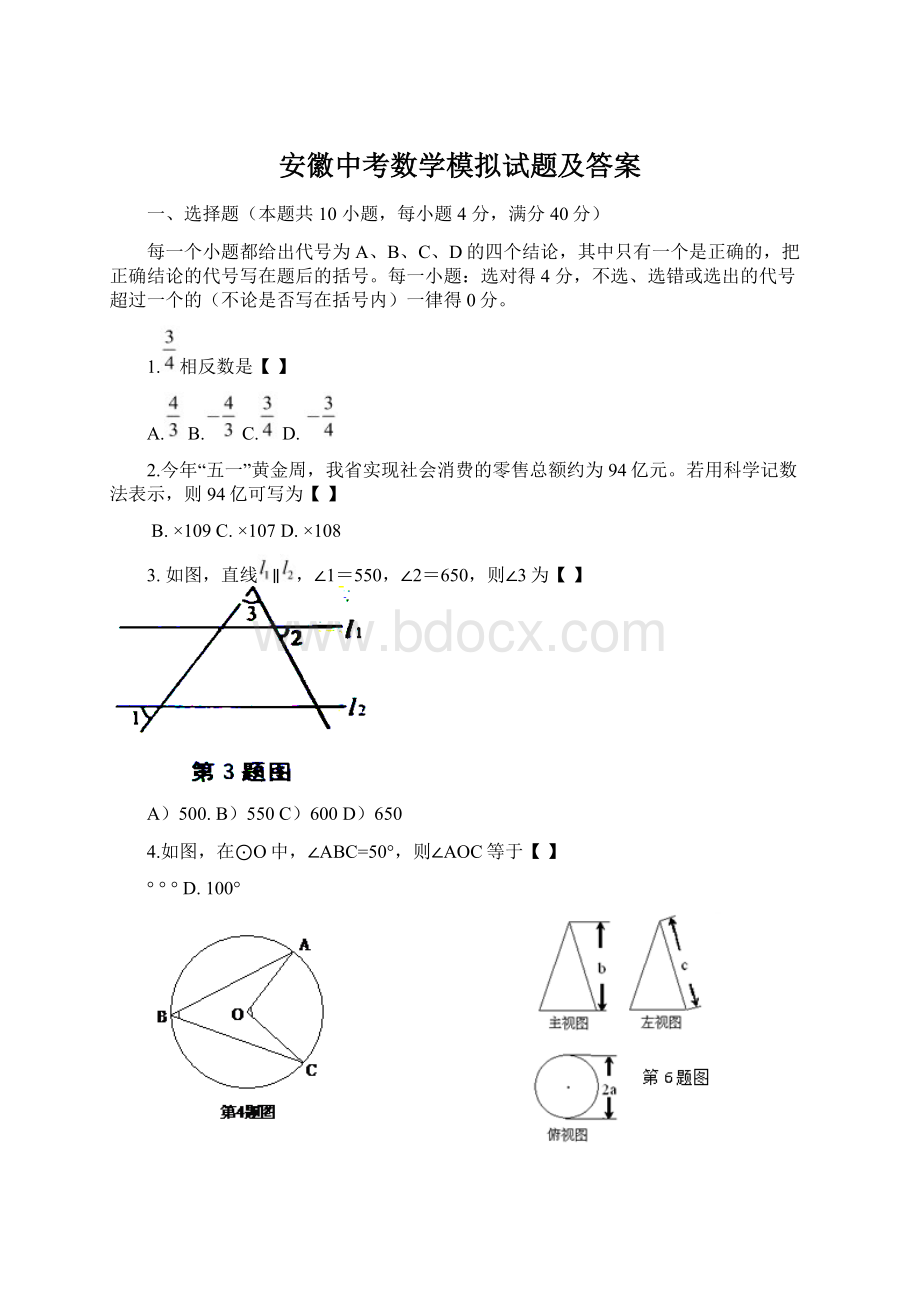
6.如图是某几何体的三视图及相关数据,则判断正确的是…【】
A.a>cB.b>cC.4a2+b2=c2D.a2+b2=c2
7.如图,已知AB∥CD,AD与BC相交于点P,AB=4,CD=7,AD=10,则AP的长等于【】
8.挂钟分针的长10cm,经过45分钟,它的针尖转过的弧长是【】
A.B.C.D.
9.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是…【】
10.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=【】
B.65°
C.72°
D.75°
二、填空题(本题共4小题,每小题5分,满分20分)
11.不等式组的解集是_______________.
12.如图,已知∠1=100°
,∠2=140°
,那么∠3=______
13.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__________________。
(把所有正确答案的序号都填写在横线上)
①∠BAD=∠ACD②∠BAD=∠CAD,③AB+BD=AC+CD④AB-BD=AC-CD
14.右图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是___________________。
(把下图中正确的立体图形的序号都填在横线上)。
三.(本题共2小题,每小题8分,满分16分)
15.解不等式3x+2>2(x-1),并将解集在数轴上表示出来。
16.小明站在A处放风筝,风筝飞到C处时的线长为20米,这时测得∠CBD=60°
,若牵引底端B离地面米,求此时风筝离地面高度。
(计算结果精确到米,)
四、(本题共2小题,每小题8分,满分16分)
17.某石油进口国这几个月的石油进口量比上个月减少了5%,由于国际油价油价上涨,这个月进口石油的费用反而比上个月增加了14%。
求这个月的石油价格相对上个月的增长率。
18.据报道,我省农作物秸杆的资源巨大,但合理利用量十分有限,2006年的利用率只有30%,大部分秸杆被直接焚烧了,假定我省每年产出的农作物秸杆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率。
(取≈
五、(本题共2小题,每小题10分,满分20分)
19.如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°
和60°
,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取≈,计算结果保留整数)
20.如图,DE分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等。
设BC=a,AC=b,AB=c。
⑴求AE和BD的长;
⑵若∠BAC=90°
,△ABC的面积为S,求证:
S=AE·
BD
六、(本题满分12分)
21.杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,如图。
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功请说明理由。
七、(本题满分12分)
22.如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°
,求证:
△ABR≌△CRD;
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件
八、(本题满分14分)
23.按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(Ⅰ)新数据都在60~100(含60和100)之间;
(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:
当p=时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>
0)将数据进行变换,请写出一个满足上述要求的这种关系式。
(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
C
A
二.填空题(本题共4小题,每小题5分,满分20分)
11、2<
x<
=4 12、60°
13、2、3、4 14、1、2、4
三.(本题共2小题,每小题8分,满分16分)
15、解:
原不等式可化为:
…2分
3x+2>
2x-2.
解得x>
-4.…6分
∴原不等式的解集为x>
-4.
在数轴上表示如下:
…8分
16、解:
在Rt△BCD中,CD=BC×
sin60=20×
……6分
又DE=AB=
∴CE=CD+DE=CD+AB=(米)
答:
此时风筝离地面的高度约是米。
………8分
四、(本题共2小题,每小题8分,共16分)
17、解:
设这个月的石油价格相对上个月的增长率为x。
根据题意得
(1+x)(1-5%)=1+14%……5分
解得x=20%答这个月的石油价格相对上个月的增长率为20%.……8分
18、解:
设我省每年产出的农作物秸杆总量为a,合理利用量的增长率是x,由题意得:
30%a(1+x)2=60%a,即(1+x)2=2…………5分
∴x1≈,x2≈-(不合题意舍去)。
……7分
∴x≈。
即我省每年秸秆合理利用量的增长率约为41%。
19.解:
∵AB=8,BE=15,∴AE=23,在Rt△AED中,∠DAE=45°
…4分
∴DE=AE=23.
在Rt△BEC中,∠CBE=60°
∴CE=BE·
tan60°
=,
∴CD=CE-DE=-23≈≈3…10分
即这块广告牌的高度约为3米。
20.解:
(1)∵△ABD与△ACD的周长相等,BC=a,AC=b,AB=c,
∴AB+BD=AC+CD=。
∴BD=;
同理AE=…4分
(2)∵∠BAC=90°
,∴a2+b2=c2,S=…6分
由
(1)知AE·
BD=×
==
即S=AE·
BD…10分
21.解:
(1)=……5分
∵,∴函数的最大值是。
演员弹跳的最大高度是米。
(2)当x=4时,==BC,所以这次表演成功。
……12分
七、(本题满分12分)
22.
(1)证明:
∵∠ABD=90°
,AB∥CR,∴CR⊥BD∵BC=CD,
∴∠BCR=∠DCR…2分
∵四边形ABCR是平行四边形,∴∠BCR=∠BAR∴∠BAR=∠DCR…4分
又∵AB=CR,AR=BC=CD,∴△ABR≌△CRD…6分
(2)由PS∥QR,PS∥RD知,点R在QD上,故BC∥AD。
……8分
又由AB=CD知∠A=∠CDA因为SR∥PQ∥BA,所以∠SRD=∠A=∠CDA,从而SR=SD。
…9分
由PS∥BC及BC=CD知SP=SD。
而SP=DR,所以SR=SD=RD故∠CDA=60°
。
…11分
因此四边形ABCD还应满足BC∥AD,∠CDA=60°
(注:
若推出的条件为BC∥AD,∠BAD=60°
或BC∥AD,∠BCD=120°
等亦可。
)
23.
(1)当P=时,y=x+,即y=。
∴y随着x的增大而增大,即P=时,满足条件(Ⅱ)……3分
又当x=20时,y==100。
而原数据都在20~100之间,所以新数据都在60~100之间,即满足条件(Ⅰ),综上可知,当P=时,这种变换满足要求;
(2)本题是开放性问题,答案不唯一。
若所给出的关系式满足:
(a)h≤20;
(b)若x=20,100时,y的对应值m,n能落在60~100之间,则这样的关系式都符合要求。
如取h=20,y=,……8分
∵a>0,∴当20≤x≤100时,y随着x的增大…10分
令x=20,y=60,得k=60 ①
令x=100,y=100,得a×
802+k=100②
由①②解得,∴。
………14分;