版数学浙江省学业水平考试专题复习选修21 3Word文档格式.docx

版数学浙江省学业水平考试专题复习选修21 3Word文档格式.docx

《版数学浙江省学业水平考试专题复习选修21 3Word文档格式.docx》由会员分享，可在线阅读，更多相关《版数学浙江省学业水平考试专题复习选修21 3Word文档格式.docx（10页珍藏版）》请在冰豆网上搜索。

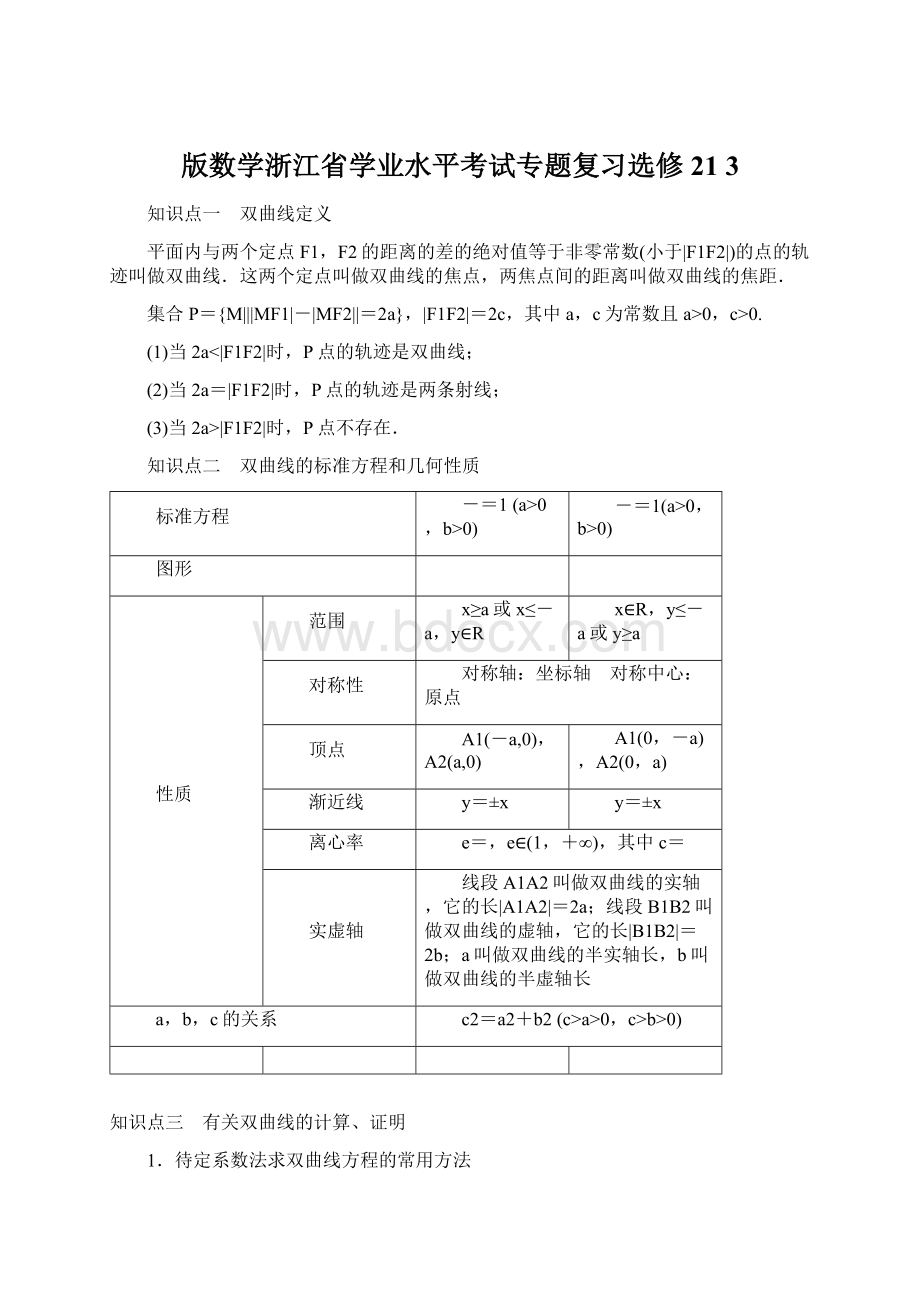
坐标轴　对称中心：

原点

顶点

A1（－a,0），A2（a,0）

A1（0，－a），A2（0，a）

渐近线

y＝±

x

离心率

e＝，e∈（1，＋∞），其中c＝

实虚轴

线段A1A2叫做双曲线的实轴，它的长|A1A2|＝2a；

线段B1B2叫做双曲线的虚轴，它的长|B1B2|＝2b；

a叫做双曲线的半实轴长，b叫做双曲线的半虚轴长

a，b，c的关系

c2＝a2＋b2（c>

a>

b>

知识点三　有关双曲线的计算、证明

1．待定系数法求双曲线方程的常用方法

与双曲线－＝1共渐近线的可设为－＝λ（λ≠0）；

若渐近线方程为y＝±

x，则可设为－＝λ（λ≠0）；

若过两个已知点则设为＋＝1（mn<

0）．

2．等轴双曲线的离心率与渐近线关系

双曲线为等轴双曲线⇔双曲线的离心率e＝⇔双曲线的两条渐近线互相垂直（位置关系）．

3．双曲线的焦点到渐近线的距离等于半虚轴长b.

4．渐近线与离心率

0）的一条渐近线的斜率为

＝＝＝.

题型一　双曲线的定义

例1　已知双曲线x2－＝1的两个焦点为F1，F2，P为双曲线右支上的一点．若|PF1|＝|PF2|，则△F1PF2的面积为（　　）

A．48B．24

C．12D．6

答案　B

解析　由双曲线的定义可得

|PF1|－|PF2|＝|PF2|＝2a＝2，

解得|PF2|＝6，故|PF1|＝8，又|F1F2|＝10，

由勾股定理可知△PF1F2为直角三角形，

因此＝|PF1|×

|PF2|＝24.

感悟与点拨　利用双曲线的定义时，要特别注意条件“差的绝对值”，弄清研究对象是整条双曲线，还是双曲线的一支．

跟踪训练1　

（1）已知圆C1：

（x＋3）2＋y2＝1和圆C2：

（x－3）2＋y2＝9，动圆M同时与圆C1及圆C2相外切，则动圆圆心M的轨迹方程为________________．

（2）设过双曲线x2－y2＝9左焦点F1的直线交双曲线的左支于点P，Q，F2为双曲线的右焦点．若|PQ|＝7，则△F2PQ的周长为________．

答案　

（1）x2－＝1（x≤－1）　

（2）26

解析　

（1）如图所示，设动圆M与圆C1及圆C2分别外切于点A和B.

根据两圆外切的条件，

得|MC1|－|AC1|＝|MA|，

|MC2|－|BC2|＝|MB|，

∵|MA|＝|MB|，

∴|MC1|－|AC1|＝|MC2|－|BC2|，

即|MC2|－|MC1|＝|BC2|－|AC1|＝2<

6，

∴点M到两定点C1，C2的距离的差是常数且小于|C1C2|.

又根据双曲线的定义，得动点M的轨迹为双曲线的左支（点M与C2的距离大，与C1的距离小），

其中a＝1，c＝3，则b2＝8.

故点M的轨迹方程为x2－＝1（x≤－1）．

（2）如图，由双曲线的定义可得

将两式相加得|PF2|＋|QF2|－|PQ|＝4a，

∴△F2PQ的周长为

|PF2|＋|QF2|＋|PQ|

＝4a＋|PQ|＋|PQ|＝4×

3＋2×

7＝26.

题型二　求双曲线的标准方程

例2　

（1）已知双曲线C：

－＝1的离心率e＝，且其右焦点为F2（5,0），则双曲线C的标准方程为（　　）

A.－＝1B.－＝1

C.－＝1D.－＝1

（2）已知双曲线过点（4，），且渐近线方程为y＝±

x，则该双曲线的标准方程为________．

答案　

（1）C　

（2）－y2＝1

解析　

（1）由焦点F2（5,0）知c＝5，

又e＝＝，得a＝4，b2＝c2－a2＝9，

∴双曲线C的标准方程为－＝1.

（2）∵双曲线的渐近线方程为y＝±

x，

∴可设双曲线的方程为x2－4y2＝λ（λ≠0）．

∵双曲线过点（4，），

∴λ＝16－4×

（）2＝4，

∴双曲线的标准方程为－y2＝1.

感悟与点拨　求双曲线的标准方程常用待定系数法．待定系数法的具体过程是先定形，再定量，即先确定双曲线标准方程的形式，再根据a，b，c，e及渐近线之间的关系，求出a，b的值．如果已知双曲线的渐近线方程，求双曲线的标准方程，可利用有公共渐近线的双曲线方程为－＝λ（λ≠0），再由条件求出λ的值即可．

跟踪训练2　

（1）已知双曲线－＝1（a>

0）和椭圆＋＝1有相同的焦点，且双曲线的离心率是椭圆离心率的2倍，则双曲线的标准方程为________．

（2）与双曲线x2－2y2＝2有公共渐近线，且过点M（2，－2）的双曲线的标准方程为________．

答案　

（1）－＝1　

（2）－＝1

解析　

（1）椭圆＋＝1的焦点为F1（－，0），F2（，0），离心率为e＝.

由于双曲线－＝1与椭圆＋＝1有相同的焦点，

∴a2＋b2＝7.

又双曲线的离心率e＝＝，

∴＝＝，

∴a＝2，b2＝c2－a2＝3，

故双曲线的标准方程为－＝1.

（2）x2－2y2＝2化为标准方程得－y2＝1，

设与双曲线－y2＝1有公共渐近线的双曲线方程为

－y2＝k（k≠0），

将点（2，－2）代入得k＝－（－2）2＝－2.

∴双曲线的标准方程为－＝1.

题型三　双曲线的几何性质

例3　

（1）（2017年4月学考）过双曲线－＝1（a>

0）的左顶点A作倾斜角为45°

的直线l，l交y轴于点B，交双曲线的一条渐近线于点C，若＝，则该双曲线的离心率为（　　）

A．5B.

C.D.

（2）设双曲线－＝1（a>

0）的右焦点是F，左、右顶点分别是A1，A2，过F作A1A2的垂线与双曲线交于B，C两点．若A1B⊥A2C，则该双曲线的渐近线方程为________．

答案　

（1）B　

（2）x±

y＝0

解析　

（1）由题意可知，设双曲线的右顶点为D，连接CD，由题意可知，|OA|＝|OB|＝|OD|＝a，

OB是△ADC的中位线，则|CD|＝2a，

则C（a,2a），

将C代入双曲线的渐近线方程y＝x，

整理得，b＝2a，

则该双曲线的离心率e＝＝＝，

∴双曲线的离心率为，故选B.

（2）由题设易知A1（－a,0），A2（a,0），B，C，

因为A1B⊥A2C，所以·

＝－1，整理得a＝b.

因此该双曲线的渐近线方程为y＝±

x，即x±

y＝0.

感悟与点拨　双曲线的几何性质的常考题型为求双曲线的渐近线和离心率．

（1）对于双曲线的渐近线问题，注意公式中双曲线的焦点所在的坐标轴，当焦点在x轴上时，渐近线方程为y＝±

x.当焦点在y轴上时，渐近线方程为y＝±

x.

（2）对于双曲线的离心率问题，根据条件，建立关于a，b，c的齐次方程（或不等式），然后求解即可．

跟踪训练3　

（1）（2018年4月学考）双曲线x2－＝1的渐近线方程是（　　）

A．y＝±

xB．y＝±

C．y＝±

xD．y＝±

3x

（2）设双曲线－＝1（b＞a＞0）的焦距为2c，直线l过A（a,0），B（0，b）两点，已知原点到直线l的距离为c，则双曲线的离心率为________．

答案　

（1）C　

（2）2

解析　

（2）过点O作AB的垂线，垂足为E，

如图所示，在△OAB中，

|OA|＝a，|OB|＝b，|OE|＝c，

|AB|＝＝c.

因为|AB|·

|OE|＝|OA|·

|OB|，

所以c·

c＝ab，即（a2＋b2）＝ab，

两边同除以a2，得2－＋＝0，

解得＝或＝（舍去），

所以e＝＝＝＝2.

一、选择题

1．（2018年6月学考）双曲线－＝1的焦点坐标是（　　）

A．（－5,0），（5,0）B．（0，－5），（0,5）

C．（－，0），（，0）D．（0，－），（0，）

答案　A

2．已知双曲线－y2＝1的焦点坐标为（2,0），则此双曲线的渐近线方程是（　　）

答案　C

解析　由题意可知＝2，

∴a＝±

，

∴双曲线的渐近线方程为y＝±

x＝±

3．若双曲线－＝1上点P到点（5,0）的距离为15，则点P到点（－5,0）的距离为（　　）

A．7B．23

C．5或25D．7或23

答案　D

解析　∵双曲线－＝1，

∴2a＝8，（5,0），（－5,0）是双曲线的两个焦点，

∵点P在双曲线上，∴||PF1|－|PF2||＝8，

∵点P到点（5,0）的距离为15，

∴点P到点（－5,0）的距离是15＋8＝23或15－8＝7.

4．已知双曲线－＝1（a>

0）的实轴长、虚轴长、焦距长成等差数列，则双曲线的渐近线方程为（　　）

解析　由题意可知实轴长为2a，虚轴长为4，焦距长为2，

因为实轴长、虚轴长、焦距长成等差数列，

则2a＋2＝8，解得a＝，

因此双曲线的方程为－＝1，

则双曲线的渐近线方程为y＝±

5．设双曲线＋＝1的渐近线方程为3x±

2y＝0，则a的值为（　　）

A．－4B．－3C．2D．1

解析　因为方程表示双曲线，所以a<

0，

标准方程为－＝1，

所以渐近线方程为y＝±

x，

所以＝，解得a＝－4.

6．若双曲线过点（m，n）（m>

n>

0）且渐近线方程为y＝±

x，则双曲线的焦点（　　）

A．在x轴上B．在y轴上

C．在x轴或y轴上D．无法判断

解析　因为m>

0，所以点（m，n）在第一象限且在直线y＝x的下方，故焦点在x轴上．

7．（2016年10月学考）设双曲线－＝1（a>

0）的左、右焦点分别为F1，F2，以F1为圆心，|F1F2|为半径的圆与双曲线在第一、二象限内依次交于A，B两点，若|F1B|＝3|F2A|，则该双曲线的离心率是（　　）

A.B.C.D．2

解析　由题意知|F1B|＝|F1A|＝2c，

|AF2|＝2c－2a，

已知|F1B|＝2c＝3|AF2|＝6c－6a，即4c＝6a，

得e＝＝.

8．若双曲线－＝1（a>

0）的焦点到其渐近线的距离等于实轴长，则该双曲线的离心率为（　　）

A.B．5C.D．2

解析　焦点（c,0）到渐近线y＝x的距离为＝2a，解得b＝2a.

又a2＋b2＝c2，∴5a2＝c2，

∴离心率e＝＝.

9．设直线l过双曲线C的一个焦点，且与C的一条对称轴垂直，l与C交于A，B两点，|AB|为C的实轴长的2倍，则C的离心率为（　　）

A.B.C．2D．3

解析　设双曲线的标准方程为－＝1（a>

0），

由于直线l过双曲线的焦点且与对称轴垂直，因此直线l的方程为x＝c或x＝－c，

代入－＝1，

得y2＝b2＝，

∴y＝±

，故|AB|＝.

依题意，得＝4a，

∴＝2，∴＝e2－1＝2，∴e＝.

10．已知F1，F2分别是双曲线－＝1（a>

0）的左、右焦点，l1，l2为双曲线的两条渐近线，设过点M（b,0）且平行于l1的直线交l2于点P.若PF1⊥PF2，则该双曲线的离心率为（　　）